TDOA/FDOA estimation algorithm for linear frequency modulated signals
-
摘要: 提出了一种新的快速估计线性调频信号时/频差的算法.该算法将抽取的自模糊函数与Radon变换结合估计线性调频信号的调频率, 通过分数阶傅里叶变换估计出模糊函数脊线与频率轴交点位置, 应用解调频沿脊线搜索模糊函数峰值.对于接收信号中存在多分量的情况, 根据其模糊函数脊线位置的不同, 该算法能够分辨各分量信号, 并分别精确估计出各分量的时/频差.由于只需一维搜索模糊函数峰值, 并可用快速傅里叶变换实现, 该算法大大减少了运算量.仿真实验表明, 随着信噪比的提高, 该算法估计的时/频差均方误差逐渐逼近克拉美-罗下界.Abstract: A novel efficient algorithm for time difference of arrival (TDOA) and frequency difference of arrival (FDOA) estimation between two linear frequency modulated (LFM) signals is proposed in this paper. The proposed approach combines decimated ambiguity function and Radon transform to estimate the chirp rate of the LFM signal; then fractional Fourier transform (FrFT) is used to estimate the point of intersection between the ridge and Doppler axis; finally the peak of ambiguity function is searched efficiently along the ridge by using of dechirping. For the multi-component LFM signal, since different LFM signals have different ridges, the proposed approach can successfully distinguish each LFM signal from the received signal, and both the TDOA and FDOA of each LFM signal can be estimated precisely. Due to fast Fourier transform-based processing and the use of only one-dimensional searches, the proposed approach is computationally efficient. Simulation results show that with the increase of signal noise ratio (SNR), the variances of the estimates are gradually close to the Cramer-Rao lower bound.
-
引言
两路信号间的时延差和多普勒频差的估计是信号处理的基本问题之一, 在目标定位和跟踪等领域有重要应用[1-4].线性调频(Linear Frequency Modulated, LFM)信号是雷达中常见的发射信号[5-7], 研究LFM信号的时/频差快速精确估计对雷达辐射源的精确定位有着重要意义.
常用的时/频差估计方法主要基于模糊函数[8-10].模糊函数的峰值位置对应真实的时/频差, 然而二维搜索模糊函数的峰值, 需要巨大的运算量, 难以满足实时处理的要求.为此, Stein在文献[8]中提出了先粗估计再精估计的算法, 并给出了连续信号时/频差估计的克拉美-罗界.根据现实中多普勒频率远小于采样频率这一信息, 文献[9]采用滤波抽取的方法将模糊函数计算区域限定在感兴趣的区域, 避免了计算完整的模糊函数.根据LFM信号模糊函数存在一条过峰值的脊线的特点, Sharif在文献[10]中提出了沿着模糊函数脊线方向搜索峰值的算法, 但是其对调频率的估计需要计算完整的模糊函数, 并且其在沿脊线搜索的过程中采用逐点搜索, 运算量较大.文献[11]提出了抽取的模糊函数, 并给出了基于二维快速傅里叶变换(Fast Fourier Transform, FFT)的快速算法, 它保留了模糊函数的轮廓, 但不能保证模糊函数真实峰值在抽取后的点阵上, 因而不能有效估计时/频差.
分数阶傅里叶变换(Fractional Fourier Transform, FrFT)作为傅里叶变换的推广, 处理LFM信号具有天然的优势, 目前广泛应用于LFM信号的检测和参数估计[12-15].一个LFM信号在适当的分数阶傅里叶变换域上为一个冲击函数, 表现为LFM信号在该阶上的能量聚集性.由于信号的时延和频移会引起其分数域上幅度谱的平移, 文献[16]通过在不同分数域上模相关, 提出了一种基于FrFT的时/频差联合估计算法.然而, 该算法由于采用模相关, 在低信噪比下, 当变换阶次非最优阶时, 估计效果不佳.
为了实现时/频差的快速精确估计, 本文提出了一种沿脊线快速搜索峰值的算法.首先, 联合Radon变换和抽取的模糊函数快速估计调频率, 并且利用FrFT精确估计出模糊函数脊线与频率轴交点.在沿脊线搜索峰值时, 应用解调频将逐点搜索转化为一次相关, 由相关峰的位置估计出时/频差.该方法能快速实现模糊函数的一维峰值搜索过程, 并能精确分辨出多分量LFM信号.
1 信号模型
假设y1(t)为第一路接收信号, 由单分量LFM信号s(t)和噪声ω1(t)构成, y2(t)为第二路接收信号, 包含了R个分量信号和噪声ω2(t)为
{y1(t)=s(t)+ω1(t)y2(t)=R∑k=1y2,k(t)+ω2(t). (1) 式中:
s(t)=rect(t−T/2T)ej(2πκt+πmt2), (2) rect(t−T/2T)为[0, T]上的门函数, T为信号持续时间, κ为y1(t)的初始频率, m为LFM信号的调频率; ω1(t)和ω2(t)为互不相关的加性白噪声; y2,k(t)=s(t-Δtdk)ej2πΔfdkt为无噪声时y2(t)的第k个分量, k=1, …, R, Δtdk和Δfdk为y2, k(t)相对y1(t)的时差和多普勒频差, 为待估计的参数.
2 抽取的模糊函数与FrFT
2.1 抽取的模糊函数
信号f(t)和g(t)的模糊函数(Ambiguity Function, AF)[8]定义为
χfg(τ,v)=|∫∞−∞f(t)g∗(t−τ)e−j2πvtdt|. (3) 当f(t)=g(t)时, 称χfg(τ, v)为自模糊函数.
信号f(t)和g(t)抽取的模糊函数(Decimated Ambiguity Function, DAF)[11]为两信号模糊函数时间和频率经D倍抽取后的值:
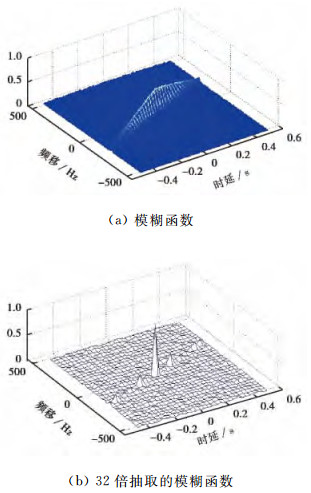
DAFfg(ξ,η)=χfg(ξD,ηD), (4) ξ和η分别为时间和频率D倍抽取后的变量.图 1仿真了LFM信号的模糊函数及抽取的模糊函数, 由仿真图可以看出, LFM信号抽取的模糊函数基本保留了完整模糊函数脊线的位置信息.
2.2 分数阶傅里叶变换
定义信号x(t)在α角度上的FrFT[17]为
Xα(u)=Fα(x(t))=∫∞−∞x(t)Kα(t,u)dt. (5) 式中, Kα(t, u)为核函数,
Kα(t,u)={Aαej(π(u2+t2)cotα−2πutcscα)α≠nπδ(t−u)α=2nπδ(t+u)α=(2n+1)π, (6) α为旋转的角度, Aα=√1−jcotα.我们常用阶数p=2α/π来表示FrFT的角度.
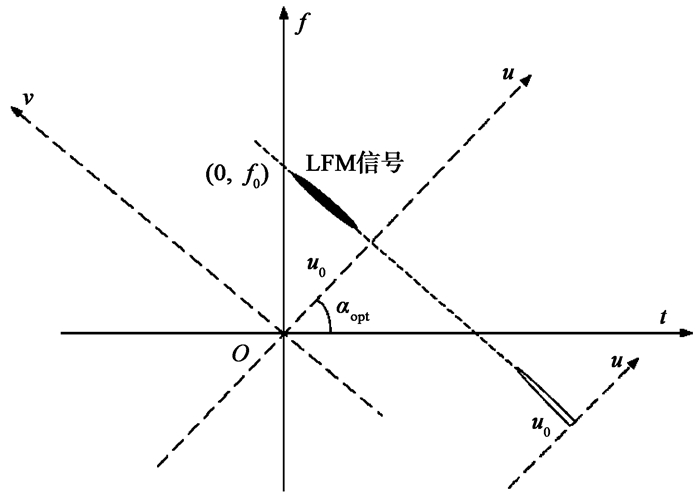
对于一个有限时长的线性调频信号, 其维格纳-威利分布(Wigner-Ville Distribution, WVD)在时频图上呈现为斜刀刃型的分布, 如图 2所示.当角度α垂直于LFM信号时频图的脊线, 即α=-arccot m时, 信号在该分数域上投影出一个峰值, 称该角度α为最优的角度,记为αopt, 对应的阶数称为最优阶,记为popt.对于式(1)中的y1(t), 其初始频率为κ, 在最优阶popt上的峰值位置记为u0, 由图 2中几何关系可知:
κ=u0sin(αopt)=u0/sin(π2popt). (7) 对于y2(t), 各分量的初始频率f0k分别为
f0k=κ+Δfdk−mΔtdk, (8) 与式(7)类似, 同样可得
f0k=u0k/sin(π2popt). (9) 3 LFM信号快速时/频差估计
3.1 联合抽取的模糊函数与Radon变换估计调频率
Radon-Ambiguity变换(Radon-Ambiguity Transform, RAT)[18]常用于LFM信号的检测和估计, 其定义为
R(θ)=∫∞−∞χff(τ,v)dl=∫∞−∞χff(−lsinθ,lcosθ)dl. (10) 式中, χff(τ, v)为信号f(t)的自模糊函数.当f(t)为LFM信号时, χff(τ, v)的脊为过原点的一条直线, 此时只需要对R(θ)进行一维峰值搜索即可获得调频率的估计, 记最大峰值对应的角度为θmax, 则调频率的估计ˆm=tan(θmax−90∘).RAT需要计算信号的自模糊函数, 在实际情况中, 这往往意味着不小的运算量.由于计算抽取的模糊函数所需的运算量较小[11], 且适当抽取的模糊函数可以保留脊线的主要特性, 因此可结合Radon变换和抽取的模糊函数来代替RAT方法估计LFM信号的调频率.
3.2 利用FrFT估计模糊函数脊线与频率轴交点
第k个分量y2, k(t)与y1(t)的互模糊函数脊线为过峰值点(Δtdk, Δfdk), 斜率为m的直线, 脊线交频率轴于(0, Δfdk-mΔtdk)点.联立2.2节中式(7)、(8)和(9), 可得
fdk−mΔtdk=u0k−u0sin(π2popt). (11) 根据式(11), 由两路信号在最优阶上峰值的位置差u0k-u0即可求解出互模糊函数脊线与频率轴交点坐标.
3.3 利用解调频沿脊线一维搜索模糊函数峰值
在无噪声的环境中, 分别对y1(t)和y2, k(t)乘上e-jπm′t2, 记新的信号分别为y′1(t)和y′2, k(t), 即
y′1(t)=y1(t)exp(−jπm′t2), (12) y′2,k(t)=y1(t−Δtdk)ej2πΔfdke−jπm′t2. (13) 将解调频后的信号代入式(3), 有
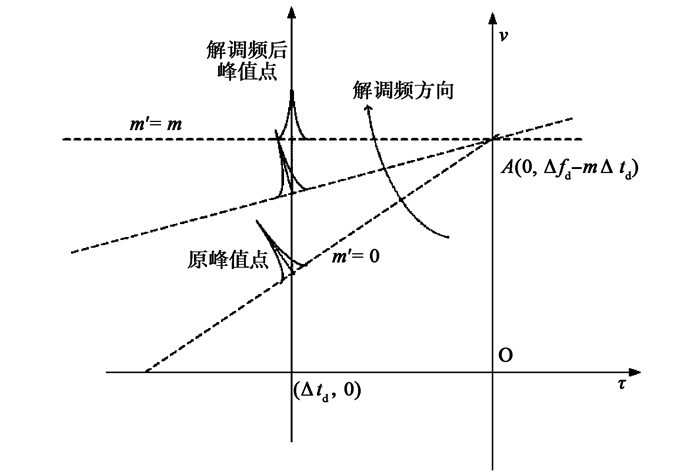
χy′2,ky′1(τ,v)=|∫∞−∞y′2,k(t)y′∗1(t−τ)e−j2πvtdt|=|∫max (14) 可见, 新的模糊函数的脊线方程为
v = \Delta {f_{{\rm{d}}k}} - m'\Delta {t_{{\rm{d}}k}} + \left( {m - m'} \right)\left( {\tau - \Delta {t_{{\rm{d}}k}}} \right), (15) 峰值为(Δtdk, Δfdk-m′Δtdk), 脊线斜率为m-m′.如图 3所示, 当τ=0时, v=Δfdk-mΔtdk, 可见信号解调频后, 新的模糊函数的脊线与频率轴的交点坐标仍为(0, Δfdk-mΔtdk).当m′=m, 即两路信号正确解调频时, 模糊函数的脊线旋转至平行于τ轴, 此时两路信号为频率相差Δfdk-mΔtdk的单频信号, 对信号频率补偿后, 可通过一次时域相关估计出解调频后模糊函数χy′2, ky′1(τ, v)的峰值坐标, 进而估计出y2, k(t)相对y1(t)的时/频差Δtdk和Δfdk.
3.4 多分量信号分辨性能分析
多分量信号间的干扰会降低参数估计的性能.为了抑制多分量的影响, 在估计第k个分量信号的时/频差时, 可对其他分量的最优阶FrFT进行峰值遮隔处理[13], 实现分数阶傅里叶变换域滤波, 再将滤波后的信号逆变换回时域处理.显然, 该方法必须先分辨出各分量信号才能完成以上处理过程, 在本节分析了算法对多分量信号的分辨性能.
式(1)中的各分量信号是LFM信号s(t)经不同时延和频移后的结果, 因此各分量信号具有相同的最优阶.由文献[15]可知, 有限长LFM信号s(t)在最优阶popt的分数阶幅度谱为一个sin c函数, 且有
\begin{array}{l} \left| {S\left( u \right)} \right| = \left| {{F_{{\alpha _{{\rm{opt}}}}}}\left( {s\left( t \right)} \right)} \right|\\ \;\;\;\;\;\;\;\;\; = {A_{{\alpha _{{\rm{opt}}}}}}T\left| {\sin {\rm{c}}\left( {\pi T\csc {\alpha _{{\rm{opt}}}}u} \right)} \right|. \end{array} (16) 根据FrFT的时延和频移性质, 各分量的分数阶幅度谱表现为s(t)分数阶幅度谱|Spopt(u)|的平移, 即
\left| {{Y_{2,k}}\left( u \right)} \right| = \left| {S\left( {u - \Delta {t_{{\rm{d}}k}}\cos {\alpha _{{\rm{opt}}}} - \Delta {f_{{\rm{d}}k}}\sin {\alpha _{{\rm{opt}}}}} \right)} \right|. (17) 当两个分量的最优阶FrFT峰值间隔小于其最优阶幅度谱主瓣3 dB宽度时, 我们就认为分辨出了这两个分量信号.因此, 本方法对多分量信号的分辨率为
\Delta u = \frac{{{\rm{Width}}\left( {\sin {\rm{c}}} \right)}}{{\pi T\left| {\cos {\alpha _{{\rm{opt}}}}} \right|}} \approx \frac{{0.44\left| {\sin {\alpha _{{\rm{opt}}}}} \right|}}{{\pi T}}, (18) Width(sin c)为sin c函数主瓣的3 dB宽度, 约为0.44.
4 仿真实验及分析
4.1 调频率的估计
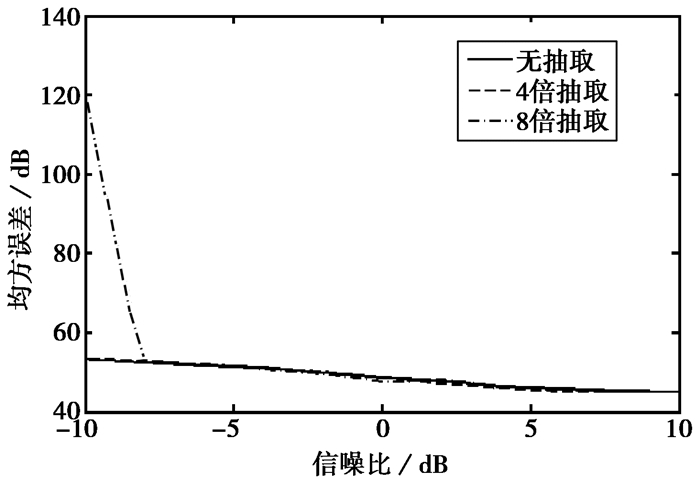
调频率的估计直接影响到时/频差估计的精度, 算法联合Radon变换和抽取的模糊函数来估计调频率, 本节仿真了抽取因子对调频率估计的影响.图 4为不同抽取倍数所估计到的调频率的均方误差, 信号调频率为m=3.125×107 Hz/s.由图 4可以看出, 信噪比为-10 dB时, 无抽取和4倍抽取能够准确估计出调频率, 而8倍抽取获得了错误的估计, 这是因为随着抽取倍数的提高, 抽取的模糊函数脊上的点在减少, Radon变换积累出的峰值能量降低, 更容易湮没在强噪声中.然而, 在信噪比满足三种抽取都能够估计出调频率时, 三者估计出调频率的均方误差基本一致.这说明适当倍数的抽取对调频率估计的影响很小, 本文所提出的联合Radon变换和抽取的模糊函数来估计调频率是可靠的.
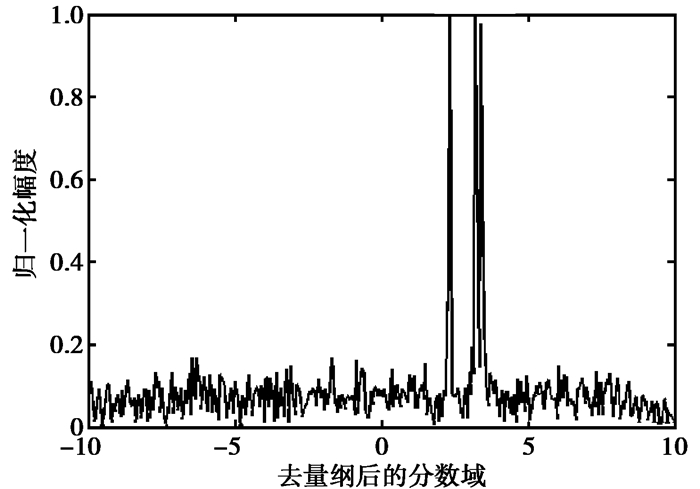
对于多分量信号, 调频率相同导致Radon变换无法将其分辨.由3.4节可知, 多分量LFM信号在最优阶的幅度谱位置不同.由于LFM信号在最优阶表现出能量聚集性, 各分量的峰值主瓣很窄, 且FrFT为线性变换, 多分量信号的FrFT不会产生交叉项干扰, 因此算法对多分量信号具有很强的分辨能力.图 5给出了0 dB信噪比下调频率相同的三分量LFM信号在最优阶FrFT的归一化幅度谱, 从图 5可以清晰分辨出这3个分量信号.
4.2 时/频差的估计
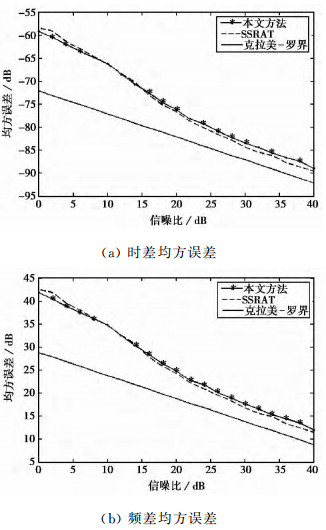
选取LFM信号带宽B=1 MHz, 信号持续时间为80 μs, 调频率m=1.25×1010 Hz/s, y1(t)的初始频率κ=0, 采样率fs=4 MHz, 观测时间为100 μs, 抽取因子D=8.y2(t)为单分量信号, 时频差为(Δtd, Δfd)=(-0.5 μs, -3 200 Hz).图 6仿真了本文方法和文献[10]的单切片RAT(Single Slice Radon Ambiguity Transform, SSRAT)方法对单分量LFM信号时/频差估计的均方误差.可以看出, 两种方法所估计到的时/频差均方误差基本一致, 随着信噪比的提高, 时差和频差的均方误差逐渐逼近克拉美-罗界, 在40 dB信噪比下, 时/频差均方误差比克拉美-罗界高约3 dB.
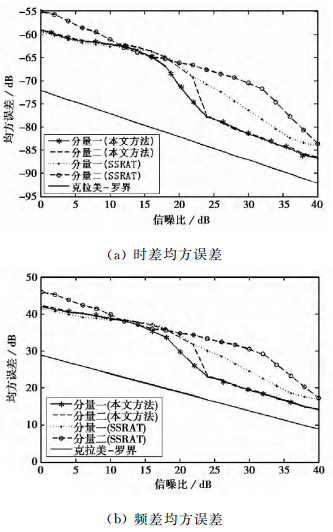
为了检验本算法对多分量信号的时/频差估计效果, 信号y2(t)中除了原有的分量(Δtd, Δfd)=(-0.5 μs, -3 200 Hz)外, 再加入一个调频率相同而时/频差为(1.25 μs, 8 000 Hz)的分量, 其余参数保持不变.
图 7为分别用本文方法和SSRAT方法在以上参数条件下仿真得到的时/频差估计均方误差图.由图 7可以看出, 对于多分量LFM信号的时/频差估计, 本文所提的方法处理要优于SSRAT方法, 这主要是由于本文方法在最优阶分数域对多分量LFM信号进行了分离, 能够有效降低各分量信号间的干扰.
4.3 算法运算量
在调频率已知时, 本文方法只需要计算两路接收信号的最优阶FrFT和一次相关, 由于计算FrFT的运算量与FFT相当[17], 本文方法的运算复杂度为O(Nlog2N).文献[10]中给出的SSRAT算法的运算量, 是在信号调频率已估计到的前提下的运算量, 其计算复杂度为O(N2).
在调频率未知时, SSRAT方法需要先计算信号的自模糊函数, 而本文方法只需要计算信号抽取的自模糊函数.表 1比较了调频率未知时SSRAT算法和本方法的运算量, 抽取因子D=8.从表 1可以看出, 本文提出的算法大幅降低了运算量, 在N=1 000时其运算量仅为SSRAT算法运算量的2.88%, 运算速度明显优于SSRAT算法.
表 1 本文方法和SSRAT方法运算量对比算法 运算量(复乘次数) N=1 000 本文算法 \frac{{3{M^2}}}{{2{D^3}}}log2M+M+9Nlog2N+10N 3.5×105 SSRAT算法 N2log2N+2N2+5Nlog2N 1.2×107 5 结论
针对LFM信号, 提出了一种新的快速估计其时/频差的算法.该算法首先对抽取的自模糊函数做Radon变换估计调频率, 并利用最优阶FrFT估计出模糊函数脊线与频率轴交点, 最后应用解调频沿脊一维搜索模糊函数峰值.由于抽取的模糊函数耗费的运算量较少, 并用一次相关实现沿脊搜索峰值的过程, 算法在运算速度上具有明显优势.本算法能够有效分辨多分量信号, 并分别精确估计出各分量的时/频差.本文给出了算法所需的一些理论推导, 仿真实验验证了本文的结论.
-
表 1 本文方法和SSRAT方法运算量对比
算法 运算量(复乘次数) N=1 000 本文算法 \frac{{3{M^2}}}{{2{D^3}}}log2M+M+9Nlog2N+10N 3.5×105 SSRAT算法 N2log2N+2N2+5Nlog2N 1.2×107 -
[1] 孙正波, 叶尚福.利用互模糊函数实现卫星干扰源定位[J].电波科学学报, 2004, 19(5):525-529. doi: 10.3969/j.issn.1005-0388.2004.05.004 SUN Z B, YE S F.Satellite interference location using cross ambiguity function[J].Chinese journal of radio science, 2004, 19(5):525-529.(in Chinese) doi: 10.3969/j.issn.1005-0388.2004.05.004
[2] 孙正波, 叶尚福.一种时差/频率差快速联合估计方法[J].电波科学学报, 2006, 21(5):641-646. doi: 10.3969/j.issn.1005-0388.2006.05.001 SUN Z B, YE S F.Fast algorithm for joint estimation of DTO and DFO[J].Chinese journal of radio science, 2006, 21(5):641-646.(in Chinese) doi: 10.3969/j.issn.1005-0388.2006.05.001
[3] 曲付勇, 孟祥伟.基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J].电子与信息学报, 2014, 36(5):1075-1081. http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201405010 QU F Y, MENG X W.Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J].Journal of electronics&information technology, 2014, 36(5):1075-1081.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201405010
[4] 李昕.基于双通道DFRFT互谱法的Chirp信号时延估计[J].电子学报, 2014, 42(6):1068-1073. doi: 10.3969/j.issn.0372-2112.2014.06.005 LI X.Time delay estimation of chirp signals based on doubled-channel DFRFT cross-spectrum[J].Acta electronica sinica, 2014, 42(6):1068-1073.(in Chinese) doi: 10.3969/j.issn.0372-2112.2014.06.005
[5] CHEN X L, GUAN J, LIU N B, et al.Maneuvering target detection via radon-fractional Fourier transform-based long-time coherent integration[J].IEEE transactions on signal processing, 2014, 62(4):939-953. doi: 10.1109/TSP.2013.2297682
[6] 朱文涛, 苏涛, 杨涛, 等.线性调频连续波信号检测与参数估计算法[J].电子与信息学报, 2014, 36(3):552-558. http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201403007 ZHU W T, SU T, YANG T, et al.Detection and parameter estimation of linear frequency modulation continuous wave signal[J].Journal of electronics&information technology, 2014, 36(3):552-558.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/dzkxxk201403007
[7] 朱文涛, 苏涛, 杨涛, 等.低信噪比下线性调频连续波信号的参数估计[J].电波科学学报, 2013, 28(6):1158-1164. http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201306024 ZHU W T, SU T, YANG T, et al.Parameter estimation of linear frequency modulated continuous wave signal in low SNR[J].Chinese journal of radio science, 2013, 28(6):1158-1164.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/dbkxxb201306024
[8] STEIN S.Algorithms for ambiguity function processing[J].IEEE transactions on ASSP, 1981, 29(3):588-599. doi: 10.1109/TASSP.1981.1163621
[9] TOLIMIERI R, WINOGRAD S.Computing the ambiguity surface[J].IEEE transactions on ASSP, 1985, 33(4):1239-1245. https://www.researchgate.net/publication/3177873_Computing_the_ambiguity_surface
[10] SHARIF M R, ABEYSEKERA S S.Efficient wideband signal parameter estimation using a radon-ambiguity transform slice[J].IEEE transactions on AES, 2007, 43(2):673-688. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4285361
[11] AUSLANDER L, TOLIMIERI R.Computing decimated finite cross-ambiguity functions[J].IEEE transactions on ASSP, 1988, 36(3):359-364. doi: 10.1109/29.1532
[12] 杜雨洺, 杨建宇.基于FRFT的LFMCW雷达加速动目标检测与参数估计[J].电波科学学报, 2005, 20(6):815-819. doi: 10.3969/j.issn.1005-0388.2005.06.026 DU Y M, YANG J Y.Novel method of moving target detection and parameter estimation for LFMCW radar[J].Chinese journal of radio science, 2005, 20(6):815-819.(in Chinese) doi: 10.3969/j.issn.1005-0388.2005.06.026
[13] 史文国, 徐向辉.基于分数阶傅里叶变换的多分量线性调频信号检测和参数估计的快速自适应方法[J].科学技术与工程, 2012, 12(7):1517-1521. doi: 10.3969/j.issn.1671-1815.2012.07.012 SHI W G, XU X H.Fast adaptive method of the multi-LFM signal detection and parameter estimation based on fractional Fourier transform[J].Science technology and engineering, 2012, 12(7):1517-1521.(in Chinese) doi: 10.3969/j.issn.1671-1815.2012.07.012
[14] 李会勇, 许丁文, 胡进峰, 等.基于FRFT的天波雷达多机动目标检测[J].系统工程与电子技术, 2014, 36(9):1725-1730. http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201409009 LI H Y, XU D W, HU J F, et al.FRFT based algorithm for maneuvering target detection with OTH Radar[J].Systems engineering and electronics, 2014, 36(9):1725-1730.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201409009
[15] 刘锋, 徐会法, 陶然, 等.分数阶Fourier域多分量LFM信号间的分辨研究[J].中国科学(信息科学), 2012, 42(2):136-148. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201202003.htm LIU F, XU H F, TAO R, et al.Research on resolution among multi-component LFM signals in the fractional Fourier domain[J].Science China (information science), 2012, 42(2):136-148.(in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201202003.htm
[16] OONINCX P J.Joint time-frequency offset detection using the fractional fourier transform[J].Signal processing, 2008, 88:2936-2942. doi: 10.1016/j.sigpro.2008.06.017
[17] OZAKTAS H M, ARIKAN O, KUTAY M A, et al.Digtal computation of the fractional Fourier transform[J].IEEE transactions on signal processing, 1996, 44(9):2141-2150. doi: 10.1109/78.536672
[18] WANG M S, CHAN A K, CHUI C K.Linear frequency-modulated signal detection using radon-ambiguity transform[J].IEEE transactions on signal processing, 1998, 46(3):571-586. doi: 10.1109/78.661326
-
期刊类型引用(1)
1. 何其芳,张群,罗迎,梁必帅. 基于k分辨FB级数展开的多分量LFM信号分离. 空军工程大学学报(自然科学版). 2017(04): 60-65 .  百度学术
百度学术
其他类型引用(4)




 下载:
下载: