An iterative method for solving 3D parabolic equation
-
摘要: 为了高效且高精度地求解三维抛物方程(parabolic equation,PE),提出了一种求解三维PE的迭代方法. 该方法采用有限差分(finite difference,FD)近似方法,保留交替方向隐式(alternating direction implicit, ADI)方法的计算模式. 推导了该方法对应的相对误差关系式,在推导过程中考虑计算式分裂项丢失带来的误差影响. 对比现有的求解三维PE的ADI方法(记为ADI-PE)和克兰克·尼科森(Crank-Nicolson)求解方法(记为CN-PE),该方法能够提高计算精准度,且可通过迭代达到一定计算精度. 该方法保留了ADI的计算高效特性,是一种求解三维PE的高效高精准度的方法.
-
关键词:
- 抛物方程(PE) /
- 有限差分(FD)方法 /
- 迭代 /
- 交替方向隐式(ADI) /
- 相对误差
Abstract: To solve 3D parabolic equation efficiently (PE) and accurately, an iterative method for solving 3D PE is proposed. In this method, finite difference (FD) approximation is applied. The proposed method retains the character of the alternating-direction-implicit (ADI) method. The numerical error caused by the split term of the proposed method is considered in the process of derivation. The proposed method can improve the calculation accuracy compared to the ADI-PE method and Crank-Nicolson parabolic equation (CN-PE) method. A certain accuracy can be achieved by several times of iteration. This method is efficient and accurate for solving 3D PE. -
引 言
抛物方程(parabolic equation,PE) 法是预测无线电波传播最常用的方法之一. 该方法能模拟近轴方向,即模拟电磁波传播方向上的圆锥形区域内的电磁波传播. 在远距离传播问题上,PE具有计算高效的特点,且能够同时处理大气结构不均匀和地形不规则引起的折射和绕射效应[1-2] . 求解PE的方法主要有两种:有限差分(finite difference, FD)近似方法[3]和分步傅里叶(split-step Fourier, SSF)方法[4]. 和SSF方法对比,FD方法在处理计算空间内地形边界问题上具有较为灵活的特点,近年来也成为国内外研究者的研究热点.
目前,利用FD方法求解PE的研究中,郭琪等人推导了高阶近似的二维PE求解模型以及适用于不规则地形的高阶模型,并分析了模型所能计算的最大传播仰角和最大的坡度角[5-6]. 此外,郭琪等人[7]还对吸收边界问题进行研究,提出了一种基于全局透射边界条件的宽角PE电波预测模型,该模型提高了PE求解的计算效率. Lytaev等人[8-9]采用非本地边界条件处理计算域的上下边界,提出了一种更高阶的求解二维PE的Numerov-Padé方法,对比SSF方法,该方法能够减少PE所需的计算区域范围,具有一定计算效率与计算稳定性. 利用PE的一些求解方法进行应用分析的研究中,文献[10]采用时域有限差分(finite-difference time-domain, FDTD)和二维单向/双向PE方法,分析了低频短距离高传播角电波传播特性. 王丹丹等人[11]将宽角与窄角PE方法应用到地表低频电波传播的问题研究中,分析了复杂地表参数设置对PE求解精度的影响. 利用三维PE进行高效求解的研究中,Martelly等人[12]提出一种求解三维PE的交替方向隐式(alternating direction implicit, ADI)方法(记为ADI-PE),对比克兰克·尼科森(Crank-Nicolson)求解方法(记为CN-PE)[1],ADI方法具有计算效率高的优势. 何姿等人[13]推导了双向ADI-PE,并将该方法应用在高速公路的实际场景中. 黄璐等人[14]将ADI-PE应用到机场盲降系统中,并提出了更高效的并行算法.
综上所述,近年来国内外研究者在用FD方法求解PE的研究主要集中在二维PE问题,对三维PE问题的研究尚少. 在有关FDTD求解方法的研究中,文献[15]提出了一种迭代方法,该方法能减少ADI-FDTD的计算误差,并保留ADI的高效计算特性. ADI-PE方法是求解三维PE的方法中应用较广泛方法,因此,考虑通过迭代的方式对该方法进行优化具有一定的意义.
本文提出一种求解三维PE的迭代方法,其保留了ADI方法的高效计算模式. 对比现有应用广泛的ADI-PE及 CN-PE方法,该方法能够提高计算精准度、减小误差,且可通过迭代达到一定计算精度.
1 三维PE迭代方法
1.1 求解三维PE的CN-PE与ADI方法
由麦克斯韦方程组推导得到三维直角坐标系下的PE为
∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2=k20n2ψ=0. (1) 式中:
ψ 为水平极化或垂直极化下的电场或磁场;k0 为波数;n为折射率(当为空气时,n=1). 当电波传播方向为x 方向时,引入辅助函数ψ(x,y,z)=u(x,y,z)e−jk0x. (2) 假设
|∂2ψ∂x2|≪k0|∂ψ∂x|, (3) 将式(2)代入式(1)得
∂u∂x=12jk0(∂2u∂y2+∂2u∂z2). (4) 对式(4)中的微分算子进行FD近似,化简得到CN-PE求解方法:
(1−ry4jk0δy−rz4jk0δz)uk+1i,j=(1+ry4jk0δy+rz4jk0δz)uki,j. (5) 式中:
{ry=ΔxΔy2rz=ΔxΔz2; {δyuki,j=uki−1,j−2uki,j+uki+1,jδzuki,j=uki,j−1−2uki,j+uki,j+1. (6) 式(5)的CN-PE方法求解涉及五对角线的稀疏矩阵,求解效率较低. 为提高求解三维PE的效率,研究者提出了求解三维PE的ADI方法[12] ,形式如下:
(1−rz4jk0δz)uk+12i,j=(1+ry4jk0δy)uki,j;(1−ry4jk0δy)uk+1i,j=(1+rz4jk0δz)uk+12i,j. (7) 1.2 三维PE的迭代方法推导
将式(5)改写为以下形式:
(1−ry4jk0δy)(1−rz4jk0δz)uk+1i,j=(1+ry4jk0δy)(1+rz4jk0δz)uki,j−ry4jk0rz4jk0δyδz(uk+1i,j−uki,j). (8) 式(8)等号右边最后一项为ADI-PE方法所丢弃的分裂误差项,其对求解三维PE精准度的影响与网格步进大小有关.
考虑以下关系式:
[M]=(1−ry4jk0δy)(1−rz4jk0δz); (9) P=(1+ry4jk0δy+rz4jk0δz)uki,j; (10) [N]=ry4jk0rz4jk0δyδz. (11) 根据式(9)~(11),式(8)可以写为
[M]uk+1=[N]uk+1+P. (12) 该式具有以下线性求解模式:
[M]uk+1n+1=[N]uk+1n+P. (13) 将式(9)~(11)代入式(13)中,可得
(1−ry4jk0δy)(1−rz4jk0δz)uk+1n+1=(1+ry4jk0δy)(1+rz4jk0δz)uk+1−ry4jk0rz4jk0δyδz(uk+1n+1−uk+1). (14) 式(14)分裂成两步得到求解三维PE迭代方法的计算式:
(1−ry4jk0δy)utmpn+1=(1+rz4jk0δz)uk−12(ry4jk0rz4jk0δyδz)(uk+1n−uk);(1−rz4jk0δz)uk+1n+1=(1+ry4jk0δy)utmp−12(ry4jk0rz4jk0δyδz)(uk+1n−uk). (15) 观察式(15)可知,其计算式子保留了ADI高效的求解模式,可有效快速求解三维PE.
1.3 误差分析
本节推导所提出的三维PE迭代方法的误差关系式. 亥姆霍兹波动方程的精确解为
ψ(x,y,z)=Ae−j(kxx+kyy+kzz). (16) 式中,A为常量.
u(x,y,z) 表示为u(x,y,z)=Aekxx+kyy+(kz−k0)z. (17) 将式(17)代入到不同PE求解方法中,归一化波数得到
ˉk0 ,不同方向上的波矢分量为{ˉkx=ˉk0cosφsinθˉky=ˉk0sinφsinθˉkz=ˉk0cosθ. (18) 将式(18)代入到式(15)可得所提出的求解三维PE迭代方法的相对误差关系式为:
ejˉk0,1λ(1−cosθ)απN2=1+jαsin2ˉk0λsinφsinθ2N1+jαsin2ˉk0λcosφsinθ2N−(12α2sin2ˉk0λsinφsinθ2Nsin2ˉk0λcosφsinθ2N)(Fn−1−1)(1+jαsin2ˉk0λcosφsinθ2N);ejˉk0,2λ(1−cosθ)απN2=1+jαsin2ˉk0λcosφsinθ2N1+jαsin2ˉk0λsinφsinθ2N−(12α2sin2ˉk0λsinφsinθ2Nsin2ˉk0λcosφsinθ2N)(Fn−1−1)(1+jαsin2ˉk0λsinφsinθ2N). (19) 式中:
α=Δx/(k0Δz2) ,Δz=Δy ;N=λ/Δz=2π/(k0Δz) ;Fn−1 为上一迭代式右端结果.2 仿真结果
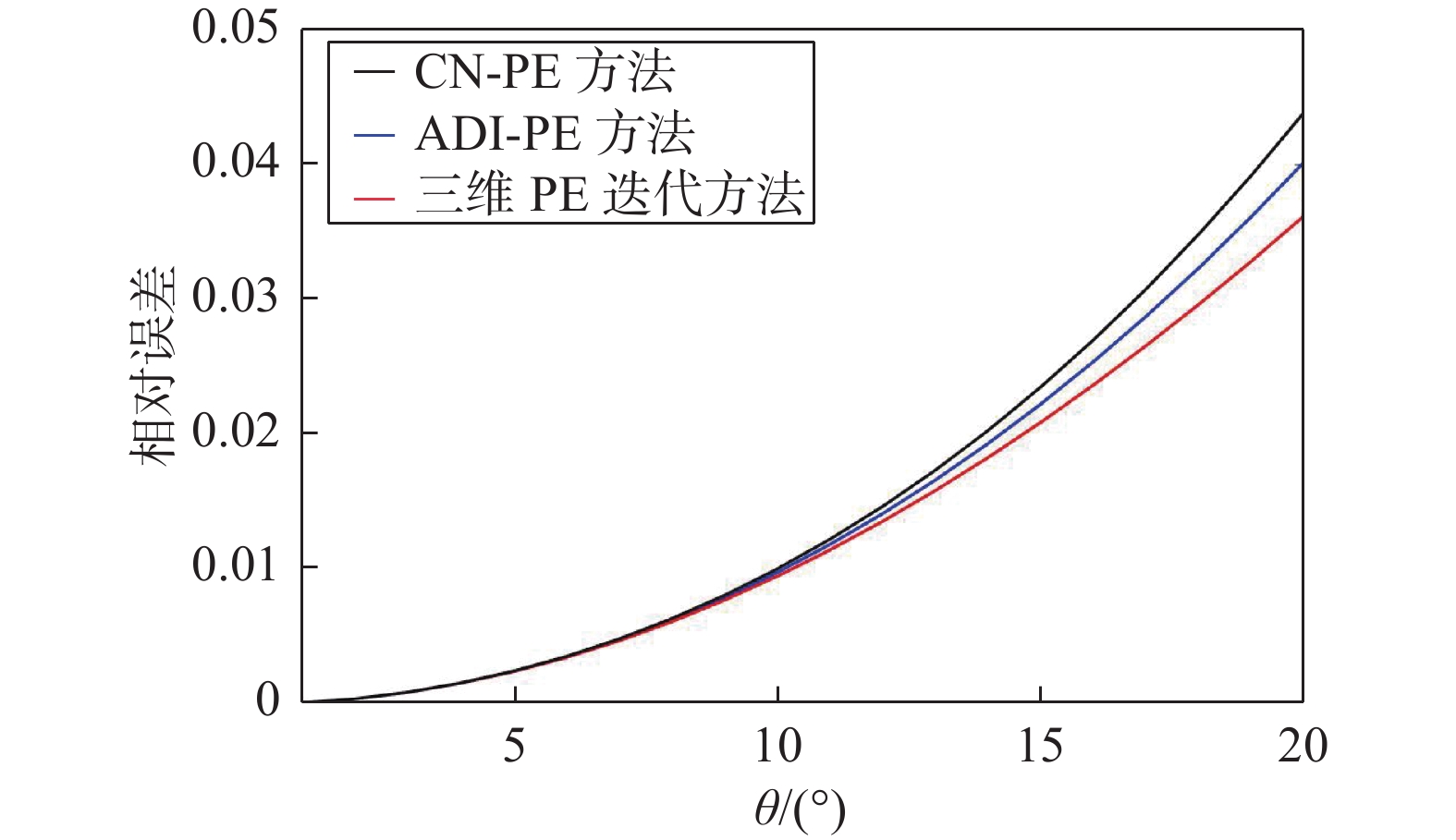
将本文所提求解三维PE的迭代方法与CN-PE方法、ADI-PE方法性能进行对比. 当与网格步进 大小相关的系数
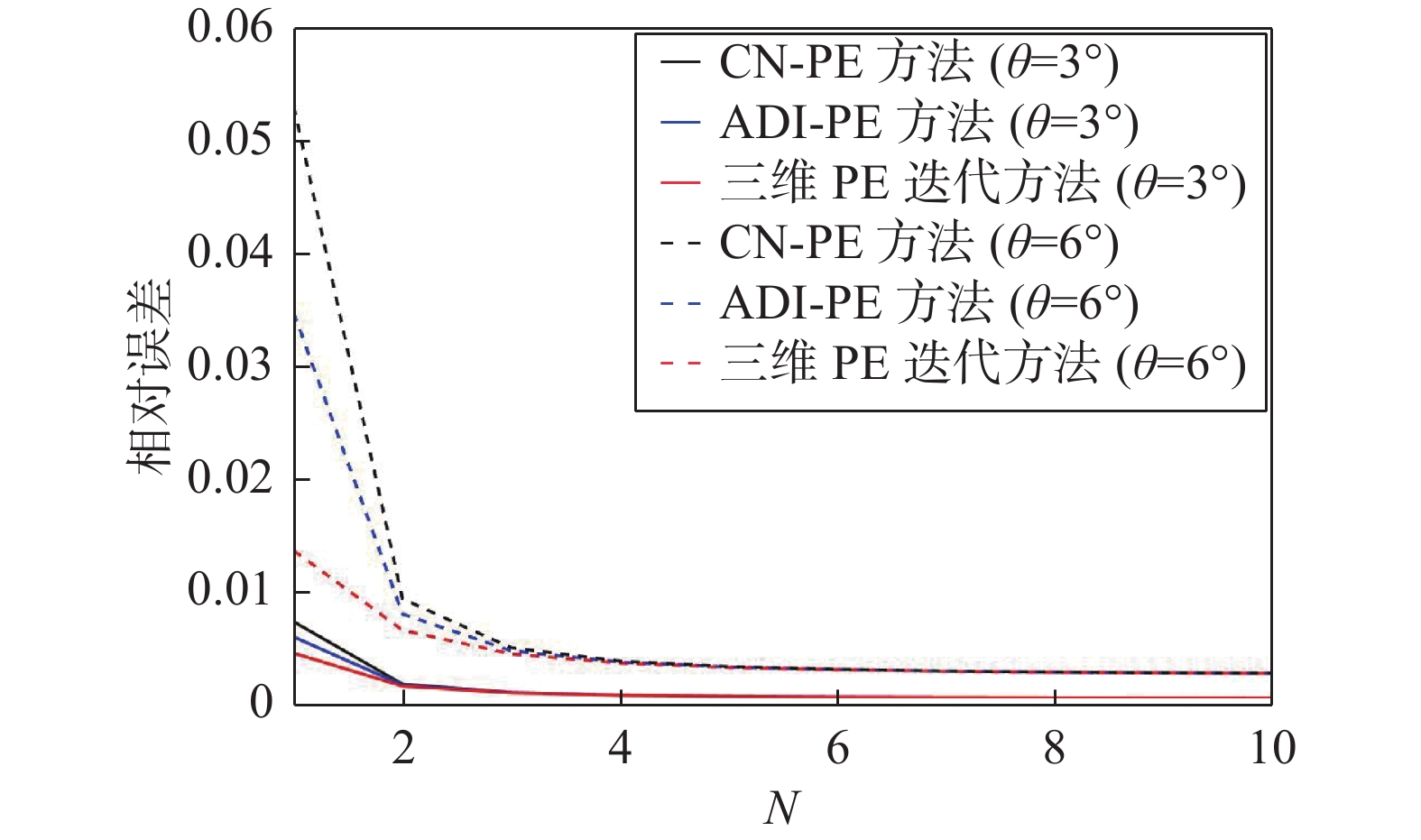
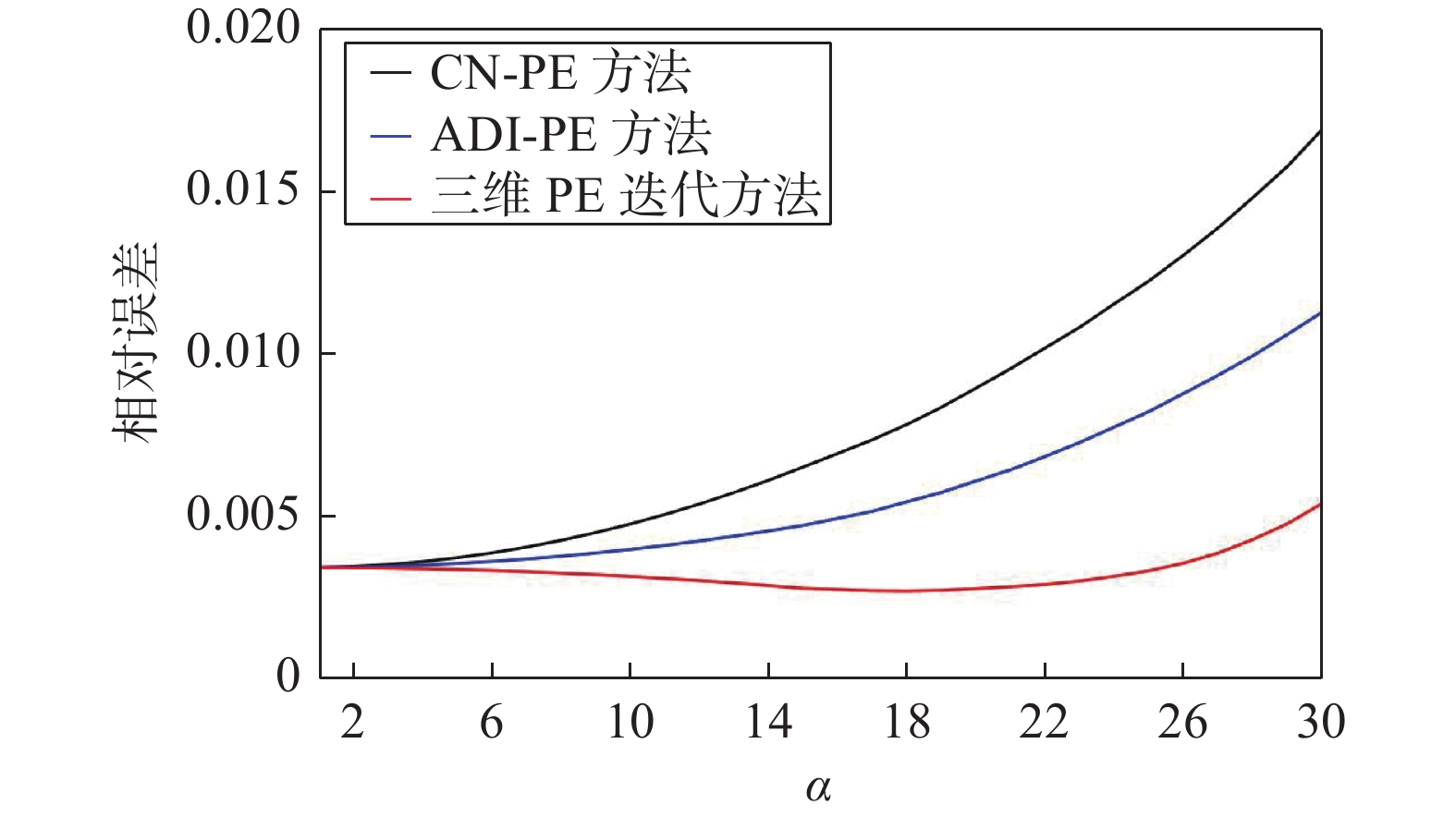
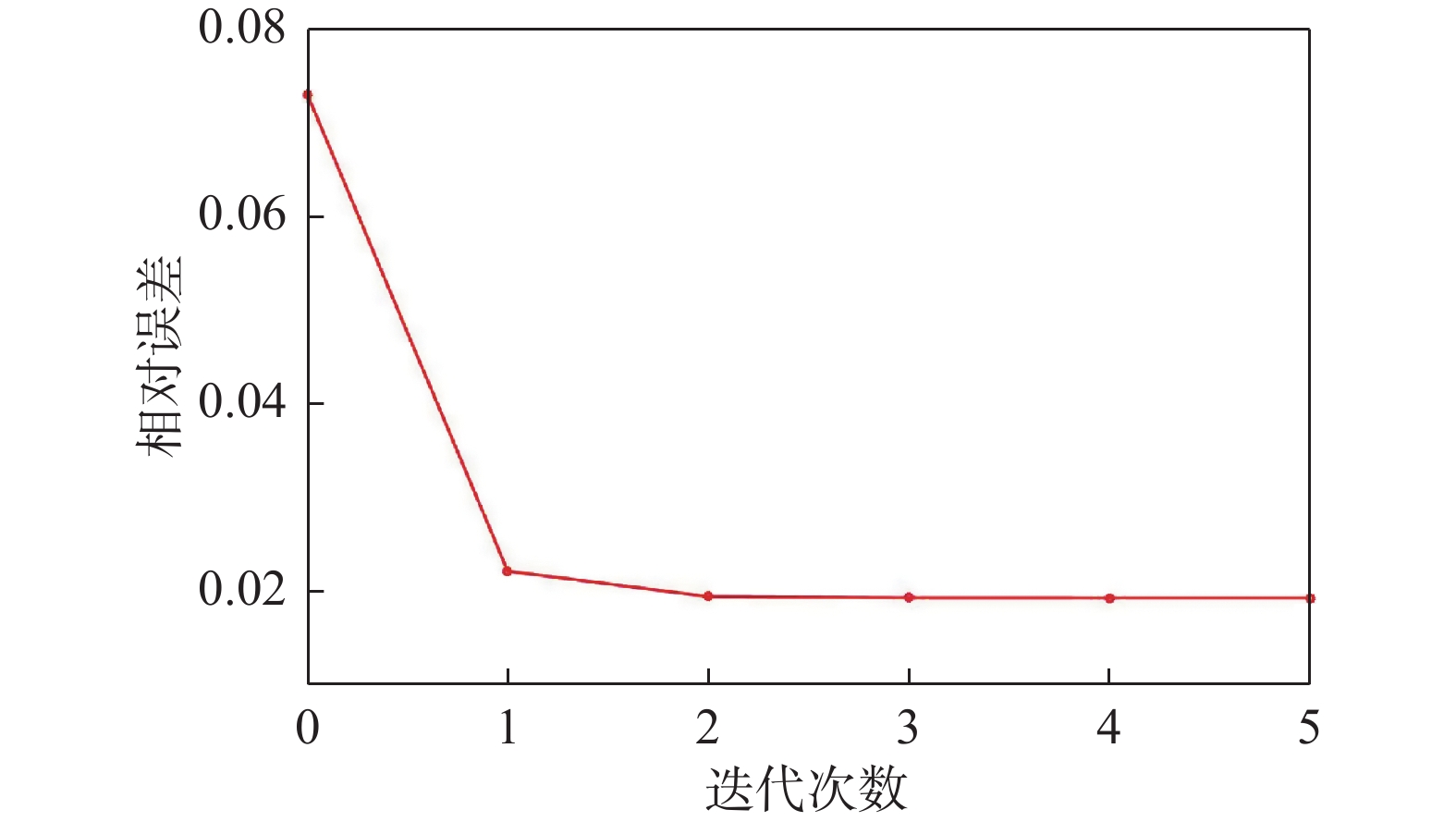
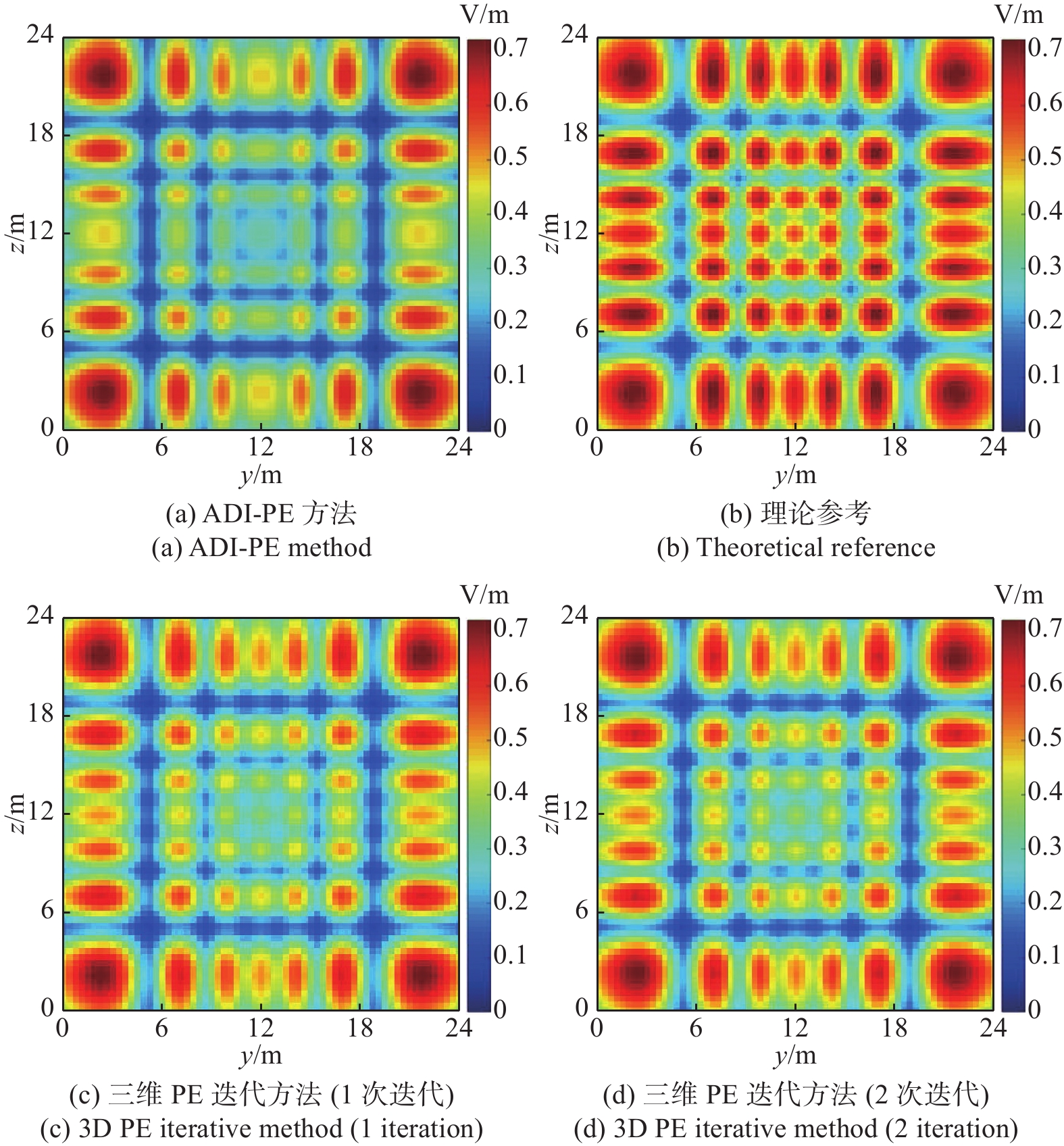
α=4 、N=5 、方位角φ=45° 时, 三种方法相对误差与仰角θ关系如图1所示. 可以看出,三种方法的相对误差都随着传播仰角的增大而增大,但三维PE迭代方法的相对误差比CN-PE方法和ADI-PE方法低,且能带来更高的计算精度.α=4 ,θ=3° 或6° ,φ=45° 时相对误差与参数N关系如图2所示. 可以看出,三种方法的相对误差随N的增大而减小,最后趋向相等的效果. 这是因为N与波长λ 及Δz 有关,在单位波长下,Δz 越大,N越小. 这说明较大的横截面网格步进会导致较大的误差,而所提的迭代方法相比CN-PE方法和ADI-PE方法能带来较低的误差效果. 此外,传播仰角角度越大,迭代方法降低误差效果越明显.α=4 ,N=5 ,θ=6° 时不同方位角对三种方法的影响如图3所示. 可以看出,三种方法在方位角90°和180°上达到相同的计算误差,但在45°和135°方位角上,本文推导的三维PE迭代方法能在对应的角度上降低计算误差.N=5 ,φ=45° ,θ=6° 时相对误差与α 关系如图4所示. 可以看出,三维PE迭代方法在α 较大时,能够减少相对误差. 这是因为α 与传播方向上的网格步进大小Δx 成正比关系,Δx 越大,CN-PE方法和ADI-PE方法计算出的误差越大;而三维PE迭代方法考虑了分裂项的补偿,分裂项与网格步进Δx 成正比关系.α=15 ,N=5 ,φ=45° 时本文提出的求解三维PE迭代方法的相对误差如图5所示. 可以看出:迭代次数为1时,误差降低效果明显;迭代次数为2时,迭代方法能够再次降低误差;当迭代一定次数时,所能降低误差的效果趋向于相等. 说明本文所提出的三维PE迭代方法在一定迭代次数下能降低计算误差.利用一个具体算例对本文所提方法性能进行验证. 将三维PE迭代方法、ADI-PE方法应用在一个密闭的隧道空间,隧道横截面规格为80
λ ×80λ . 工作频率为1 GHz、α=15 、N=5 、半功率波瓣宽度为15°的水平极化高斯源放置在隧道口正中间位置,离隧道口50 m处横截面的场强值仿真结果如图6所示. 用欧几里得误差范数计算相应的数值误差,分别为15.2%(ADI-PE方法)、13.6%(1次迭代)、12.8%(2次迭代),可以看出,所提的三维PE迭代方法计算场强值更接近参考值.此外,三维PE迭代方法与ADI-PE、CN-PE的计算效率对比如表1所示. 可以看出,虽然三维PE迭代方法比ADI-PE方法计算用时较多,但其时间增量在一定的线性增加范围,远低于CN-PE计算量. 即在少量的时间开销下,三维PE迭代方法能够提高PE求解的准确度.
表 1 三种方法计算效率对比Tab. 1 Comparison of computational efficiency方法 CN-PE方法 ADI-PE方法 三维PE迭代方法
(1次迭代)三维PE迭代法
(2次迭代)计算时间/s 585.628 1.728 3.151 4.028 3 结 论
本文提出一种求解三维PE的迭代方法. 对比现有的求解三维PE的ADI-PE和CN-PE方法,该方法能够提高计算精准度,且可通过迭代达到一定计算精度,是一种高效且计算精准度高的三维PE求解方法. 但该方法未考虑阻抗边界处理问题,是下一步研究的方向.
-
表 1 三种方法计算效率对比
Tab. 1 Comparison of computational efficiency
方法 CN-PE方法 ADI-PE方法 三维PE迭代方法
(1次迭代)三维PE迭代法
(2次迭代)计算时间/s 585.628 1.728 3.151 4.028 -
[1] LEVY, M F. Parabolic equation methods for electromagnetic wave propagation [M]. London: IEE Press, 2000.
[2] APAYDIN G, SEVGI L. Radio wave propagation and parabolic equation modeling [M]. Wiley-IEEE Press, 2017.
[3] 黎杨. 抛物型方程的有限差分解法及其在复杂电磁环境中的应用[D]. 武汉: 武汉理工大学, 2010. LI Y. The finite-difference method to parabolic equation and its application in complex electromagnetic environments [D]. Wuhan: Wuhan University of Technology, 2010. (in Chinese)
[4] 郭建炎, 王剑莹, 龙云亮. 森林中电波传播的抛物方程法[J]. 电波科学学报,2007,22(6):1042-1046. GUO J Y, WANG J Y, LONG Y L. Parabolic equation model for wave propagation in forest environments[J]. Chinese journal of radio science,2007,22(6):1042-1046. (in Chinese)
[5] GUO Q, ZHOU C, LONG Y L. Greene approximation wide-angle parabolic equation for radio propagation[J]. IEEE transactions on antennas and propagation,2017,65(11):6048-6056. doi: 10.1109/TAP.2017.2748222
[6] GUO Q, LONG Y L. Pade second-order parabolic equation modeling for propagation over irregular terrain[J]. IEEE antennas and wireless propagation letters,2017:2852-2855.
[7] 郭琪, 黎子豪, 朱琼琼, 等. 基于全局透射边界条件的宽角抛物方程电波预测模型[J]. 电波科学学报,2019,34(4):473-478. doi: 10.13443/j.cjors.2018110601 GUO Q, LI Z H, ZHU Q Q, et al. Radio propagation prediction model based on wide-angle parabolic equation with non-local boundary condition[J]. Chinese journal of radio science,2019,34(4):473-478. (in Chinese) doi: 10.13443/j.cjors.2018110601
[8] LYTAEV M S, VLADYKO A G. Split-step Padé approximations of the Helmholtz equation for radio coverage prediction over irregular terrain [C]// Advances in Wireless and Optical Communications (RTUWO), 2018.
[9] LYTAEV M S. Numerov-Padé scheme for the one-way Helmholtz equation in tropospheric radio-wave propagation[J]. IEEE antennas and wireless propagation letters,2020,19(12):2167-2171. doi: 10.1109/LAWP.2020.3026626
[10] ZHOU L, WANG D, MU Z, et al. LF Radio wave prediction at short ranges with high propagation angles over irregular terrain[J]. IEEE antennas and wireless propagation letters,2016,16:732-735.
[11] WANG D D, PU Y R, XI X L, et al. An analysis of narrow-angle and wide-angle shift-map parabolic equations[J]. IEEE transactions on antennas and propagation,2020,68(5):3911-3918. doi: 10.1109/TAP.2020.2963903
[12] MARTELLY R, JANASWAMY R. An ADI-PE approach for modeling radio transmission loss in tunnels[J]. IEEE transactions on antennas and propagation,2009,57(6):1759-1770. doi: 10.1109/TAP.2009.2019891
[13] HE Z, ZENG H, CHEN R S. Two way propagation modeling of expressway with vehicles by using the three-dimensional ADI-PE method[J]. IEEE transactions on antennas and propagation,2018,66(4):2156-2160. doi: 10.1109/TAP.2018.2805018
[14] HUANG L, WU X P, LI Z H, et al. A parallel FDTD/ADI-PE method for ultralarge-scale propagation modeling of ILS signal analysis[J]. IEEE antennas and wireless propagation letters,2020,19(12):2245-2249. doi: 10.1109/LAWP.2020.3029193
[15] WANG S, TEIXEIRA F L, JI C. An iterative ADI-FDTD with reduced splitting error[J]. IEEE microwave and wireless components letters,2005,15(2):92-94. doi: 10.1109/LMWC.2004.842835




































 下载:
下载: