0   引　言

多通道阵列雷达系统一般通过自适应目标探测技术实现在特定范围内进行监视搜索目标的功能，自适应目标探测的任务是在具有未知协方差矩阵的色噪声或杂波背景里判断出目标的有无^[1-8]。根据自适应处理的概念^[1]，要实现自适应处理须基于一个不含目标信息的训练数据组，这些训练数据被用来估计测试数据中的未知噪声协方差矩阵。众所周知，当训练数据量有限时，自适应检测效果不佳，检测性能急剧下降，研究指出当训练数据量小于系统维度的两倍时，雷达的检测概率会显著下降^[2]。

利用训练数据，研究人员提出了许多自适应检测器，如广义似然比检验(generalized likelihood ratio test, GLRT)^[3]、自适应匹配滤波器(adaptive matched filter, AMF)^[4]、自适应相关检测法^[5]和自适应子空间检测法(adaptive subspace detector, ASD)^[6]等，其均要求待检数据和训练数据相互独立且同分布，并具有相同或成缩放比例的噪声协方差。值得注意的是，为了确保估计噪声协方差矩阵的非奇异性，并获得出色的检测性能，这些检测器所需的训练数据量必须大于系统维度的两倍^[5]。实际雷达工作环境中，由于地形地貌海况的多样性、高大物体的遮蔽效应、孤立散射干扰的存在等原因^[7-11]，自适应目标检测可用的训练样本数据极度匮乏。因此，针对训练数据有限时的自适应检测问题，基于斜对称^[12-25]、知识辅助检测^[26]和对角加载法^[27]的方法得到了应用。其中，利用噪声协方差矩阵结构的先验知识可有效降低自适应处理对大量训练数据的要求。然而，上述检测方法^[3-6]没有利用雷达噪声协方差矩阵结构的先验知识，导致训练样本匮乏时上述检测方法的检测性能急剧衰减。

在实际雷达应用中，当雷达系统配置了对称间距的线性阵列或系统接收脉冲序列时域对称时^[12-24]，噪声协方差矩阵具有中心厄米特对称结构(也称作厄米特反对称)结构。中心厄米特对称结构指协方差矩阵具有双重对称性，即关于其主对角线厄米特对称且同时关于其主对角线反对称。协方差中心厄米特对称的一个特例即为托普利兹结构。为简洁起见，下文中的 “双对称”结构一律指“中心厄米特对称”结构。双对称结构在许多方法中得到使用，例如雷达空时处理^[12]、匹配滤波箱频谱估计^[13]、波达角估计^[14]、多频带广义似然比检测^[15]等，均证实其有效缓解了自适应训练样本的负担量。

自适应目标检测通常基于精确的目标信息设计假设检验模型，现有文献证明^[28-31]，目标角度信息获取(一般在方向余弦域^[28-29]中执行)通常在雷达目标检测事件触发后启动。首先，通过自适应检测器对主波束目标进行检测。然后，如果在天线主波束范围内发现目标，就需要采用特定信号处理技术，如角度估计，即通过最大似然法^[30]、单脉冲算法^[30]、广义单脉冲算法^[28]、广义自适应多维单脉冲算法^[31]来获取天线波束内的目标信息。此外，还可以考虑目标检测和目标信息获取的联合处理方法^[32-33]，即在进行目标检测的同时，通过单脉冲空域处理直接提供目标信息，这可用于多功能相控阵雷达的每个搜索波束上及目标确认过程，探测器触发首次探测后，需要确认目标是否存在，若存在就同时输出估计的目标信息。需要指出的是，本文也考虑了目标检测和目标角度信息获取的联合处理方法。然而，与传统联合处理方法^[32-33]对样本量要求较严苛不同，考虑到实际雷达工作环境中多因素导致的训练样本量匮乏，本文采取了协方差矩阵辅助的目标检测方法，可减轻阵列雷达对大量训练数据的需求。

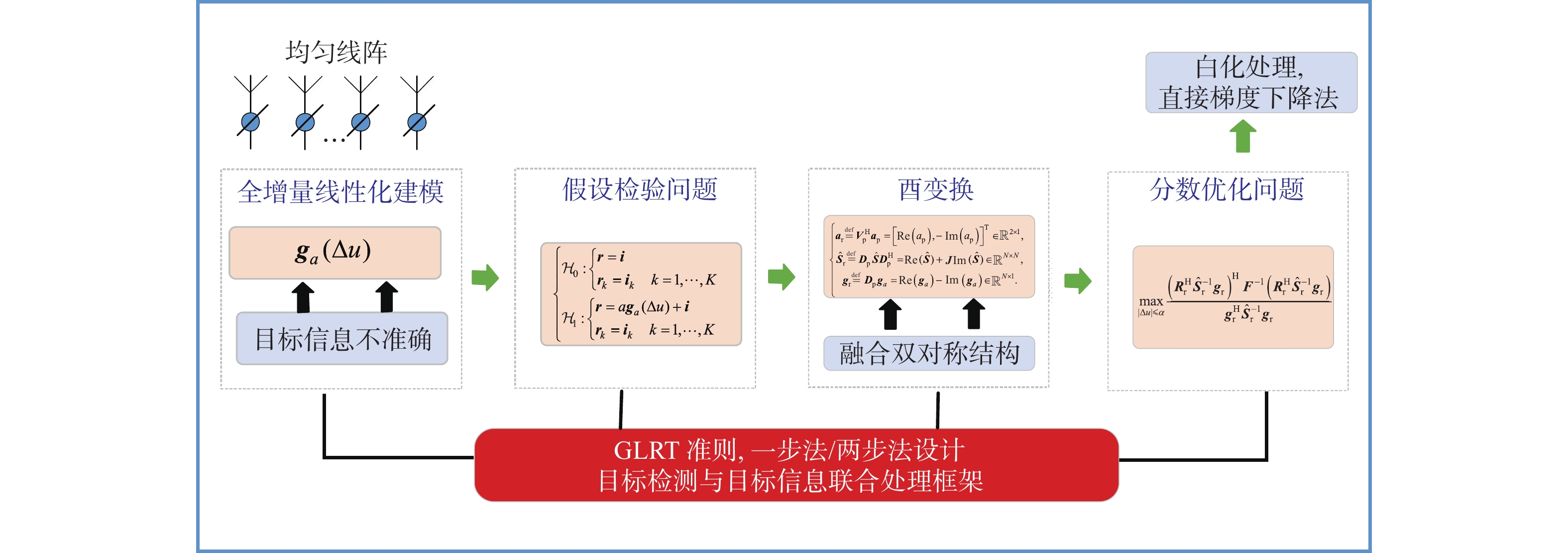
综上所述，本文提出了协方差结构辅助的全增量线性化模型自适应目标检测方法，该方法采取联合处理思想，充分利用噪声协方差的双对称结构信息，在目标信息不准确情况下，将阵列导向矢量建模为全增量线性化模型，然后利用酉矩阵变换设计协方差结构辅助的检测，通过将该检测问题转化为分数优化问题并白化处理推导出最终检测统计量，从而实现对目标的有效检测。利用仿真实验对所提方法性能进行验证，并将结果与现有检测方法进行了对比，验证了本文方法的有效性，可有效改善目标在复杂敏感环境下的检测性能。

1   问题描述

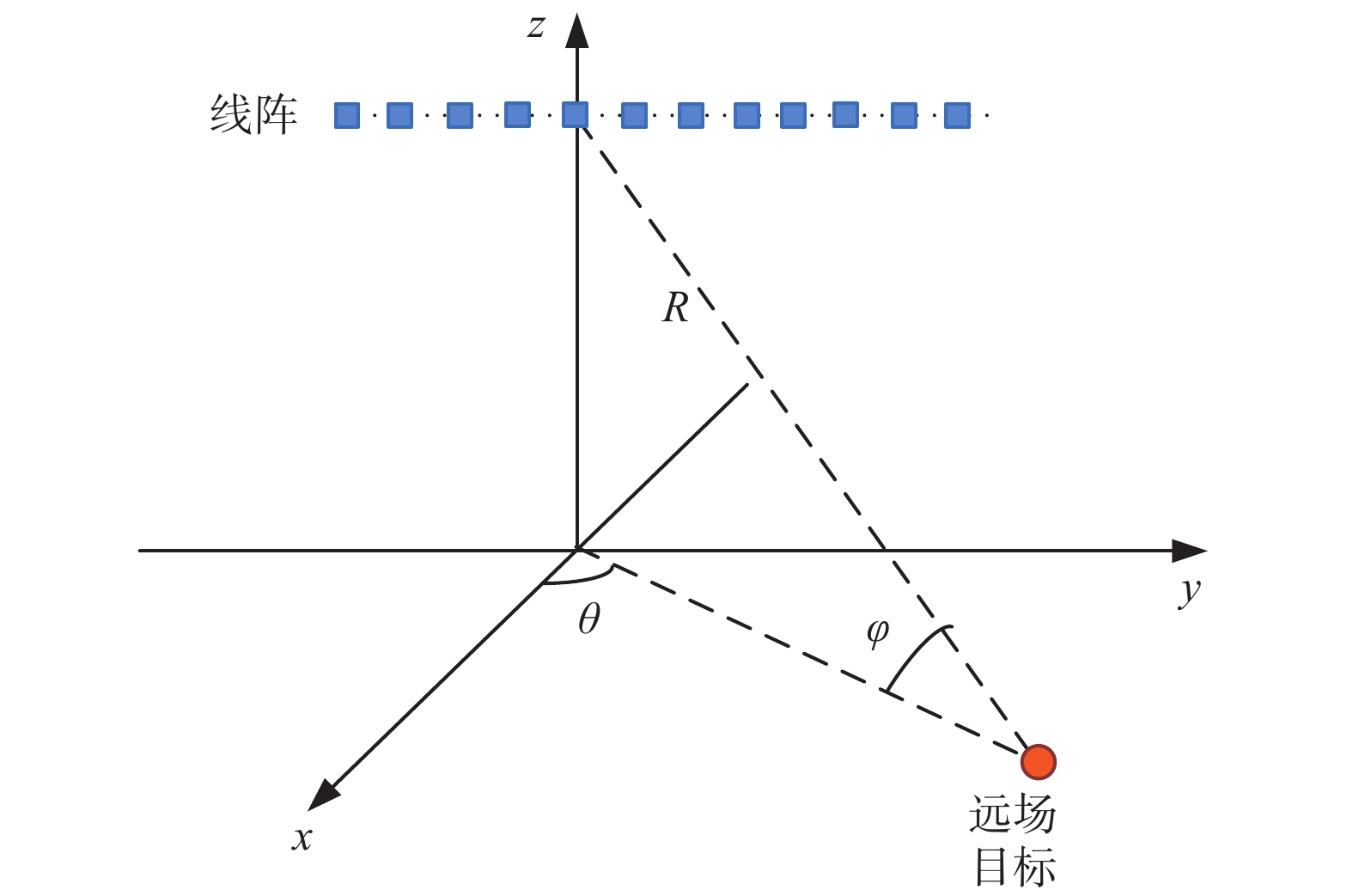
多通道阵列雷达系统及场景中的目标如图1所示。考虑由N个阵元组成的一维均匀天线阵列，雷达接收系统在空间接收回波数据，假定一个远场目标位于距离R、方位角$\theta$、俯仰角$\varphi$处，则目标回波信号可被建模为

式中：$a$是未知信号幅度；$u = \sin (\theta )\cos (\varphi )$是目标在空间余弦坐标系下的方位位置；${\boldsymbol{g}}(u)$是目标信号导向矢量。对于一维线性阵列，目标信号导向矢量可表示为

式中：${\lambda _0}$是雷达工作波长；${x_i}$是阵元位置；${\mathbb{C}^{m \times n}}$是维数为$m \times n$的复矩阵空间。

图  1  多通道阵列雷达几何位置示意图

Fig.  1  Multi-channel array radar geometry location

下载: 全尺寸图片 幻灯片

${\boldsymbol{g}}(u)$表示阵列转向方向与目标到达方向一致情况下的目标真实导向矢量，实际场景中阵列转向往往与目标角度信息有一定的偏差。为了描述它们之间的不匹配现象，本文将目标导向矢量进一步描述为全增量线性化模型，利用雷达波束发射方向$\hat u = \sin (\hat \theta )\cos (\hat \varphi )$周围阵列流形的线性化，其中目标空间方位余弦偏差$\Delta u = \sin (\theta )\cos (\varphi ) - \sin (\hat \theta )\cos (\hat \varphi )$，则导向矢量可被近似表达如下：

式中：估计导向矢量${\boldsymbol{g}} = {\boldsymbol{g}}(\hat u)$；偏导${\dot {\boldsymbol{g}}_u} = {\left. {\dfrac{{\partial {\boldsymbol{g}}(u)}}{{\partial u}}} \right|_{u = \hat u}}$。

假设有用的目标回波信号即待测数据淹没在复高斯噪声中，此外共有$K \geqslant N$个训练数据(保证协方差矩阵以概率1非奇异)，每个训练数据都不包含任何目标信号分量，并且具有与待测数据噪声相同的协方差结构。根据雷达波束指向方向的全增量线性化表达式(3)，探测问题可建模为一个复合二元假设

式中：${\boldsymbol{r}}$是主数据；${{\boldsymbol{r}}_k}$是训练数据；${\boldsymbol{i}}$和${{\boldsymbol{i}}_k}$是复值零均值协方差矩阵为${\boldsymbol{S}}$的高斯噪声；导向矢量${{\boldsymbol{g}}_a}(\Delta u)$中未知的方位余弦偏移量$|\Delta u| \leqslant \alpha$，$\alpha$是约束全增量线性化导向矢量与目标真实导向矢量一致性的超参数，合理的选择是目标3 dB波束宽度^[30]。噪声分量${{\boldsymbol{r}}_k}$和${\boldsymbol{r}}$为独立的复高斯循环随机矢量，其协方差矩阵未知，本质可表示为

双对称结构可有效降低一维阵列雷达对训练数据量的要求，当对称间隔的一维线性阵列以原点为相位中心时或接收的脉冲序列对称分布时，未知协方差矩阵${\boldsymbol{S}}$和导向矢量${{\boldsymbol{g}}_a} = {{\boldsymbol{g}}_a}(\Delta u)$具有双对称结构，即${\boldsymbol{S}} = {\boldsymbol{J}}{{\boldsymbol{S}}^{\boldsymbol{*}}}{\boldsymbol{J}}$，${{\boldsymbol{g}}_a} = {\boldsymbol{J}}{{\boldsymbol{g}}_a^*}$，其中反对称矩阵${\boldsymbol{J}} \in {\mathbb{R}^{N \times N}}$可表示为

值得注意的是，方向余弦偏移量$\Delta u$、未知信号幅度$a$和协方差矩阵${\boldsymbol{S}}$在式(4)中是未知的，本文采用最大似然准则进行未知参数优化求解。基于以上信号模型，本文提出了一种协方差结构辅助的全增量线性化模型自适应目标检测方法，该方法采取联合处理思想，充分利用噪声协方差的双对称结构的信息，在目标信息不准确情况下，设计基于GLRT的检测器。

2   协方差结构辅助的全增量线性化模型检测方法

本节中，将详细描述所提出的协方差结构辅助的全增量线性化模型自适应目标检测方法，在目标检测和目标信息获取联合处理的框架下，考虑一步法和两步法两种检测器设计思路。对于一步法而言，其考虑所有数据，用每个假设检验下的最大似然估计值替换未知参数；对于两步法而言，首先假设噪声协方差矩阵已知，基于GLRT准则推导出检测统计量，再用估计的协方差矩阵代替检测统计量中的假定已知的协方差矩阵。

2.1   一步法检测器

定义训练数据集${{\boldsymbol{R}}_{\text{s}}} = \left[ {{{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}, \cdots ,{{\boldsymbol{r}}_K}} \right] \in {\mathbb{C}^{N \times K}}$和待测数据${{\boldsymbol{R}}_{\text{p}}} = {\boldsymbol{r}} \in {\mathbb{C}^{N \times 1}}$，则一维线性阵列雷达${\boldsymbol{R}}$和${{\boldsymbol{R}}_{\text{s}}}$的联合概率密度函数可表示为：

式(8)中双对称结构的${\boldsymbol{\hat S}}$、待测数据${{\boldsymbol{R}}_{\text{p}}}$和信号幅度${{\boldsymbol{a}}_{\text{p}}}$表达式如下：

接下来，需要将式(7)中的变量从复数值域转换为实数值域，以便进一步求解出检测问题的闭式检测统计量。首先，定义以下两个酉矩阵：

${{\boldsymbol{D}}_{\text{p}}}$可以将复数转换为只包含实部和虚部的两个数值，${{\boldsymbol{V}}_{\text{p}}}$可以将实数值和虚数值都转换为实数值^[15]。因此，根据以上酉矩阵，${{\boldsymbol{R}}_{\text{p}}}$可以转换为以下形式：

式中：${{\boldsymbol{R}}_{{\text{er1}}}} = {{\boldsymbol{D}}_{\text{p}}}{{\boldsymbol{R}}_{\text{e}}}$；${{\boldsymbol{R}}_{{\text{or1}}}} = - {\text{j}}{{\boldsymbol{D}}_{\text{p}}}{{\boldsymbol{R}}_{\text{o}}} \in {\mathbb{R}^{N \times 2}}$；${\mathbb{R}^{m \times n}}$是维数为$m \times n$的实矩阵空间。

进一步，可将${\boldsymbol{\hat S}}$、${{\boldsymbol{g}}_a}$和${{\boldsymbol{a}}_{\text{p}}}$转换为

将式(16)和(17)代入联合概率密度函数(7)中可得

式中：

根据式(18)，基于GLRT检验准则，可将基于一步法的协方差结构辅助的全增量线性化模型检测决策式表示如下：

式中，$\xi$是为了确保恒虚警率${P_{{\text{fa}}}}$的检测阈值。

为求解式(21)，分别将式(21)中分子和分母关于协方差矩阵${{\boldsymbol{S}}_{\text{r}}}$最大化，对检测式进一步简化可得

之后将式(22)分母关于${{\boldsymbol{a}}_{\text{r}}}$求最小化可得

将式(23)代入到检测式(22)可得

为方便起见，将式(24)简写为

式中：${{\boldsymbol{\psi }}_1} = {\boldsymbol{I}} + {\boldsymbol{R}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{ - 1}{{\boldsymbol{R}}_{\text{r}}}$；${\boldsymbol{\psi }} = {{\boldsymbol{\psi }}_1} - \dfrac{{{\boldsymbol{x}}{{\boldsymbol{x}}^{\text{T}}}}}{{{\boldsymbol{g}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{{{ - 1}}}{{\boldsymbol{g}}_{\text{r}}}}}$，${\boldsymbol{x}} = {\boldsymbol{R}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{ - 1}{{\boldsymbol{g}}_{\text{r}}}$。

由于只有分母包含待优化量，因此将仅包含方位余弦偏移$\Delta u$的分母转化为如下优化问题：

利用行列式的性质^[20]，式(26)可以进一步简化为

最后，得到以下分数优化问题：

式中，${\boldsymbol{F}} = {\boldsymbol{I}} + {\boldsymbol{R}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{ - 1}{{\boldsymbol{R}}_{\text{r}}}$。

定义以下白化量：

式中，${{\boldsymbol{\tilde R}}_{\text{r}}} = {{\boldsymbol{R}}_{\text{r}}}{{\boldsymbol{F}}^{ - 1/2}}$。通过白化量，将式(28)转化为

现在，对于优化问题(30)求其闭式最优解$\Delta {u_{{\text{PD}}}}$。由于式(30)是一个连续函数，且方向余弦偏差$\Delta u$位于闭集合$[ - \alpha ,\alpha ]$，则其候选最优解是边界点以及满足一阶最优条件的可行点，即目标函数导数等于零。因此，式(30)的最优解$\Delta {u_{{\text{PD}}}}$是

式中，$\eta$是对式(31)中目标函数求导后，使其导数为零(绝对值小于$\alpha$)的实根。对目标函数求导可将其化为

二次项系数$p$、一次项系数$q$以及常数项$c$分别为：

式中，$|| \cdot ||$是求欧几里得二范数。

从而，根据直接梯度下降法，可由式(32)中的方程直接求解得出式(31)的最优解$\Delta {u_{{\text{PD}}}}$。将该最优解进一步代入式(22)可得基于一步法的反对称协方差结构辅助的全增量线性化(persymmetric covariance structure-aided fully incremental linearized one-step method, PCSFIL-OM)模型检测器的最终检测统计量如下：

式中：${{\boldsymbol{\tilde g}}_{\text{r}}} = {{\boldsymbol{D}}_{\text{p}}}{\boldsymbol{J}}{({\boldsymbol{g}} + {{\boldsymbol{\dot g}}_u}\Delta {u_{{\text{PD}}}})^*}$；${{\boldsymbol{\tilde a}}_{\text{r}}} = \dfrac{{{\boldsymbol{R}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{{{ - 1}}}{{{\boldsymbol{\tilde g}}}_{\text{r}}}}}{{{\boldsymbol{\tilde g}}_{\text{r}}^{\text{T}}{\boldsymbol{\hat S}}_{\text{r}}^{{{ - 1}}}{{{\boldsymbol{\tilde g}}}_{\text{r}}}}}$。

2.2   两步法检测器

两步GLRT检测器中，首先假设目标协方差矩阵${\boldsymbol{S}}$是已知的，则基于两步法的GLRT 检测决策式为

其中概率密度函数分别为：

与式(24)推导类似，式(37)可以写成

式中：${{\boldsymbol{\dot R}}_{\text{r}}} = {{\boldsymbol{S}}_{\text{r}}^{ - \frac{1}{2}}}{{\boldsymbol{R}}_{\text{r}}}$；${\boldsymbol{\dot G}} = {{\boldsymbol{\bar g}}_{\text{r}}}{({{\boldsymbol{\bar g}}_{\text{r}}}^{\text{T}}{{\boldsymbol{\bar g}}_{\text{r}}})^{ - 1}}{{\boldsymbol{\bar g}}_{\text{r}}}^{\text{T}}$，${{\boldsymbol{\bar g}}_{\text{r}}} = {{\boldsymbol{S}}_{\text{r}}^{ - \frac{1}{2}}}{{\boldsymbol{g}}_{\text{r}}}$。

从而，可将式(40)进一步简化为

类似地，可以通过直接梯度下降法获得式 (41)的全局最优值，记为$\Delta {u_{{\text{PD-2S}}}}$。然后，计算协方差矩阵${\boldsymbol{S}}$的估计值为

将式(42)代入式(41)中解出的检测统计量，替换原来假定已知的协方差矩阵，得到基于两步法的反对称协方差结构辅助的全增量线性化 (persymmetric covariance structure-aided fully incremental linearized two-step method, PCSFIL-TM)模型检测器的最终检测统计量如下：

式中：${\boldsymbol{\dot{ \tilde G}}} = {{\boldsymbol{\tilde g}}_{\text{r}}}{({{\boldsymbol{\tilde g}}_{\text{r}}}^{\text{T}}{{\boldsymbol{\tilde g}}_{\text{r}}})^{ - 1}}{{\boldsymbol{\tilde g}}_{\text{r}}}^{\text{T}}$，${{\boldsymbol{\tilde g}}_{\text{r}}} = {{\boldsymbol{S}}_{\text{r}}^{ - \frac{1}{2}}}{{\boldsymbol{\tilde g}}_{{\text{r2}}}}$，${{\boldsymbol{\tilde g}}_{{\text{r2}}}} = {{\boldsymbol{D}}_{\text{p}}}{\boldsymbol{J}}({\boldsymbol{g}} + {{\boldsymbol{\dot g}}_u}\Delta {u_{{\text{PD-2S}}}})^*$。

综上所述，本文所提协方差结构辅助的全增量线性化模型检测方法的主要框架如图2所示。

图  2  协方差结构辅助的全增量线性化模型检测主要框架思路图

Fig.  2  Covariance structure-assisted full incremental linearization model detection main framework idea map

下载: 全尺寸图片 幻灯片

3   仿真实验

在本节中，将验证本文提出的协方差结构辅助的全增量线性化模型自适应目标检测方法，其中均匀环境中的协方差矩阵被建模为${\boldsymbol{M}} = {{\boldsymbol{M}}_{\text{J}}} + \sigma _{\text{a}}^{\text{2}}{\boldsymbol{I}}$，${{\boldsymbol{M}}_{\text{J}}}$为干扰协方差矩阵，$\sigma _{\text{a}}^{\text{2}}$为白噪声功率电平(本文假设为0 dB)。假设干扰机数量为${J_{{\text{num}}}}$，则干扰协方差矩阵可表示为

式中：$P_i^2$是第i个干扰的干扰功率；${{\boldsymbol{g}}_{\text{J}}}({u_i})$是干扰导向矢量。

本节中，考虑两个干扰位于${u_1} = 0.1$和${u_2} = 0.3$，它们的干噪比分别为${\text{JN}}{{\text{R}}_{\text{1}}}{\text{ = 30 dB}}$和${\text{JN}}{{\text{R}}_{\text{2}}}{\text{ = 40 dB}}$，将白噪声功率电平$\sigma _{\text{a}}^{\text{2}}$转换为线性功率(单位W)，即$\sigma _{{\text{a\_linear}}}^2 = {10^{\frac{{\sigma _{\mathrm{a}}^2}}{{10}}}}$，同理将第$i$个干扰机的干噪比转换为${\text{JN}}{{\text{R}}_{i\_{\text{linear}}}} = {10^{\frac{{{\text{JN}}{{\text{R}}_i}}}{{10}}}},i = 0,1$，则第$i$个干扰的干扰功率为$P_i^2 = {\text{JN}}{{\text{R}}_{i{\text{\_linear}}}}\sigma _{{\text{a\_linear}}}^2$。

为评估本文所提方法的检测性能，通过采取蒙特卡洛实验来估计检测概率$({P_{\text{d}}})$，考虑到计算量的限制，本文虚警概率设置为${10^{ - 3}}$^[2]，检测概率和检测门限均通过${10^5}$次蒙特卡洛实验得到。信干噪比${\text{SINR}} = |a{|^2}{{\boldsymbol{g}}^{\text{H}}}{\boldsymbol{M}}_{\text{J}}^{ - 1}{\boldsymbol{g}}$。此外，为验证本文提出的检测器的检测性能，将所提联合检测器与传统的GLRT检测方法^[3]、AMF检测方法^[4]、子空间(subspace detect, SD)检测方法^[6]、SD-AMF检测方法^[34]、广义似然比线性阵列流形(generalized likelihood ratio test linear array manifolds，GLRT-LAM)检测方法和GLRT-LAM-AMF检测方法^[32]进行了对比，上述对比检测器的统计检测式如下：

式中：${\boldsymbol{S}} = \dfrac{1}{K}\displaystyle \sum\limits_{k = 1}^K {{{\boldsymbol{r}}_k}} {\boldsymbol{r}}_k^{\text{H}}$是噪声估计协方差矩阵；${{\boldsymbol{G}}_{{\text{SD}}}} = [{\boldsymbol{g}},\Delta u]$；$\hat \Delta {\boldsymbol{\theta }}_{{\text{LAM}}}^ \star$是估算的目标角度信息。

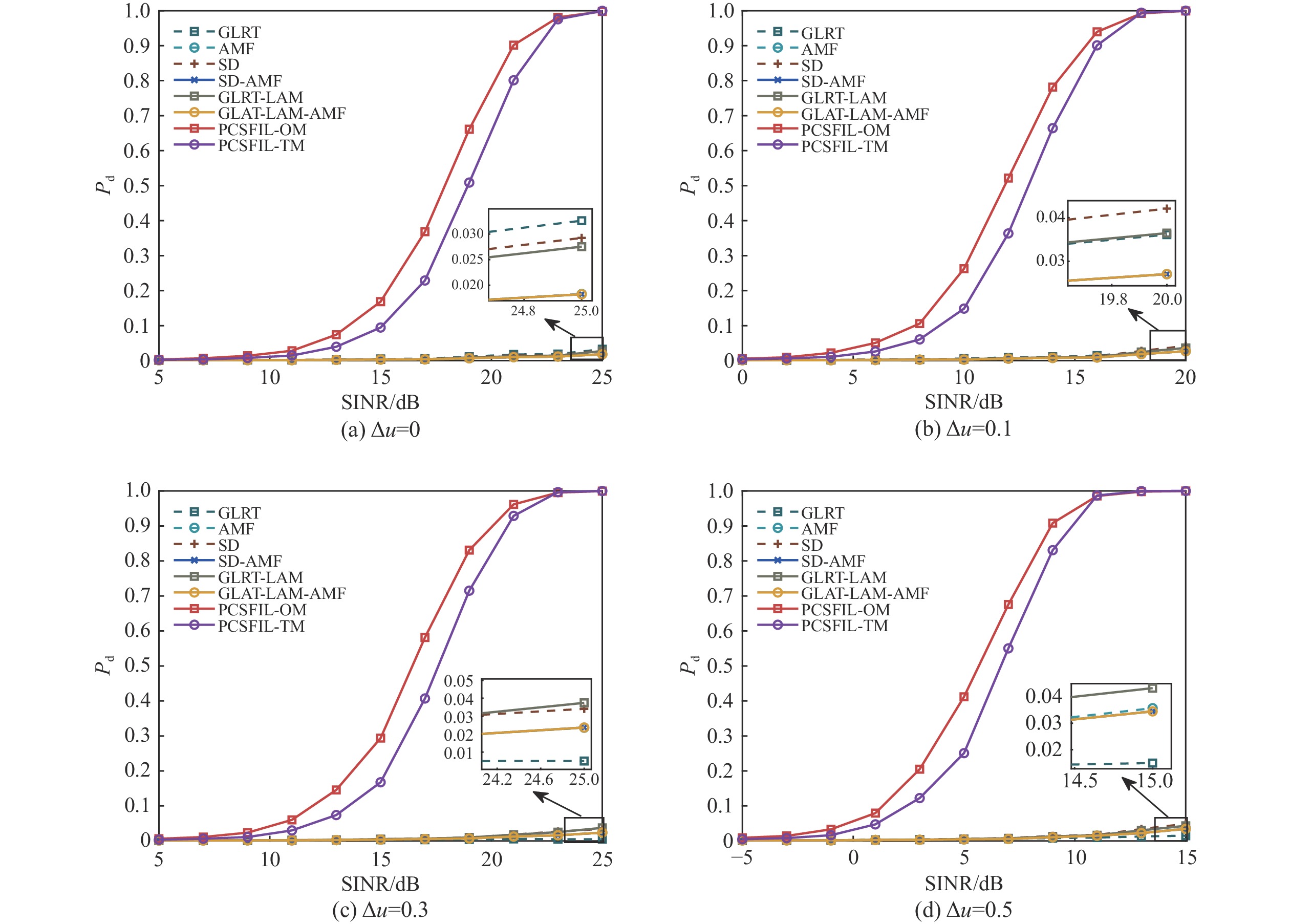
在仿真实验数据中，设置一维阵列的阵元数$N = 8$，一维阵列均匀分布，距离间隔为${d_{\text{x}}} = {\lambda _0}/2$，其中${\lambda _0}$是雷达发射电磁波波长。假设阵列坐标中心位于一维阵列的中心，则阵列分布为

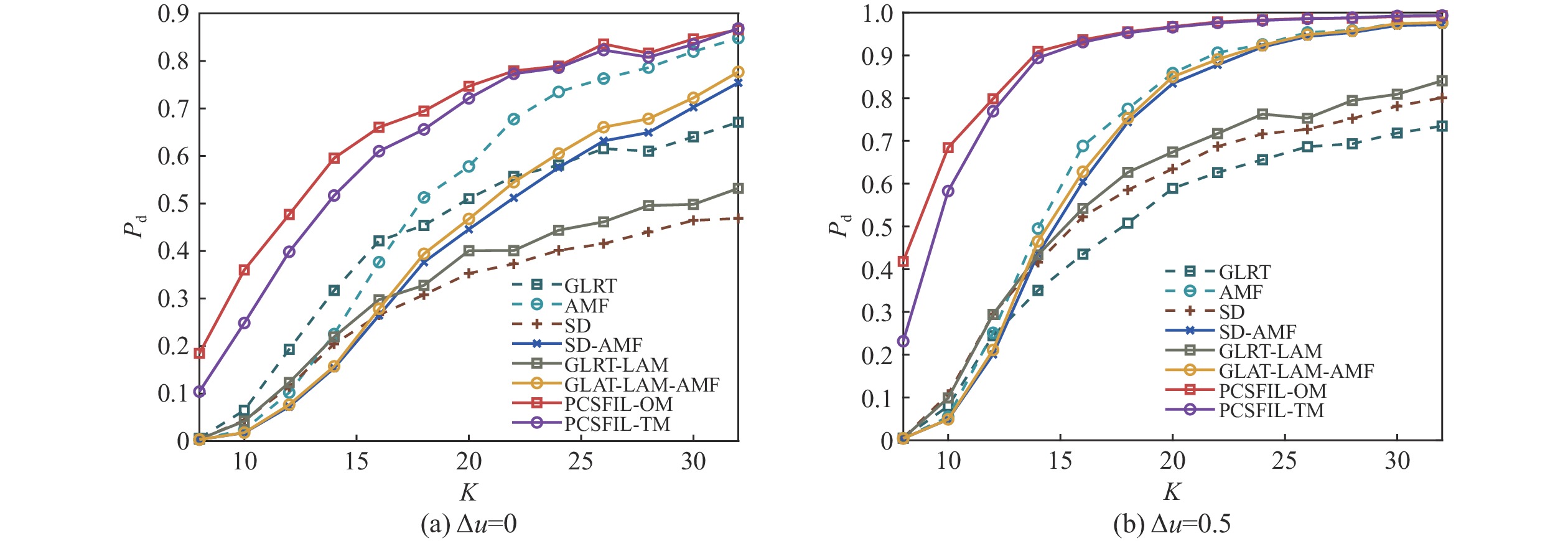
图3是训练样本数充足(K=2N=16)的情况下，在一维均匀线阵中不同失配情况下各检测器的检测概率曲线，其中超参数$\alpha = 0.5$，目标余弦位移偏移量$\Delta u = 0$、$\Delta u = 0.1$、$\Delta u = 0.3$和$\Delta u = 0.5$代表不同的导向矢量失配情况。从图3(a)可以看出：当${\text{SINR}} > 10\;{\text{dB}}$时，本文所提检测器PCSFIL-OM和PCSFIL-TM的检测概率均高于其他现有检测器，在${\text{SINR}} = {\text{15 dB}}$左右时，本文所提检测器的检测概率值与其他对比检测器中检测概率值最大相差0.4左右；无失配检测器AMF、联合检测器GLRT-LAM-AMF检测性能曲线与GLRT和SD-AMF相近，检测器SD和GLRT-LAM的检测性能上升趋势最慢。从图3(b)～(d)可以看出：当目标导向矢量处于不同的失配情况时，本文所提检测器的检测性能仍然保持最优，其次是GLRT-LAM和GLRT-LAM-AMF；当$\Delta u = 0.3$及$\Delta u = 0.5$时，检测器GLRT的检测性能下降，低于其他现有的检测器。综合图3仿真${P_{\text{d}}}$曲线可得，在训练数据充足情况下，本文所提方法在不同失配情况下检测性能均高于其他对比检测器，揭示了所提方法通过估计目标到达余弦位移偏移量，可在不同失配情况下有效提高检测性能。

图4是训练样本数不充足(K=N=8)的情况下，在一维均匀线阵中不同失配情况下各检测器的检测概率曲线。图4(a)显示，当训练数据量降低为原来的一半时，本文所提检测器PCSFIL-OM和PCSFIL-TM的检测性能仍然保持最优，而其他所有对比检测器的检测性能均大幅下降，在高${\text{SINR}}$条件下仍然最低。图4 (b)～(d)显示，在不同的导向矢量失配情况下，本文所提检测器的检测性能受影响不大，检测性能衰减较低，且远高于其他对比检测器。综合图4仿真${P_{\text{d}}}$曲线可得，本文所提检测器在小样本训练支持下，其检测概率高于现有检测器，揭示了所提双对称联合检测器对训练样本减少以及失配情况具有更强的稳健性。

图  3  训练数据充足情况下各检测器在不同失配情况下的检测曲线

Fig.  3  Detection curves of each detector for different mismatches with sufficient training data

下载: 全尺寸图片 幻灯片

图  4  训练数据不充足情况下各检测器在不同失配情况下的检测曲线

Fig.  4  Detection curves of each detector for different mismatches with insufficient training data

下载: 全尺寸图片 幻灯片

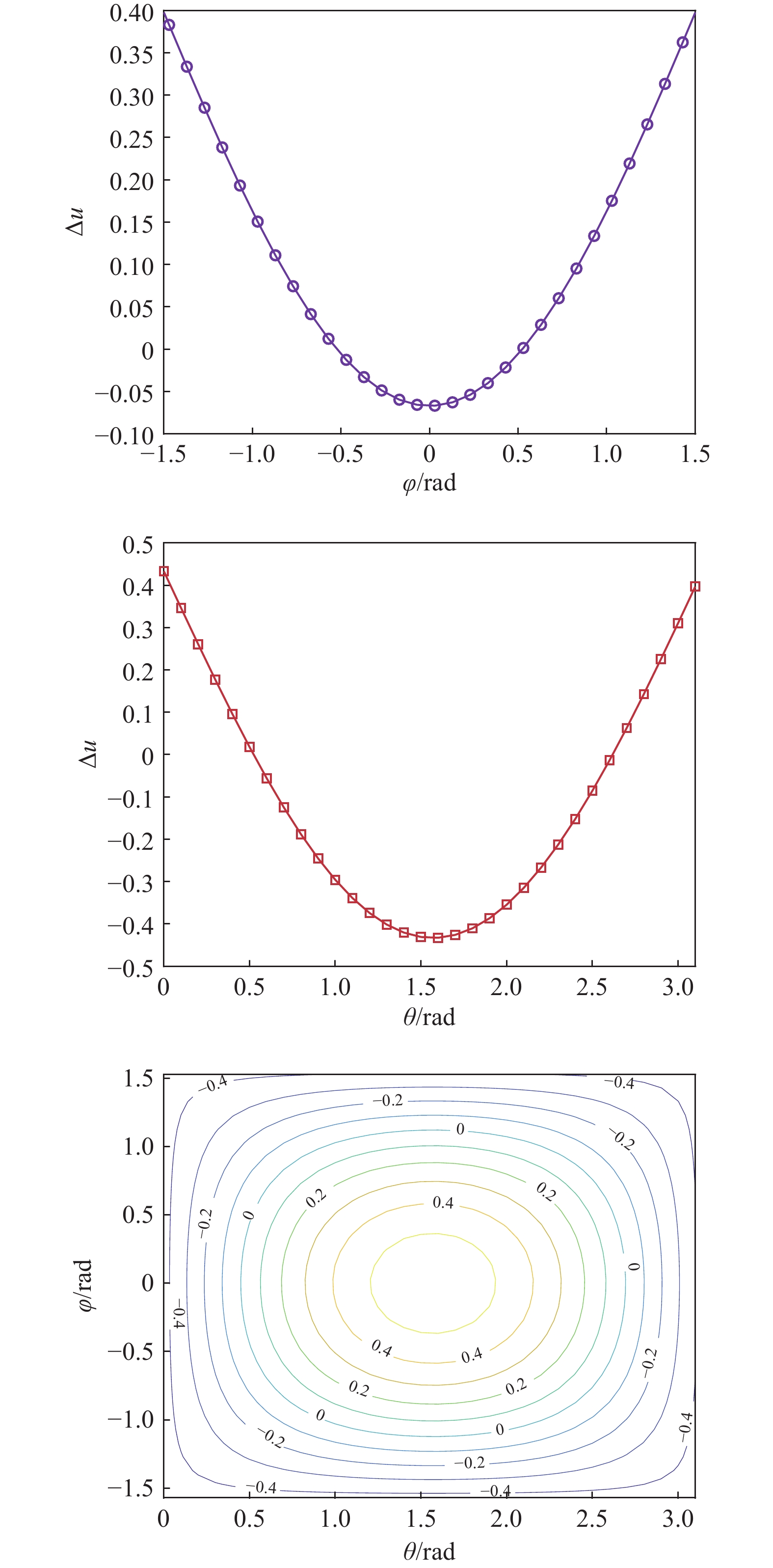
图5显示了方位角$\theta$和俯仰角$\varphi$变化时方位余弦偏差$\Delta u$的变化情况，假设目标位于$\theta = \varphi = {30{\text{°}}}$(弧度${30{\text{°}}} \cdot \dfrac{{\text{π }}}{{180}}{\text{rad}}$)处。从图5(a)与图5(b)可以看出，$\theta$和$\varphi$与$\Delta u$并非单调关系。从图5(c)可以看出，当$\Delta u$相同时可能经历了不同的方位角和俯仰角变化，$\Delta u$失配情况的变化由方位角和俯仰角共同决定，而不随着其中任意一个角度的变化而单调递增或单调递减。综合图5可得，对所有检测器而言，当$\Delta u$增加时，实现相同检测概率与$\Delta u$并非单调关系。

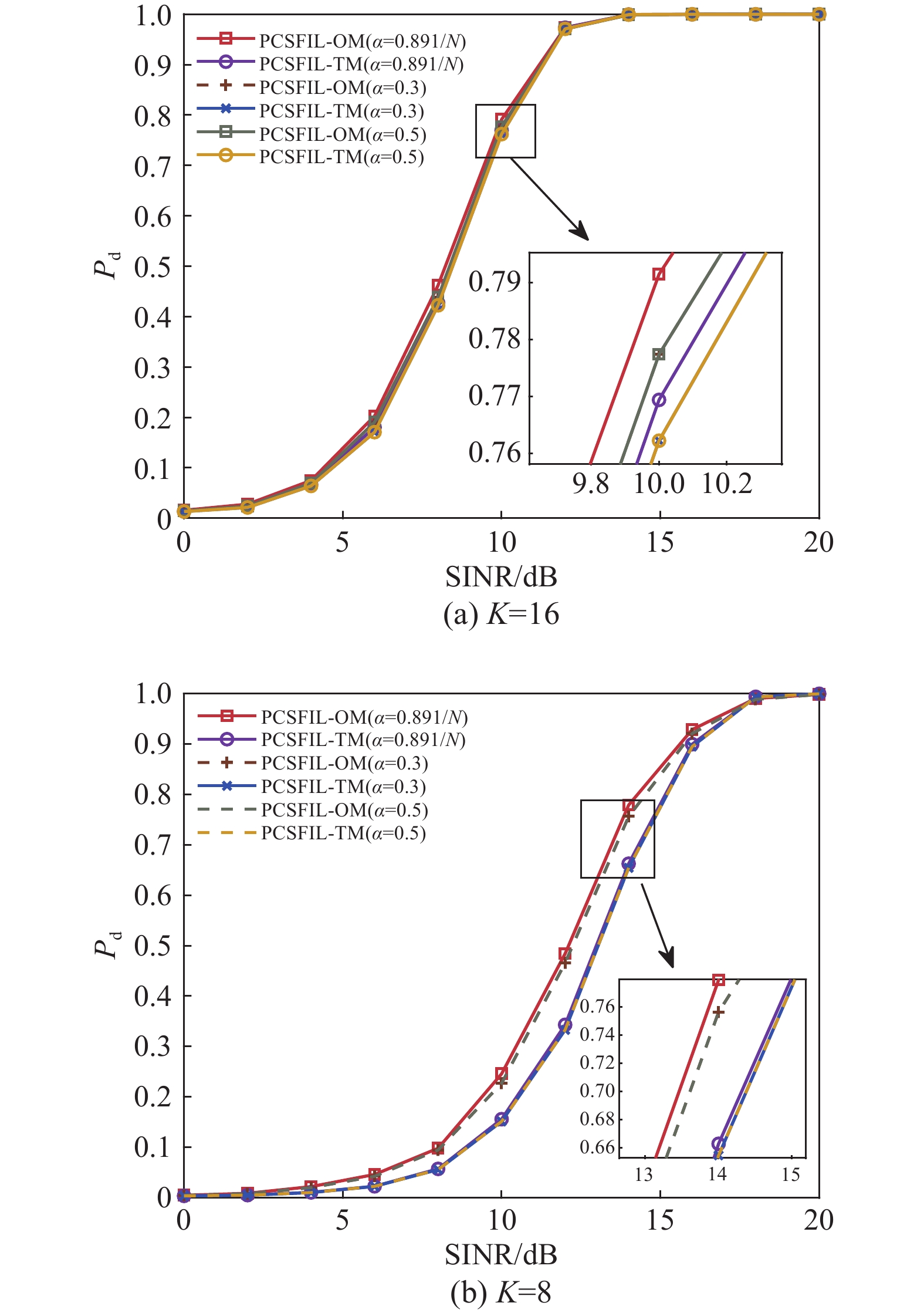
图6(a)与图6(b)分别是训练数据为K=2N和K=N时本文所提检测器在不同$\alpha$下的检测概率曲线，其中$\Delta u = 0.1$。从图6(a)可以看出，$\alpha$为3 dB波束宽度(即α=0.891/N)相比于其他约束水平其检测性能提升了0.01左右，且检测性能基本保持相同。从图6(b)可以看出，在训练数据量不充足条件下， PCSFIL-OM比PCSFIL-TM的检测性能高0.1左右，但同一检测器在不同的约束水平$\alpha$下其检测概率曲线也基本相同。综合图6可得，$\Delta u$通过直接下降梯度法进行优化，当取同一个$\Delta u$时，在不同超参数$\alpha$下本文所提检测器的检测性能变化不显著。

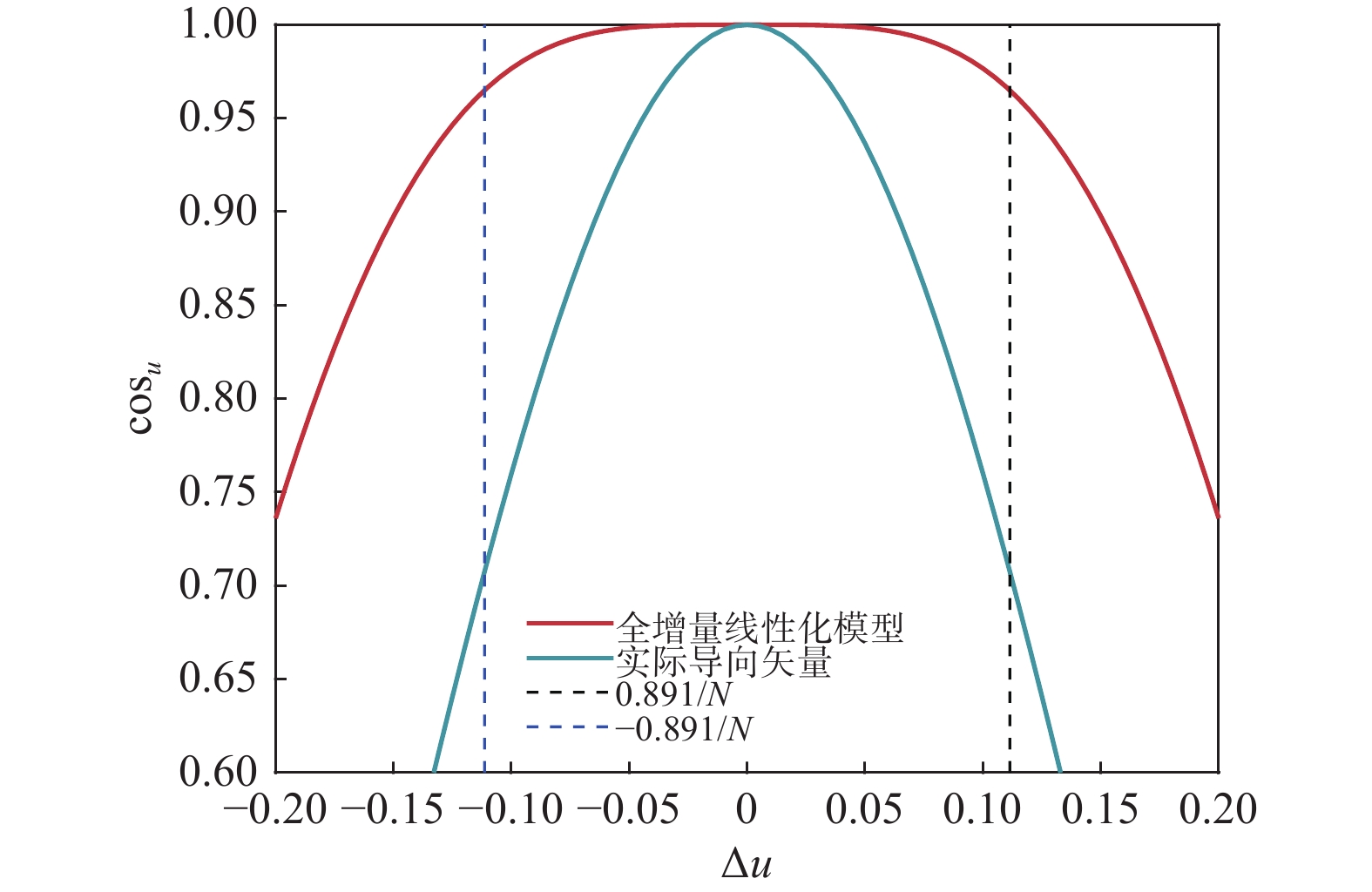
此外，由于一维阵列雷达探测方位与目标真实方位不一致，导致目标真实导向矢量与实际导向矢量之间的失配。本文所提方法通过估计目标到达方向余弦偏差，构建全增量线性化模型减弱导向矢量失配引起的检测性能衰减。为评估双对称全增量线性化模型近似的准确性，定义真实导向矢量与近似导向矢量之间归一化相关性(不匹配角度余弦)的大小为

图  5  方位角θ和俯仰角φ与余弦偏差∆u的变化关系

Fig.  5  Variation of azimuth θ and pitch φ with cosine deviation ∆u

下载: 全尺寸图片 幻灯片

图  6  不同训练数据K下本文检测器的检测曲线

Fig.  6  Detection curves of the proposed detector with different training data K

下载: 全尺寸图片 幻灯片

式中：${\boldsymbol{g}}(\bar u + \Delta u)$是目标真实导向矢量；${{\boldsymbol{g}}_{\text{o}}}$是待计算余弦相似度的导向矢量。

图7是不同失配情况下全增量线性化模型、实际导向矢量的角度余弦相似曲线。可以看出，在3 dB波束宽度内，全增量线性化模型与真实导向矢量之间归一化相关性可达到0.95以上，而未估计目标余弦位移偏差的实际导向矢量与真实导向矢量之间相似度急剧衰减。因此，综合图7与上述不同失配情况下的检测概率曲线可得，本文全增量线性化模型在一定范围内可有效估计目标信息，减弱与真实导向矢量的失配，有较好的检测性能和抗失配稳健性；而实际导向矢量会随着失配情况的不同导致相似度的剧烈衰减，引起检测性能的波动。

图8是不同失配情况下本文所提检测器和对比检测器在不同训练数据K下的检测曲线，其中训练数据量从一维阵列的系统维度$N = 8$到大于系统维度的两倍$2N = 16$。图8 (a)显示在训练数据量较少的情况下，本文所提的PCSFIL-OM和PCSFIL-TM检测器的检测性能基本一致，均保持了较高的检测概率与较好的稳健性。随着K增大，所有检测器的检测概率开始增加，然而本文所提检测器的检测性能仍优于其他对比检测器，特别是训练数据量较少($K < 2N$)时，本文所提检测器和其他对比检测器的${P_{\text{d}}}$最大可相差0.8左右。图8 (b)显示当$\Delta u = 0.5$时，PCSFIL-OM和PCSFIL-TM的检测概率曲线仍然保持最高，无失配探测器GLRT和AMF的${P_{\text{d}}}$低于GLRT-LAM和GLRT-LAM-AMF，检测器SD和GLRT的检测概率最低。综合图8中不同训练数据K下的检测概率曲线，在训练数据量不充足、导向矢量失配的情况下，本文所提出检测器的检测性能皆优于其他检测器，并且在训练数据有限时，检测性能衰减的幅度较小。

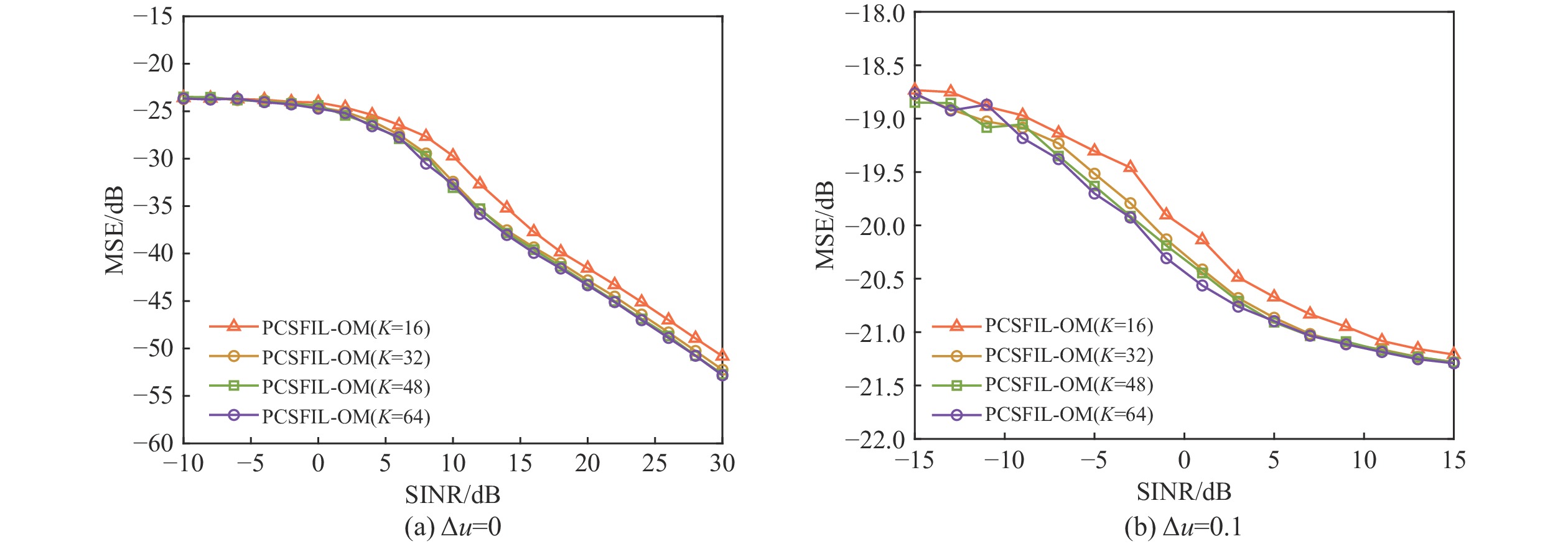
为了验证本文所提检测器的方位估计性能，引入均方误差：

式中：${R_{\text{M}}}$是蒙特卡洛实验次数；$\Delta u$是真实目标余弦偏移量；$\hat \Delta {u_{{\text{PD}}}}$是估计的目标余弦偏移量。

图9(a)和(b)分别是目标余弦偏移量为0和0.1时本文所提检测器的MSE曲线。从图9(a)可以看出，随着训练样本数增多，本文所提检测器的MSE曲线下降增快。但是当训练样本数$K > 2N$时，所提检测器的MSE曲线逐渐接近。从图9(b)可以看出，相比于图9(a)，在同样SINR下其MSE值较高，但随着训练数据量增大MSE也逐渐降低，最终趋于$-{\text{21 dB}}$。综合图9中MSE曲线可得，本文所提检测器在不同的导向矢量失配情况下，都具有较好的方位估计性能，一定范围内训练样本越多其MSE曲线的下降收敛速度越快。

图  7  不同失配情况下全增量线性化模型、实际导向矢量的角度余弦相似曲线

Fig.  7  Angular cosine similarity curves for fully incremental linearized models, real guiding vectors for different mismatches

下载: 全尺寸图片 幻灯片

图  8  不同失配情况下各检测器的检测曲线

Fig.  8  Detection curves of each detector for different mismatches

下载: 全尺寸图片 幻灯片

图  9  不同失配情况下本文检测器的MSE曲线

Fig.  9  MSE curves of the proposed detectors for different mismatches

下载: 全尺寸图片 幻灯片

4   结　论

本文提出了协方差结构辅助的全增量线性化模型自适应目标检测方法。该方法采取联合处理思想，充分利用噪声协方差的双对称结构的信息，在目标信息不准确情况下，通过阵列导向矢量建模为全增量线性化模型，然后利用酉矩阵变换设计协方差结构辅助的检测，通过将该检测问题转化为分数优化问题并白化处理推导出最终检测统计量，从而实现对目标的有效检测。基于仿真数据的实验结果表明，本文方法相较于传统检测方法在训练样本不足和目标信息不准确时皆具有更好的检测性能，可有效改善目标在复杂敏感环境下的检测性能。未来研究工作将基于其他检测准则设计检测器，以及不同环境下的小样本检测器设计。