Stretching transform jamming and characteristics of linear frequency modulation radar signal
-
摘要:
随着数字射频存储器(digital ratio frequency memory, DRFM)的成熟发展与广泛应用,基于DRFM的相干转发干扰成为当前雷达干扰技术的主流。相干转发干扰具有转发效率高、相干性强等突出优势,并且在数字域的处理算法灵活高效,能够产生复杂多样的干扰效果。但经过大量实践发现,当需要产生大范围连片干扰效果时,若干扰机采用密集转发,不但使DRFM运算量急剧增加,而且会破坏恒模约束,导致干扰机功放效率严重下降。基于该情况,本文提出了线性调频(linear frequency modulation,LFM)雷达信号的拉伸变换干扰方法:在数字域对雷达信号的脉宽、带宽分别压缩、展宽,即拉伸变换,再将其辐射至雷达接收机。拉伸信号经匹配滤波处理后,会呈现大范围连片相干干扰效果,干扰效果受拉伸变换因子影响,灵活可调,且拉伸变换干扰满足恒模约束。
Abstract:With the mature development and wide application of digital ratio frequency memory (DRFM), DRFM-based coherent forwarding jamming has become the mainstream of radar jamming technology. Coherent forwarding jamming has the outstanding advantages of high forwarding efficiency and strong coherence, and the processing algorithm in the digital domain is flexible and efficient, which can produce complex and diverse jamming effects. However, after a lot of practice, it is found that when it is necessary to produce a large-scale continuous interference effect, if the jammer adopts dense forwarding, it will not only increase the amount of DRFM computation sharply, but also destroy the constant mode constraint, resulting in a serious decrease in the power amplifier efficiency of the jammer. Based on this situation, this paper proposes a tensile transformation jamming method for linear frequency modulation (LFM) radar signals, which compresses and broadens the pulse width and bandwidth of radar signals in the digital domain, i.e., tensile transformation, and then radiates them to the radar receiver. After the tensile signal is processed by matching filtering, it will present a large-scale continuous coherent interference effect, which is affected by the tensile transformation factor, which is flexible and adjustable, and the tensile transformation interference satisfies the constant mode constraint.
-
0 引 言
新体制雷达综合运用多种抗干扰技术,尤其是采用脉内或脉间相干的信号波形,能够获得极高的相干处理增益,显著提高了雷达抗干扰能力[1-3]。因此,雷达干扰技术的研究是雷达电子战中永恒的课题。近年来,随着数字射频存储器(digital ratio frequency memory, DRFM)的快速发展,能够高效实现脉内调制信号的相干存储和转发,基于DRFM产生的干扰信号可以视为雷达信号的相干复制品[4-5],故而,DRFM在电子战中得到了广泛的应用,同时使得相干转发干扰技术得到了蓬勃发展[6-9]。
目前典型干扰包括间歇采样转发干扰[10-13]、移频转发干扰[14-16]等,均得到了持续发展和广泛应用。目前,以间歇采样转发干扰为主流干扰,采用收发分时体制,极大地解决了天线收发隔离难题,且能产生导前假目标。但在实际应用中,现有针对相干转发干扰研究的不足之处逐渐凸显:1)目前针对相干转发干扰的研究多基于已有干扰进行二次调制,如在间歇采样转发干扰的基础上,发展出间歇采样移频转发干扰、间歇非均匀采样转发干扰[17-21]等,未打破常规干扰模型;2)相干转发干扰产生离散点目标串,对真实目标的遮盖效果不够完美,容易把真目标漏出来;3)当需要得到大范围连片遮盖效果时,干扰机需要对相干转发干扰做密集重复转发,不仅使得DRFM运算处理的数据量突增,而且合成的干扰波形严重偏离恒模约束,导致干扰机功放效率和资源的巨大浪费。因此,研究一种具有大范围连片遮盖效果的相干干扰具有重要意义。
为解决上述问题,近年来,很多学者从不同角度开展研究:文献[22]研究了一种针对合成孔径雷达的调频率失配脉间去相干法,即改变线性调频(linear frequency modulation,LFM)信号的频率,使干扰信号与雷达信号调频率失配,干扰信号经脉压后输出波形在距离维出现扩散现象。文献[23]进一步分析推导了频率调制对LFM信号脉压输出幅度和宽度的影响,包括匹配滤波器和加权滤波器两种情况。在上述基础上,文献[24]将调频斜率失配方法应用于干扰通信一体化设备,并在通信接收端进行去斜处理和快速傅里叶变换,不仅能够产生压制干扰效果,还具有高速率通信数据传输能力。文献[25-26]研究了干扰机对雷达信号进行锯齿波调频、正弦调频,再经放大后转发,可以产生假目标干扰和遮盖干扰。文献[27-30]研究了多相位分段调制干扰,对信号不同时间分段调制不同相位值,得到对应的干扰信号,通过破坏部分和保留原雷达信号的相干性实现局部遮盖干扰。文献[31-32]分别研究了灵巧噪声卷积调制干扰和乘积调制干扰,实现了干扰距离向和方位向的二维覆盖和灵活控制。
但上述研究仍存在不足之处:文献[22-24]没有从数字域处理的角度进行全面的分析以及规律性的总结,没有深入挖掘调频斜率失配干扰的效果;文献[25-26]处理方法复杂,在工程上难以实现,且压制区域呈现两端高、中间低的趋势,内部空隙多,无法产生连续的干扰效果;文献[27-30]需要通过更多的分段数获得更宽的压制区域,运算量大幅增加,且压制区域呈现中间高、两侧递减的趋势,无法形成大范围、相对平坦的干扰电平;文献[31-32]所提方法仅有压制效果,干扰输出形式较为单一,调制复杂,并且能量利用率提高是以压制范围为代价的。
鉴于此,本文提出一种对LFM雷达信号的拉伸变换干扰方法,其核心思想是将干扰机接收的雷达信号在数字域进行时间尺度拉伸变换后,再将其辐射返回雷达接收机,经脉压处理后,输出信号主瓣急剧展宽,在时域维实现区域遮盖的效果,达到产生“大面积连片相干干扰”的目的,并且能够满足恒模约束。由于拉伸变换干扰通过数字域的抽取、内插实现,其应用范围不限于LFM信号,亦可用于相位编码等其他体制的信号。从干扰角度而言,拉伸变换干扰是高效的、底层的处理方式。
1 拉伸变换数学模型
1.1 拉伸变换的定义
信号x(n)在数字域经过抽取、内插等基本运算,变换为新的序列y(n)=x(αn),拉伸因子α决定拉伸变换的程度。假使信号x(n)的长度为N点,采样率为fs,则信号时长τx=N/Nfsfs;若保持采样率不变,那么,变换后的信号y(n)的长度M=N/Nαα点,信号时长τy=M/Mfsfs。即通过数字域的抽取或内插,使信号在时域维压缩或展宽。将输入信号x(n)映射成输出信号y(n)=x(αn)的变换或运算定义为拉伸变换,并用拉伸域描述拉伸变换输出信号以及拉伸变换特性。
1.2 拉伸变换模型
通常,雷达发射LFM信号可表示为
st(t)=rect(tTp)ejπKt2 (1) 式中:Tp为信号脉宽(pulse width, PW);rect(t/Tp)={1,|t|⩽;K = {B}/{{{T_{\text{p}}}}}为调频斜率。
本文分别从两种情况考虑雷达发射LFM信号的拉伸变换:1)为保证带宽(band width, BW)不变,拉伸PW,即时域维的拉伸变换;2)为保证PW不变,拉伸BW,即频域维的拉伸变换。
1.2.1 时域拉伸模型
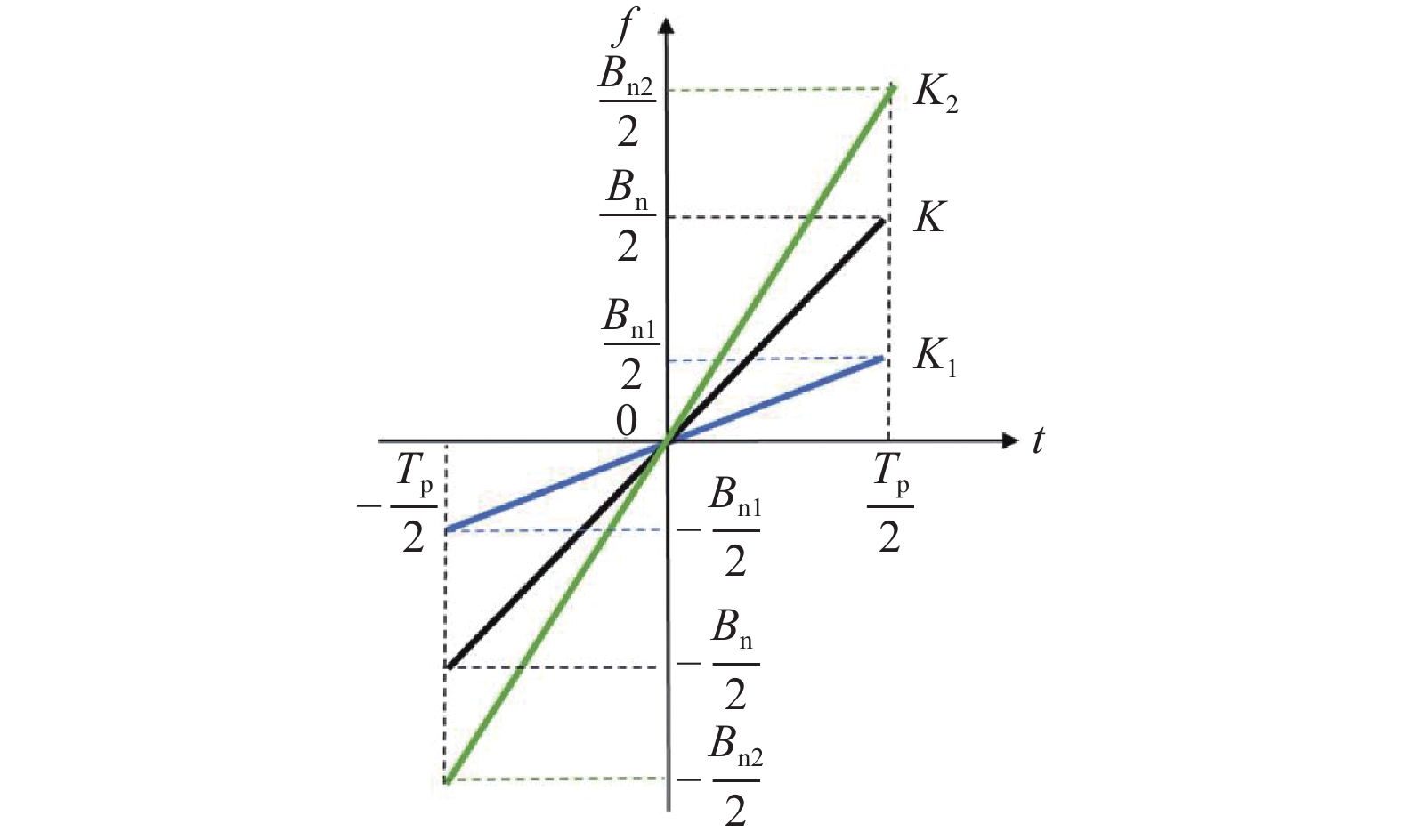
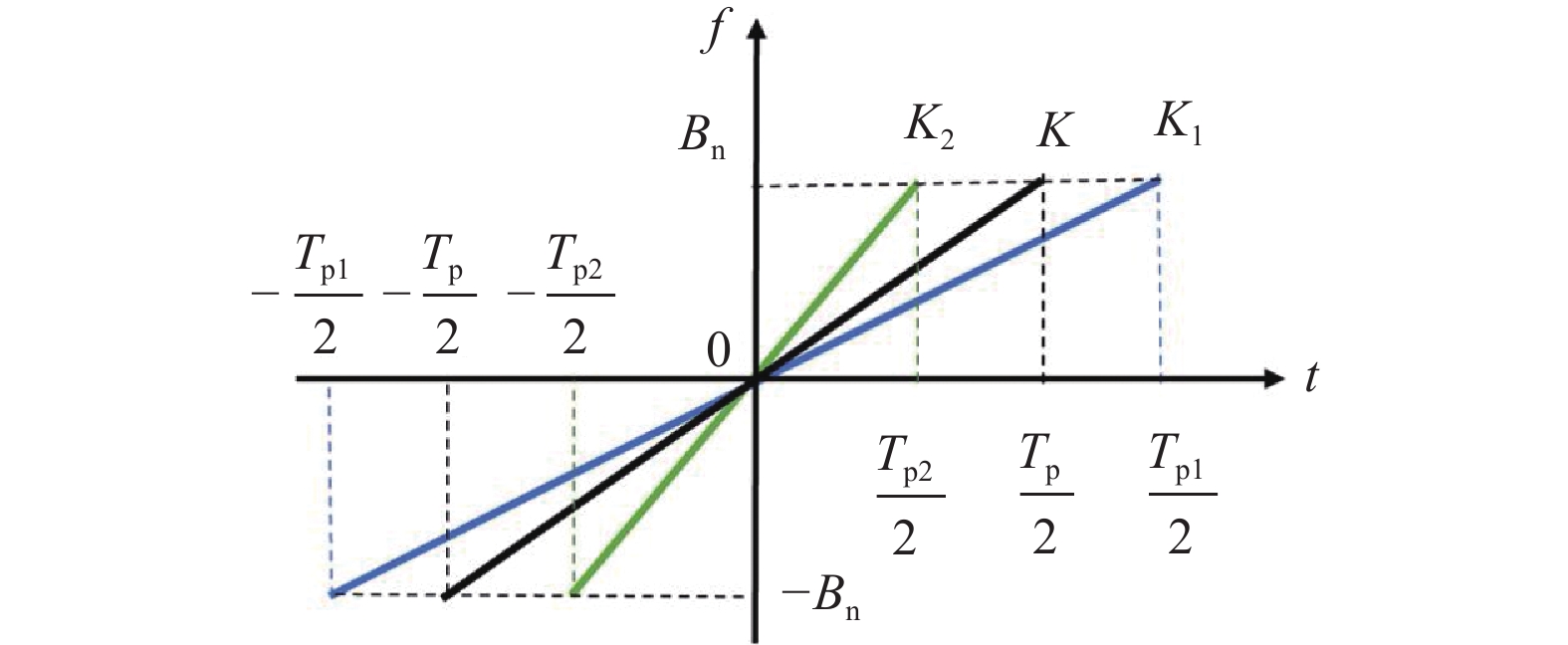
信号在时域维进行拉伸变换,如图1所示,时域拉伸信号可表示为
s_{\mathrm{J}}^{\mathrm{PW}}\left(t\right)=\text{rect}\left(\frac{t}{T_{{\mathrm{p}}\alpha}}\right)\mathrm{e}^{\mathrm{j}\text{π}K_{\alpha}t^2} (2) 式中:{T_{{\text{p}}\alpha}} = {{{T_{\text{p}}}} \mathord{\left/ {\vphantom {{{T_{\text{p}}}} \alpha }} \right. } \alpha }为拉伸后的信号PW,拉伸因子\alpha \in \left( {0,\infty } \right);{K_{ \alpha }} = \alpha K为拉伸后的调频斜率。图1中,斜率{K_1}对应\alpha \in \left( {0,1} \right),斜率{K_2}对应\alpha \in \left( {1,\infty } \right)。
将拉伸信号s_{\mathrm{J}}^{{\mathrm{PW}}}\left(t\right)送入匹配滤波器进行脉压处理,输出信号 y_{\mathrm{J}}^{{\mathrm{PW}}}\left(t\right) 写成幅度和相位的形式,即
y_{\mathrm{J}}^{\mathrm{PW}}\left(t\right)=\mathrm{e}^{-\mathrm{j} {\text{π}} K t^2}\int\limits_{ - \infty }^\infty {A}\left(\tau\right) \mathrm{e}^{\mathrm{j}\left({\text{π}}\left(K_{ \alpha }-K\right) \tau^2+2 {\text{π}} K t \tau\right)} \mathrm{d} \tau (3) 式中, A\left(\tau \right) 为信号包络的有限支撑域。
令\varphi\left(\tau, t\right)={\text{π}}\left(K_{ \alpha }-K\right) \tau^2+2 {\text{π}} K t \tau为信号的相位函数,采用驻相原理对式(3)进行推导,得到时域拉伸情况下拉伸变换信号脉压输出表达式近似为
{y}_{{\mathrm{J}}}^{{\mathrm{PW}}}\left(t\right)\approx \sqrt{\frac{1}{\left(1-\alpha \right)K}}{\text{e}}^{\text{j}\left(\tfrac{\text{π}\alpha K}{1-\alpha }{t}^{2}-\tfrac{\text{π}}{\text{4}}\right)},-\frac{\left(1-\alpha \right){T}_{\text{p}}}{2\alpha } < t < \frac{\left(1-\alpha \right){T}_{\text{p}}}{2\alpha } (4) 1.2.2 频域拉伸模型
图2所示为频域维的拉伸变换,频域拉伸信号可表示为
s_{\mathrm{J}}^{\mathrm{BW}}\left(t\right)=\operatorname{rect}\left(\frac{t}{T_{\mathrm{p}}}\right) \mathrm{e}^{\mathrm{j} {\text{π}} K_{ \alpha } t^2} (5) 式中, {K_{ \alpha }} = \alpha {B_{\mathrm{n}}}/T_{\mathrm{P}} 为拉伸后的信号BW。图2中,斜率{K_1}对应\alpha \in \left( {0,1} \right),斜率{K_2}对应\alpha \in \left( {1,\infty } \right)。
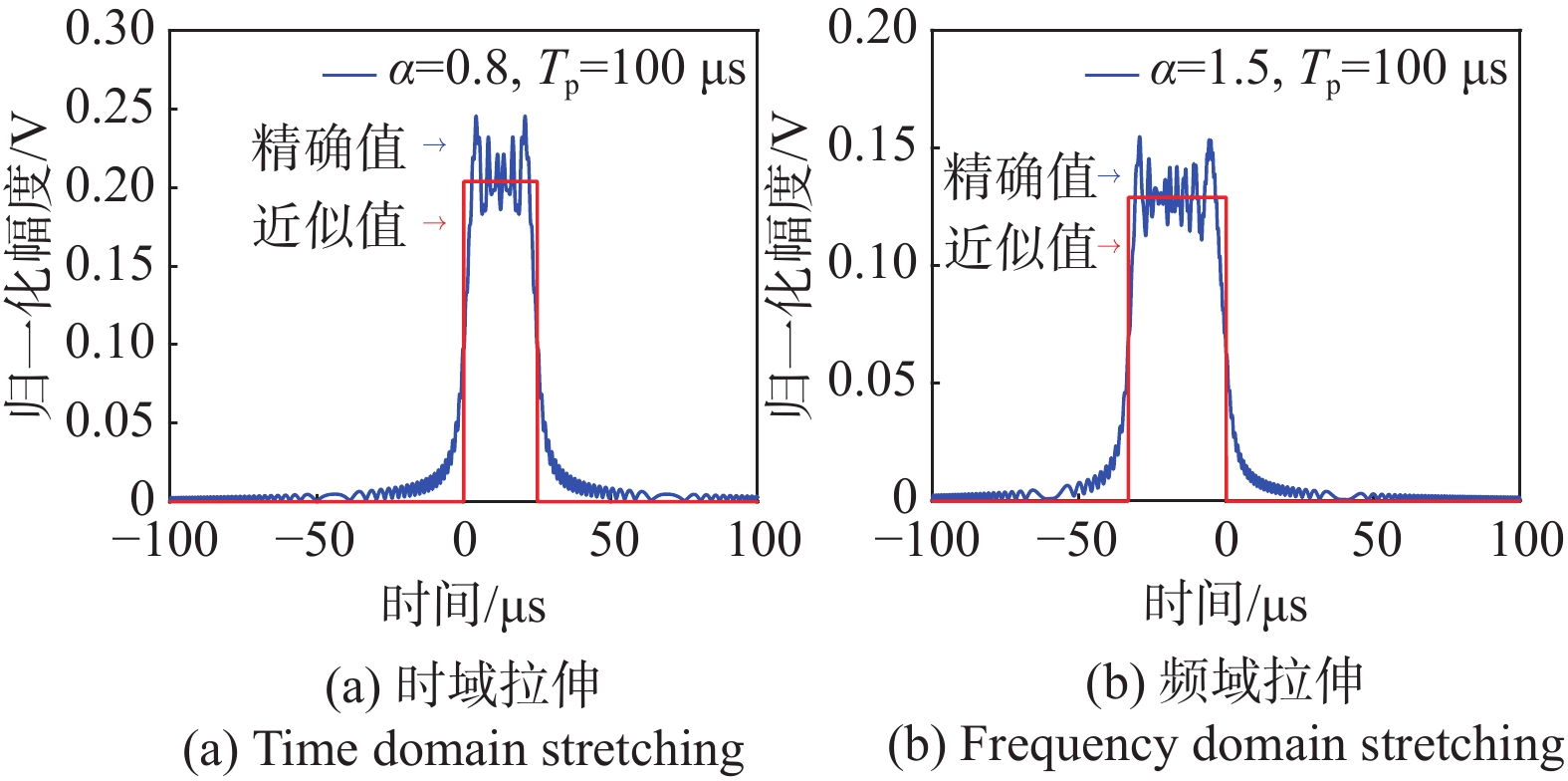
将拉伸信号 s_{\mathrm{J}}^{{\mathrm{BW}}}\left(t\right) 送入雷达的匹配滤波器进行脉压处理,与1.2.1节推导方法类似,得到频域拉伸情况下,拉伸变换信号脉压输出表达式近似为
y_{\mathrm{J}}^{\mathrm{BW}}\left(t\right) \approx \begin{cases}\sqrt{\dfrac{1}{\left(1-\alpha\right) K}} \mathrm{e}^{\mathrm{j} \tfrac{{\text{π}} \alpha K}{1-\alpha} t^2-\mathrm{j} \tfrac{{\text{π}}}{4}}, \quad t \in\left(-\dfrac{1-\alpha}{2} T_{\mathrm{p}}, \dfrac{1-\alpha}{2} T_{\mathrm{p}}\right), & 0 <\alpha <1 \\ \sqrt{\dfrac{1}{\left(1-\alpha\right) K}} \mathrm{e}^{\mathrm{j} \tfrac{{\text{π}} \alpha K}{1-\alpha} t^2-\mathrm{j} \tfrac{{\text{π}}}{4}}, \quad t \in\left(-\dfrac{\alpha-1}{2 \alpha} T_{\mathrm{p}}, \dfrac{\alpha-1}{2 \alpha} T_{\mathrm{p}}\right), & \alpha >1\end{cases} (6) 图3给出了上述拉伸信号的近似表达式与精确值的对比结果。式(4)及式(6)表明,当时域拉伸在 \pm(1-\alpha) T_{\mathrm{p}} / (2 \alpha)(\alpha >0) 范围内,频域拉伸在 \pm(1-\alpha) T_{\mathrm{p}} / 2 \left(0 < \alpha < 1\right) 和 \pm {{\left( {\alpha - 1} \right){T_{\mathrm{p}}}} \mathord{\left/ {\vphantom {{\left( {\alpha - 1} \right){T_p}} {2\alpha }}} \right. } ({2\alpha })}\left(\alpha > 1\right) 范围内时,拉伸信号脉压输出 \left| {y_{\mathrm{J}}^{{\mathrm{PW}}}\left(t\right)} \right| 和 \left| {y_{\mathrm{J}}^{{\mathrm{BW}}}\left(t\right)} \right| 具有恒定值,而在该范围外为零,图3满足此条件。
2 拉伸干扰脉压特性分析
原始雷达信号的匹配滤波输出呈现“极窄尖峰状”,由于拉伸变换信号与雷达接收机一定程度上非匹配,因此,拉伸变换信号脉压输出主瓣展宽,幅度降低,由“极窄尖峰状”扩散为“宽板凳状”,形成准等幅连片的效果。基于上述特点,将拉伸变换应用于雷达电子干扰:干扰机对雷达信号进行拉伸变换,再将拉伸变换干扰放大转发至雷达接收机进行信号处理,能够实现满足恒模约束的大范围连片干扰效果。
本节将脉压输出峰值下降4 dB的位置定义为泛主瓣区,分析拉伸变换干扰脉压输出主瓣展宽区域的宽度、幅度,得出可控干扰变换规律。
2.1 泛主瓣区宽度特性
时域拉伸情况下,由式(4)得到拉伸干扰经脉压输出的泛主瓣区宽度为
\tau _{\mathrm{J}}^{{\mathrm{PW}}} = \frac{{\left| {1 - \alpha } \right|}}{\alpha }{T_{\text{p}}} (7) 由于匹配滤波输出的主瓣宽度为 {\tau _0} = 1/{B_{\text{n}}} ,则拉伸干扰覆盖的距离单元数为
\Delta R_{\text{c}}^{{\mathrm{PW}}} = \frac{{\tau _{\mathrm{J}}^{\mathrm{PW}}}}{{{\tau _0}}} = \frac{{\left| {1 - \alpha } \right|}}{\alpha }{B_{\text{n}}}{T_{\text{p}}} (8) 频域拉伸情况下,当拉伸因子\alpha \in \left( {0,1} \right)时,由式(6)得到泛主瓣区宽度及覆盖距离单元数为:
\tau\mathrm{_J^{\mathrm{BW}}}=\left(1-\alpha\right)T_{\text{p}} (9) \Delta R_{\text{c}}^{{\mathrm{BW}}} = \frac{{\tau _{\mathrm{J}}^{{\mathrm{BW}}}}}{{{\tau _0}}} = \left(1 - \alpha \right){B_{\text{n}}}{T_{\text{p}}} (10) 当拉伸因子\alpha \in \left( {1,10} \right)时,泛主瓣区宽度及覆盖距离单元数为:
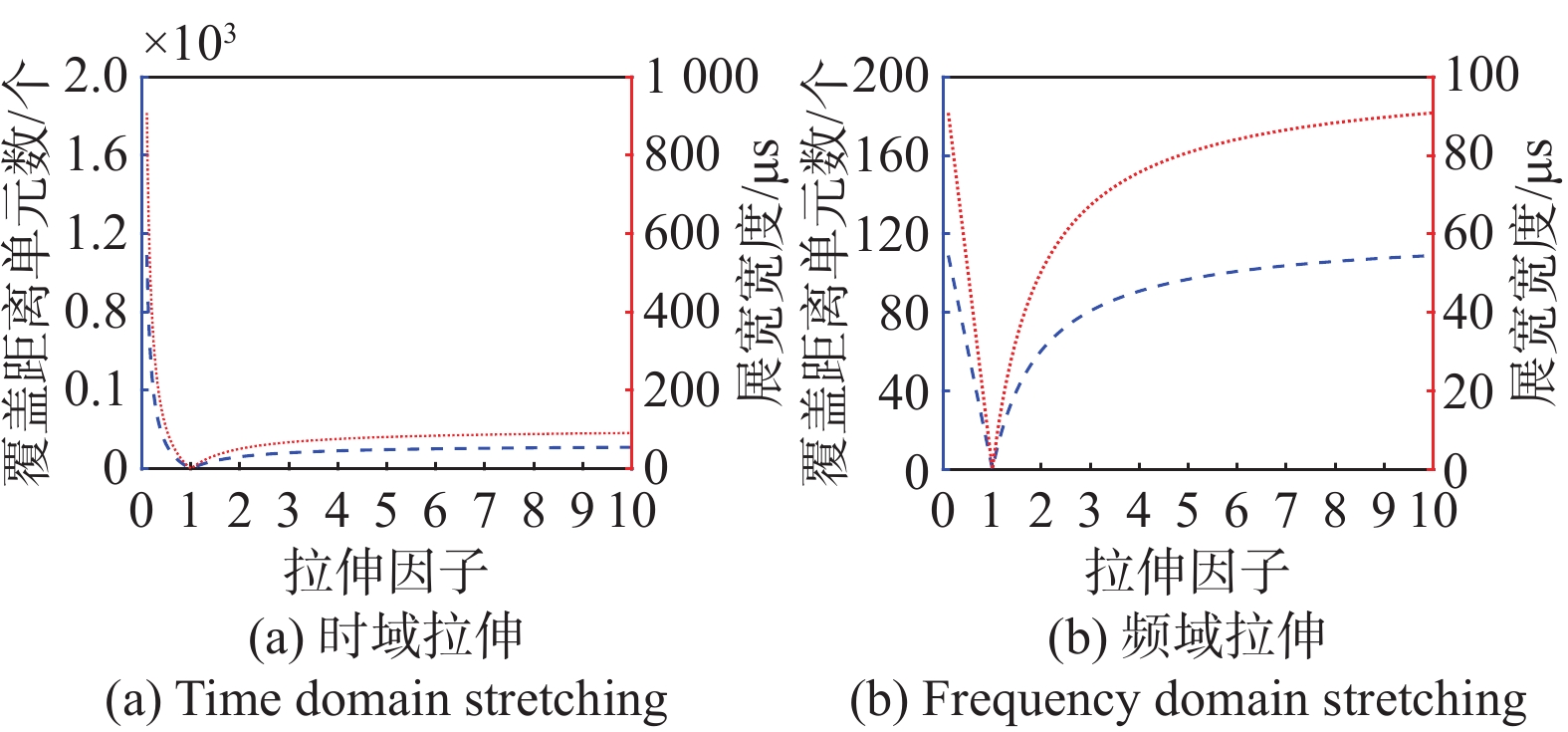
\tau _{\mathrm{J}}^{{\mathrm{BW}}} = \frac{{\alpha - 1}}{\alpha }{T_{\text{p}}} (11) \Delta R_{\text{c}}^{{\mathrm{BW}}} = \frac{{\tau _{\mathrm{J}}^{{\mathrm{BW}}}}}{{{\tau _0}}} = \frac{{\alpha - 1}}{\alpha }{B_{\text{n}}}{T_{\text{p}}} (12) 总结式(7)~(12)如表1所示。可以看出:干扰覆盖范围由拉伸因子、信号BW、信号PW决定,其中,BW、PW与覆盖范围呈正向线性关系,并且为雷达信号自身特性,不受干扰机调控;干扰机通过控制拉伸因子,即可控制干扰信号覆盖范围。因此,需要进一步讨论拉伸因子对干扰覆盖范围的影响。
图4给出时域拉伸和频域拉伸情况下,拉伸因子对泛主瓣区宽度的影响,其中,设置信号BW {B_{\mathrm{n}}} = 1.2\;{\text{MHz}},信号PW {T_{\text{p}}} = 100\;{\text{μs}}。图4(a)中,当拉伸因子\alpha \in \left( {1,10} \right)时,泛主瓣区缓慢展宽,趋于固定值;当拉伸因子\alpha \in \left( {0,1} \right)时,泛主瓣区快速展宽,且展宽范围远大于\alpha \in \left( {1,10} \right)情况。图4(b)中,拉伸因子\alpha \in \left( {0,1} \right)及\alpha \in \left( {1,10} \right)时,泛主瓣区最大展宽宽度与变化速度均近似。相比时域拉伸情况,频域拉伸的泛主瓣区展宽范围更小。以时域拉伸为例,拉伸因子\alpha = 0.7,干扰覆盖距离单元达到52个,干扰覆盖真实范围为6.5 km,说明通过拉伸变换能够实现灵活可控的“大范围连片”干扰效果。
表 1 变化规律公式Tab. 1 Formula for changing patterns拉伸因子 泛主瓣区域
展宽宽度 {\tau _{\mathrm{J}}}覆盖距离单元数 \Delta {R_{\text{c}}} \alpha \in \left( {0,\infty } \right) \tau _{\mathrm{J}}^{{\mathrm{PW}}} = \dfrac{{\left| {1 - \alpha } \right|}}{\alpha }{T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{PW}}} = \dfrac{{\left| {1 - \alpha } \right|}}{\alpha }{T_{\text{p}}}{B_{\text{n}}} \alpha \in \left( {0,1} \right) \tau _{\mathrm{J}}^{{\mathrm{BW}}} = \left(1 - \alpha \right){T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{BW}}} = \left(1 - \alpha \right){T_{\text{p}}}{B_{\text{n}}} \alpha \in \left( {1,\infty } \right) \tau _{\mathrm{J}}^{{\mathrm{BW}}} = \dfrac{{\alpha - 1}}{\alpha }{T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{BW}}} = \dfrac{{\alpha - 1}}{\alpha }{T_{\text{p}}}{B_{\text{n}}} 2.2 泛主瓣区幅度特性
根据式(4)和(6),对脉压输出信号 y_{\mathrm{J}}^{{\mathrm{PW}}}\left(t\right) 和 y_{\mathrm{J}}^{{\mathrm{BW}}}\left(t\right) 取模,可得泛主瓣区幅值为
\left| {y_{\mathrm{J}}^{}\left(t\right)} \right| = \sqrt {\frac{1}{{\left| {1 - \alpha } \right|K}}} = \sqrt {\frac{{{T_{\mathrm{p}}}}}{{\left| {1 - \alpha } \right|{B_{\mathrm{n}}}}}} (13) 与匹配滤波输出相比,拉伸干扰经脉压输出的泛主瓣区幅值变化倍数为
{r_{{\text{mag}}}} = \frac{{\left| {{y_{\mathrm{J}}}\left(t\right)} \right|}}{{{T_{\mathrm{p}}}}} = \sqrt {\frac{1}{{\left| {1 - \alpha } \right|{B_{\mathrm{n}}}{T_{\mathrm{p}}}}}} (14) 泛主瓣区功率变化分贝值为
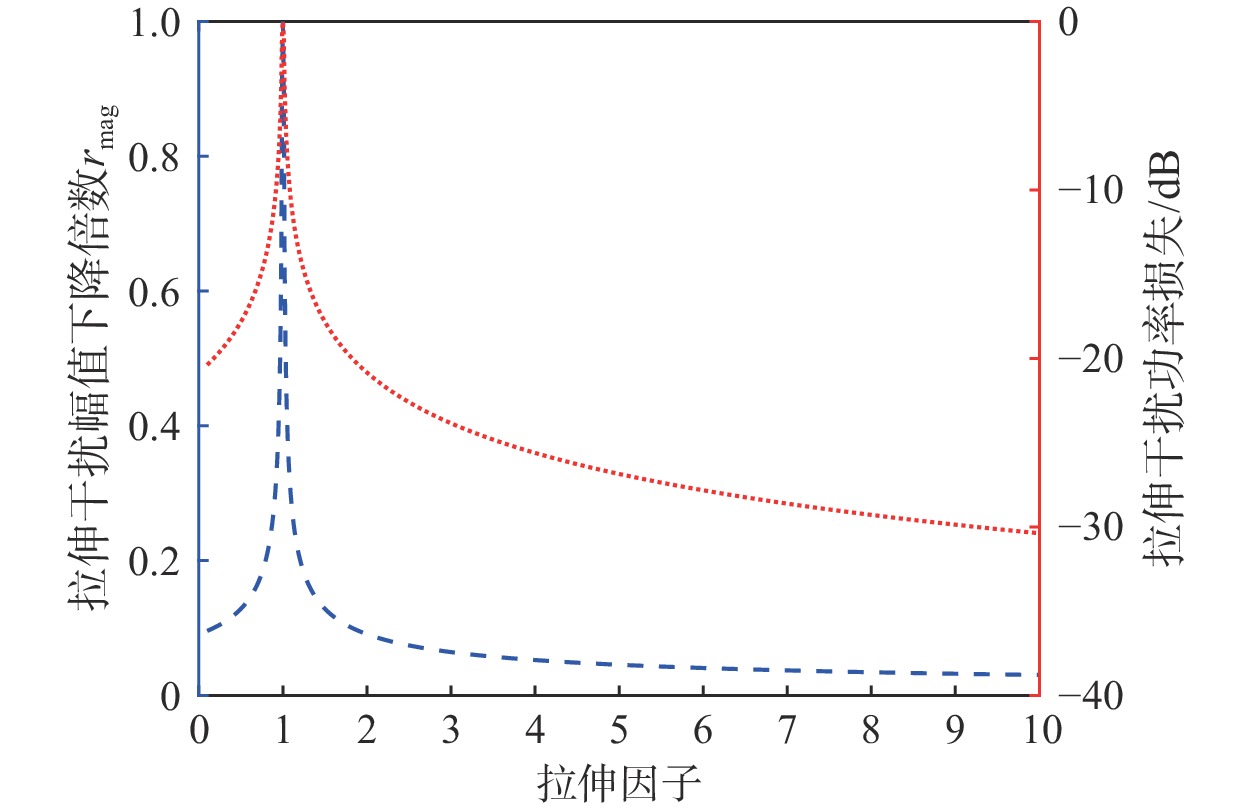
{r_{{\text{power}}}} = 20\lg {r_{{\text{mag}}}} = - 10\lg \left(\left| {1 - \alpha } \right|{B_{\mathrm{n}}}{T_{\mathrm{p}}}\right) (15) 由式(13)~(15)可知,脉压输出信号幅值 \left| {y_{\mathrm{J}}^{}\left(t\right)} \right| 、幅值下降倍数 {r_{{\text{mag}}}} 、功率下降倍数 {r_{{\text{power}}}} 和拉伸程度 \left| {1 - \alpha } \right| 、雷达信号BW {B_{\mathrm{n}}} 、PW {T_{\mathrm{p}}} 均成反比,拉伸程度每增加2倍,功率下降3 dB。
图5给出拉伸因子对泛主瓣区幅度的影响,其中,信号BW {B_{\mathrm{n}}} = 1.2\;{\text{MHz}},信号PW {T_{\text{p}}} = 100\;{\text{μs}}。以\alpha = 1为参考点,此时匹配滤波输出峰值幅度;当\alpha \in \left( {0,2} \right)时,幅值下降速率极高,当\alpha =0.9时,脉压输出功率降低10.8 dB,说明信号微小拉伸会带来功率快速降低。
根据能量守恒原则,信号覆盖范围扩散会带来幅值衰减,进而分析拉伸变换干扰脉压输出宽度和幅度的关系。由式(8)、(12)和(14)可知,在时域拉伸以及拉伸因子α∈(1,∞)的频域拉伸情况下,幅度和宽度关系为
r_{{\text{mag}}}^2 \cdot \Delta {R_{\text{c}}} = \frac{1}{\alpha } (16) 在拉伸因子α∈(0,1)的频域拉伸情况下,幅度和宽度关系为
r_{{\text{mag}}}^2 \cdot \Delta {R_{\text{c}}} = 1 (17) 可以看出,幅度的平方和宽度呈负相关,在式(16)情况下,幅度平方和宽度的乘积与拉伸因子有关。
综上,干扰覆盖区域的宽度和信号功率之间存在矛盾,因此,选择拉伸因子时需要综合考虑。
3 仿真验证
参考典型雷达,参数设置如表2所示,分析拉伸干扰经雷达匹配滤波器的输出特性,给出干扰效果的典型数值;然后使用恒虚警(constant false alarm rate,CFAR)检测器进行仿真实验,验证拉伸干扰的干扰效果。本节实验均以时域拉伸变换为例进行研究。
表 2 仿真参数设置Tab. 2 Simulation parameter settings参数 取值 雷达信号PW {T_{\text{p}}} 100\;{\text{μs}} 雷达信号BW {B_{\text{n}}} 1.2 MHz 采样率{f_{\text{s}}} 36 MHz 3.1 拉伸干扰脉压输出
图6给出了不同拉伸因子的拉伸干扰进入雷达接收机后经脉压输出的变化趋势。
图6(a)为不同拉伸因子时拉伸干扰脉压输出变化趋势,并以匹配滤波输出信号对拉伸干扰幅度进行归一化处理;图6(b)为图6(a)中信号幅度强度图,显示了泛主瓣区幅值大小以及覆盖范围、位置。由图6可以看出:1)拉伸干扰可以使雷达在距离维产生准等幅连片且范围可控的遮盖干扰,随着失配程度\left| {1 - \alpha } \right|增大,由“极窄尖峰状”扩散为“宽板凳状”; 2)泛主瓣区出现微弱抖动,抖动起伏不超过3 dB,且泛主瓣区中心对称;3)当拉伸因子\alpha < 1时,拉伸干扰滞后于真实回波信号,当拉伸因子\alpha > 1时,拉伸干扰超前于真实回波信号;4)与匹配滤波输出相比,干扰覆盖范围越宽,功率损失越大。
表3~4给出了{B_{\text{n}}} = 1.2\;{\text{MHz}}, {T_{\text{p}}}=100\;{\text{μs}}情况下拉伸因子对应的干扰效果。当信号进行微小拉伸变换,如拉伸因子为0.9,功率快速下降约10.8 dB,然后功率保持相对慢速持续下降,同时干扰覆盖范围快速扩张。
表 3 {\boldsymbol{\alpha \in \left( {0,1} \right)}}的干扰效果Tab. 3 The jamming effect of stretching factor {\boldsymbol{\alpha}} \in \left( {{\boldsymbol{0}},{\boldsymbol{1}}} \right)\alpha 干扰覆盖距离单元数/个 功率变化值/dB 0.9 13 -10.8 0.8 30 -13.8 0.6 80 -16.8 0.4 180 -18.6 表 4 {\boldsymbol{\alpha \in \left( {1,\infty } \right)}}的干扰效果Tab. 4 The jamming effect of stretching factor {\boldsymbol{\alpha }}\in \left( {{\boldsymbol{1}},{\boldsymbol{\infty}} } \right)\alpha 干扰覆盖距离单元数/个 功率变化值/dB 1.1 10 -10.8 1.2 20 -13.8 1.4 34 -16.8 1.6 45 -18.6 从表3~4可以看出:\alpha =0.9 或1.1时,功率损失较小,但覆盖范围有限;拉伸因子\alpha \in \left[ {0.6,0.9} \right) \cup \left( {1.1,1.4} \right]时,功率损失可控且覆盖范围广;拉伸因子 \alpha \in \left(0,0.6\right) \cup \left( {1.4,\infty } \right) 时,虽覆盖范围极广,但功率损失严重;当\left| {1 - \alpha } \right|值一致时,拉伸干扰损失功率相同,但拉伸因子\alpha \in \left( {0,1} \right)的信号展宽宽度远大于\alpha \in \left( {1,\infty } \right)时。因此,在实际应用中,综合考虑覆盖范围和功率损失,常选用\alpha \in \left[ {0.6,0.9} \right]以及\alpha \in \left[ {1.1,1.4} \right]的拉伸干扰。
3.2 拉伸干扰对CFAR检测的影响
CFAR检测器通常针对“单目标”或者“点目标”设计,在CFAR检测器中,单元平均CFAR(cell averaging CFAR, CA-CFAR)具有在均匀杂波环境下背景噪声估计准确、计算复杂度低等优势,因此,本节用CA-CFAR为测试大面积干扰对点目标的遮盖效果进行实验验证。参数设置如下:虚警概率{P_{{\text{fa}}}}为{10^{ - 6}},噪声功率{P_{\text{n}}}为1 W,信噪比(signal-to-noise ratio, SNR)为10 dB,参考单元个数为32。
3.2.1 拉伸干扰对CA-CFAR检测门限的影响
本节分析所提干扰方法经过CA-CFAR检测器后检测门限的变化趋势。
考虑覆盖范围和功率下降的情况,分别取\alpha = 0.7、1.3、0.4,干噪比(jamming-to-noise ratio, JNR)为25 dB,由虚警概率得出门限因子\eta = 15.4,将门限因子与参考单元功率相乘得到门限变化,结果如图7所示。
图7 (a)中无干扰时,在第60个距离单元处检测到目标信号;图7(b)、(c)中,拉伸因子 \alpha = 0.7 、 1.3 ,拉伸干扰抬升了51个、27个距离单元内的检测门限,对应到真实场景中干扰覆盖区域分别为7.7 km和4 km,相比于无干扰时该情况下门限电平均抬升了约40 dB,能够形成大面积连片干扰效果,在CA-CFAR检测器中遮盖真实目标。图7(d)中,拉伸因子为0.4,由于拉伸干扰失配程度严重,干扰覆盖180个距离单元,门限电平仅抬升约20 dB,同等干扰功率下无法遮盖目标,需要更大的干扰功率才能有效遮盖真实目标。此外,对比图7(b),图7(c)中拉伸因子 \alpha > 1 使得拉伸干扰超前于目标位置。
综上所述,可以得出以下结论:1)综合考虑覆盖范围和门限抬升的情况, \alpha 取值约为0.7和 1.3 时能够同时兼顾覆盖范围及抬升电平,干扰效果较好;2)拉伸因子大于1或小于1,分别对应着超前、滞后真实目标的干扰效果。
3.2.2 拉伸干扰对CA-CFAR检测目标的影响
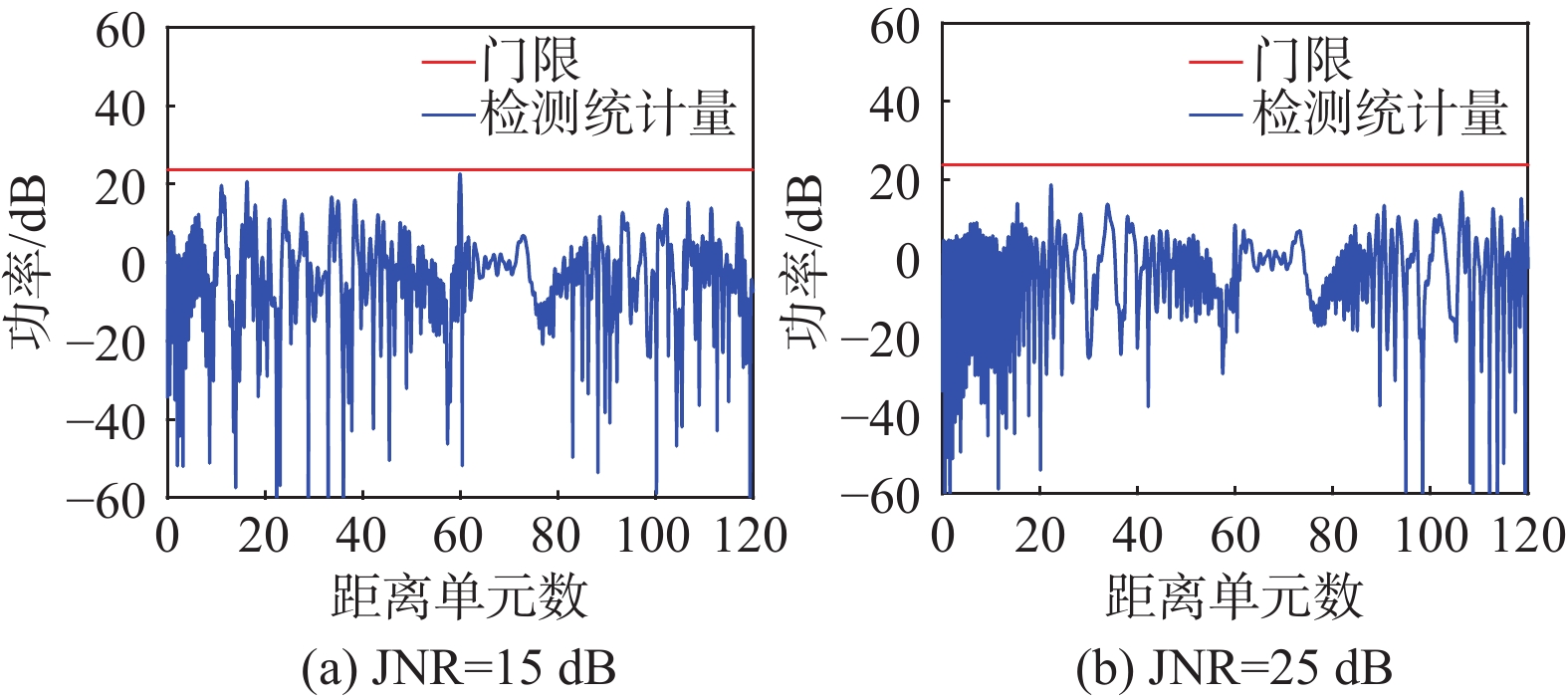
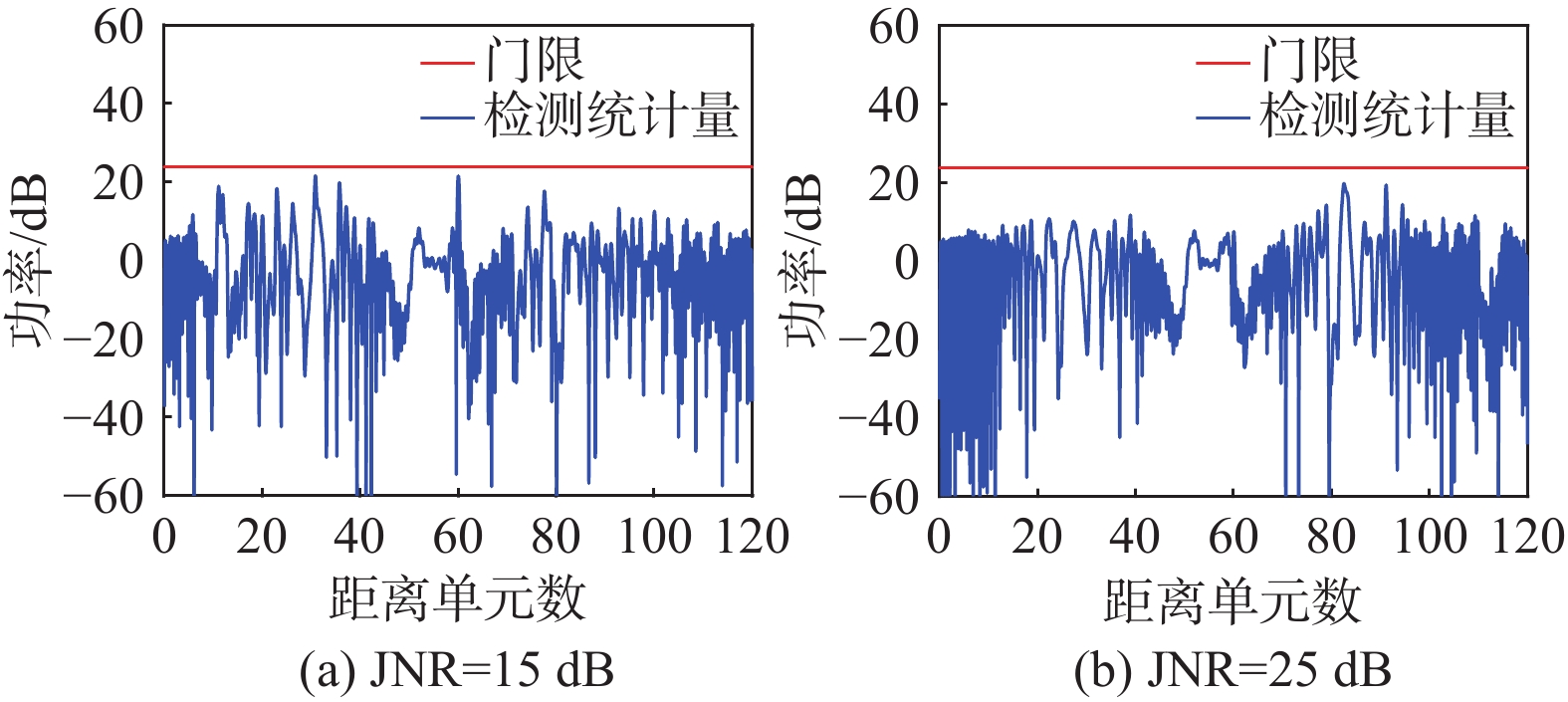
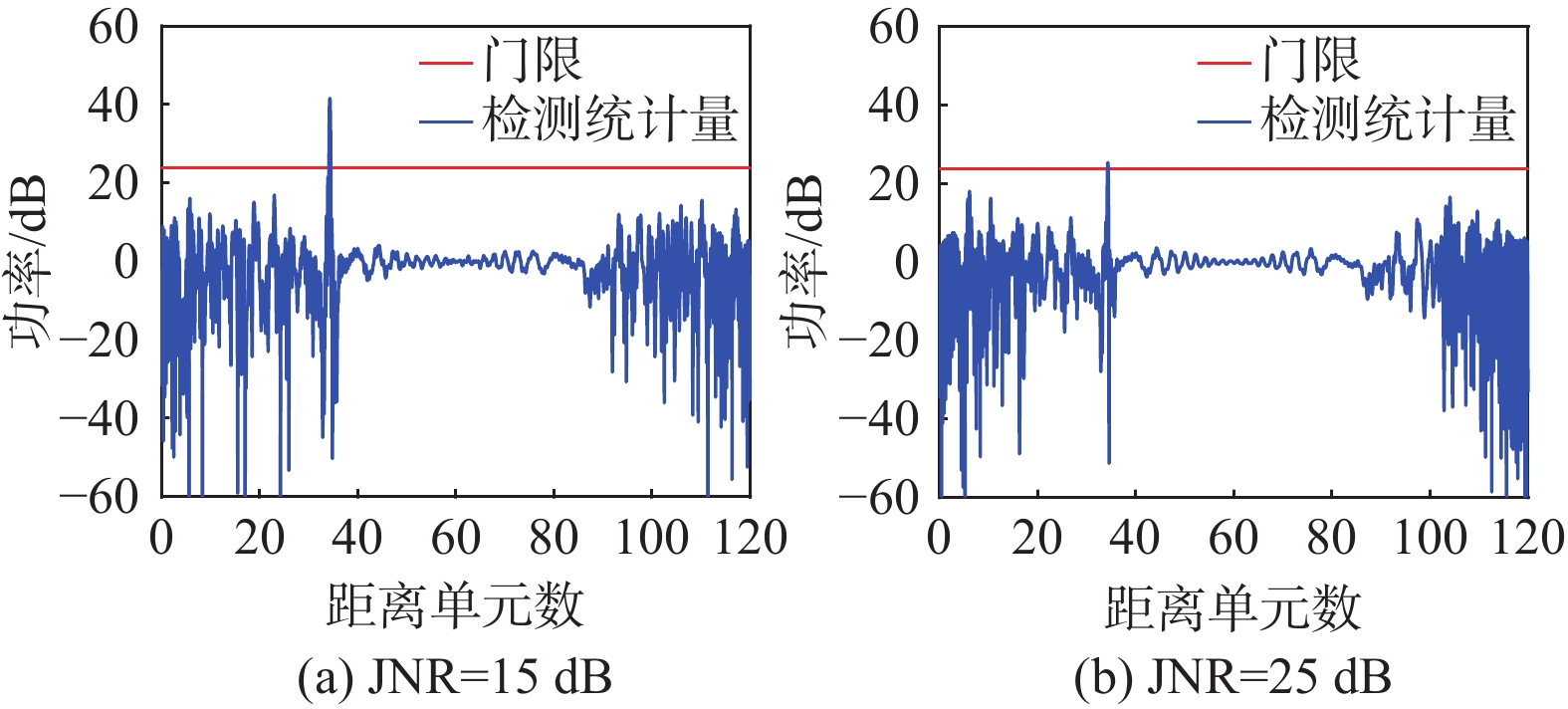
本节通过仿真实验分析拉伸干扰对CA-CFAR检测目标的影响。仿真参数如表2所示,综合考虑覆盖范围和功率下降的情况,本节取拉伸因子分别为\alpha = 1.2、0.8、0.4,JNR分别为JNR=15、25 dB,通过虚警概率得出对应固定门限值为 23.7\;{\text{dB}},设置检测统计量为检测单元功率与参考单元功率的比值,实验过程中,若检测统计量高于门限,则认为检出信号。仿真结果如图8~11所示。
图8无干扰情况下,第60个距离单元处检测统计量远高于门限值,检测到目标信号。图9和图10中,当施加拉伸干扰后,随着干扰信号功率增加,即JNR增大,参考单元功率抬升,真实目标附近的检测统计量逐渐低于检测门限,导致检测器无法检测到目标信号。拉伸因子\alpha = 0.8和\alpha = 1.2带来的功率下降值相同,但覆盖范围不同,\alpha = 0.8时的拉伸干扰覆盖范围更广,若在参考单元外产生假目标,则\alpha = 0.8时的假目标距离真实目标位置更远。图11拉伸因子\alpha = 0.4,干扰信号功率损失严重,参考单元功率抬升小,使干扰机辐射相对大的干扰功率,但目标信号仍暴露在检测门限外。
在上述仿真实验基础上,进行蒙特卡洛统计特性分析,得到施加不同拉伸因子产生的拉伸干扰在不同SNR下的检测概率,如表5所示,JNR=20 dB。
表 5 不同拉伸因子及SNR下的检测概率Tab. 5 Detection probability under different stretching factors and SNRSNR/ dB \alpha 0.7 0.8 1.2 1.3 0.4 −10 0.15 0.05 0.15 0.10 0.30 0 0.30 0.15 0.25 0.30 0.55 15 0.45 0.20 0.40 0.55 1.00 由表5可知,随着SNR的增大,检测概率增大。可以明显看出,\alpha =0.4时,检测概率显著提高,但干扰效果差于\alpha =0.7、0.8、1.2、1.3。综合考虑覆盖范围和功率损失,常选用拉伸因子\alpha \in \left[ {0.6,0.9} \right]和\alpha \in \left[ {1.1,1.4} \right]的拉伸干扰。
3.3 拉伸干扰与噪声压制干扰对比
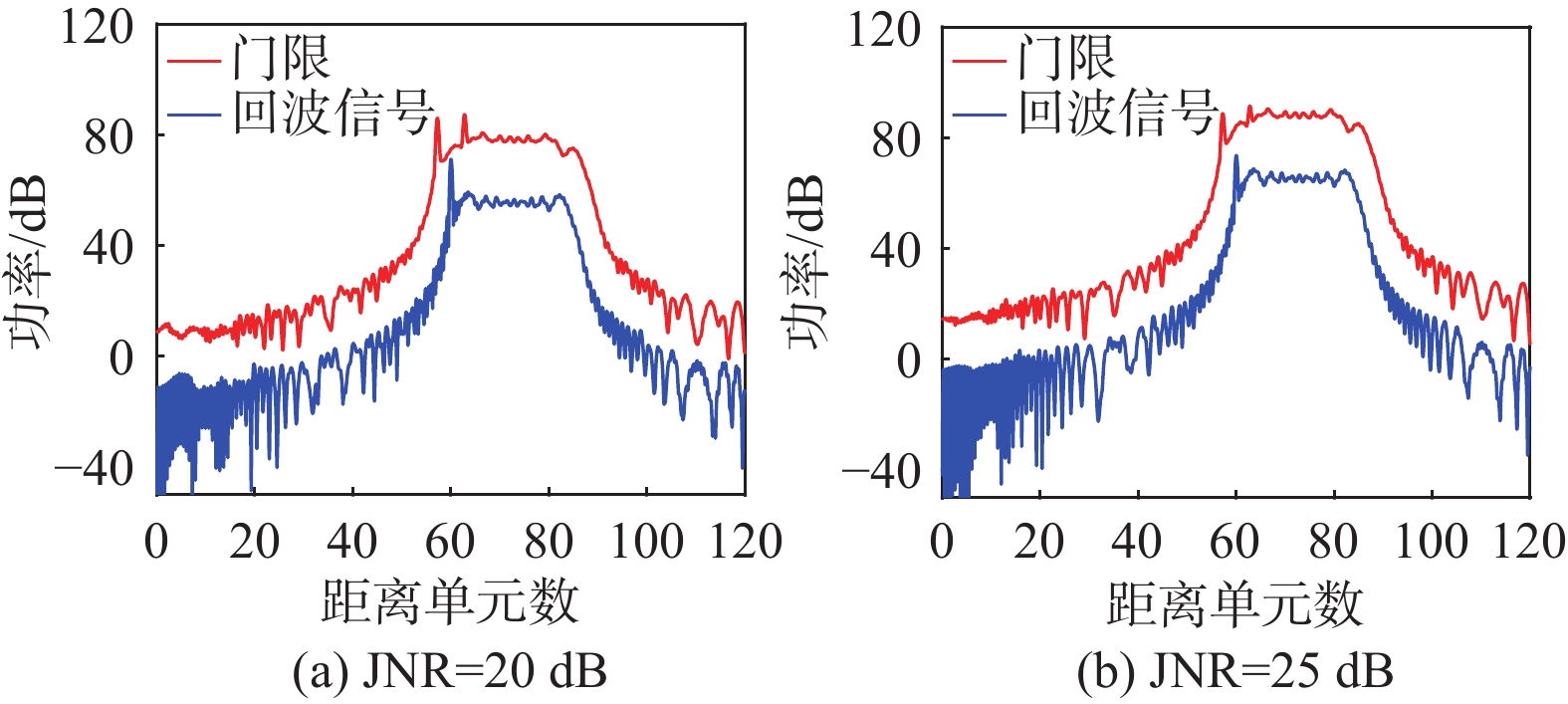
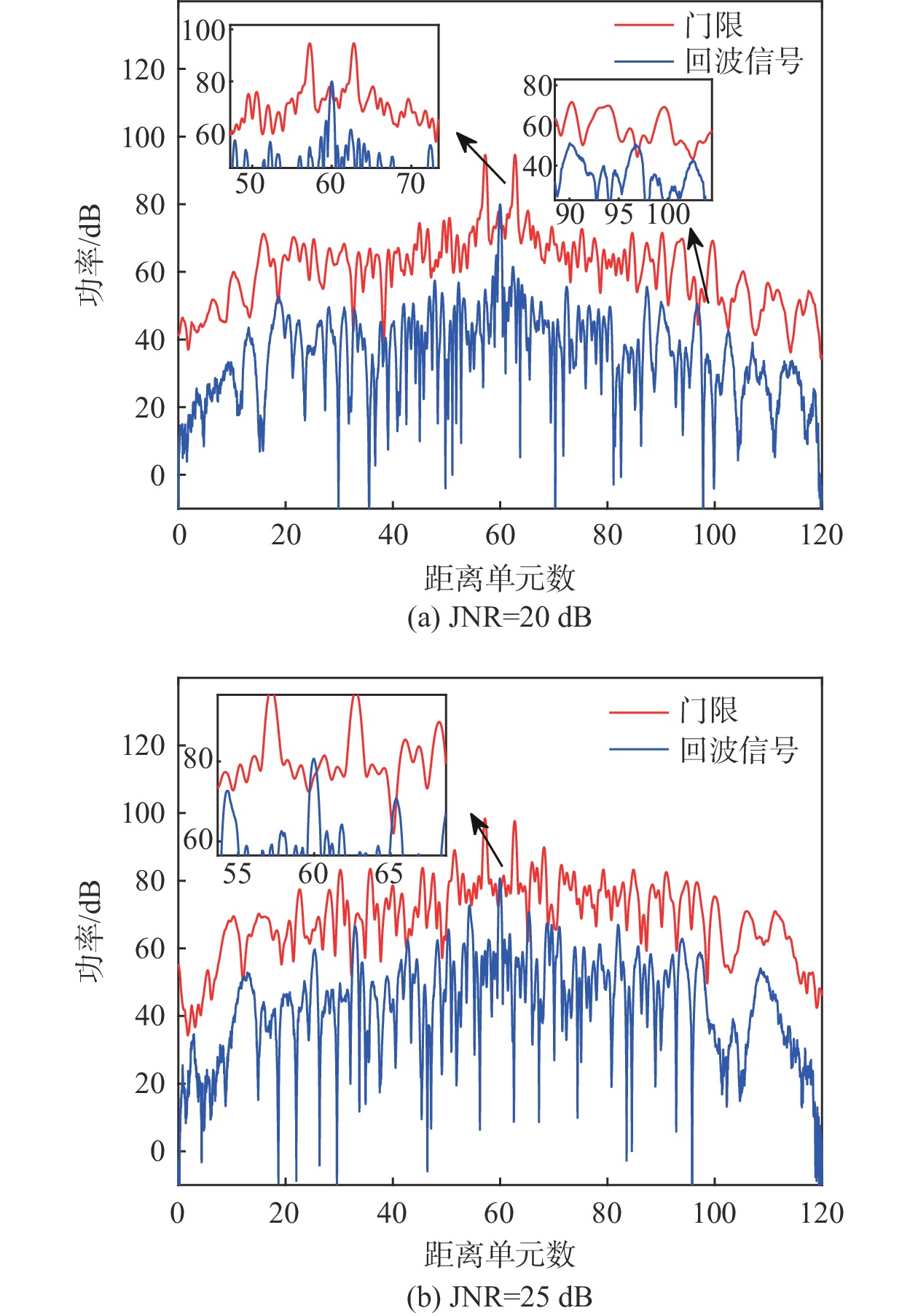
基于表2的参数设置,进行噪声压制干扰和拉伸干扰的仿真实验,取\alpha = 0.7,JNR=20、25 dB,拉伸干扰和噪声压制干扰对CA-CFAR检测的影响结果如图12~13所示。
由图12~13可以看出,拉伸干扰产生准等幅相对平坦的连片遮盖干扰,而噪声压制干扰使检测门限起伏大,杂乱无章。当拉伸干扰功率大于信号功率10 dB时,干扰对目标具有遮盖效果,而噪声压制干扰功率大于信号功率至少20 dB时才有压制效果,且拉伸干扰无需完全压制整个信号长度,只需抬高真实目标周围相邻多个检测窗长的幅值,就能抬升检测门限。因此,拉伸干扰对干扰机功率的需求大幅降低,能够灵活有效地控制遮盖目标。
本文得出的数值结论均以特定雷达参数为例,其他雷达具有相同变化规律,但数值结论需须进行具体研究。
4 结 论
本文提出了一种针对LFM雷达信号的拉伸变换干扰方法,并对脉压响应特性进行了研究,总结了拉伸干扰经脉压输出的泛主瓣区宽度、幅度变化趋势,得到了干扰效果可控的变化规律,并基于CA-CFAR检测方法对拉伸干扰进行了仿真验证。结果表明,拉伸干扰能够有效抬升CFAR检测电平,影响CFAR检测器检测目标。拉伸干扰能够形成准等幅大面积连片干扰效果;经过拉伸变换的“变换域信号”与“原始信号”进行互相关运算,是一类特殊的非匹配滤波处理;在工程上,拉伸干扰天然满足恒模约束,极大地提升了干扰机功率放大器的效率,同时,拉伸干扰的实现是基于DRFM数字域的一类基础运算−抽取、内插,易实现、运算量小、效率高,在工程上具有重要意义,为后续干扰信号的处理提供了更灵活高效的方式。
-
表 1 变化规律公式
Tab. 1 Formula for changing patterns
拉伸因子 泛主瓣区域
展宽宽度 {\tau _{\mathrm{J}}}覆盖距离单元数 \Delta {R_{\text{c}}} \alpha \in \left( {0,\infty } \right) \tau _{\mathrm{J}}^{{\mathrm{PW}}} = \dfrac{{\left| {1 - \alpha } \right|}}{\alpha }{T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{PW}}} = \dfrac{{\left| {1 - \alpha } \right|}}{\alpha }{T_{\text{p}}}{B_{\text{n}}} \alpha \in \left( {0,1} \right) \tau _{\mathrm{J}}^{{\mathrm{BW}}} = \left(1 - \alpha \right){T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{BW}}} = \left(1 - \alpha \right){T_{\text{p}}}{B_{\text{n}}} \alpha \in \left( {1,\infty } \right) \tau _{\mathrm{J}}^{{\mathrm{BW}}} = \dfrac{{\alpha - 1}}{\alpha }{T_{\text{p}}} \Delta R_{\text{c}}^{{\mathrm{BW}}} = \dfrac{{\alpha - 1}}{\alpha }{T_{\text{p}}}{B_{\text{n}}} 表 2 仿真参数设置
Tab. 2 Simulation parameter settings
参数 取值 雷达信号PW {T_{\text{p}}} 100\;{\text{μs}} 雷达信号BW {B_{\text{n}}} 1.2 MHz 采样率{f_{\text{s}}} 36 MHz 表 3 {\boldsymbol{\alpha \in \left( {0,1} \right)}}的干扰效果
Tab. 3 The jamming effect of stretching factor {\boldsymbol{\alpha}} \in \left( {{\boldsymbol{0}},{\boldsymbol{1}}} \right)
\alpha 干扰覆盖距离单元数/个 功率变化值/dB 0.9 13 -10.8 0.8 30 -13.8 0.6 80 -16.8 0.4 180 -18.6 表 4 {\boldsymbol{\alpha \in \left( {1,\infty } \right)}}的干扰效果
Tab. 4 The jamming effect of stretching factor {\boldsymbol{\alpha }}\in \left( {{\boldsymbol{1}},{\boldsymbol{\infty}} } \right)
\alpha 干扰覆盖距离单元数/个 功率变化值/dB 1.1 10 -10.8 1.2 20 -13.8 1.4 34 -16.8 1.6 45 -18.6 表 5 不同拉伸因子及SNR下的检测概率
Tab. 5 Detection probability under different stretching factors and SNR
SNR/ dB \alpha 0.7 0.8 1.2 1.3 0.4 −10 0.15 0.05 0.15 0.10 0.30 0 0.30 0.15 0.25 0.30 0.55 15 0.45 0.20 0.40 0.55 1.00 -
[1] MORRIS G V,KASTLE T A. Trends in electronic counter-countermeasures[C]//NTC’91-National Telesystems Conference Proceedings. Atlanta:IEEE,1991:265-269.
[2] LEWIS B L,KRETSCHMER F F. Linear frequency modulation derived polyphase pulse compression codes[J]. IEEE transactions on aerospace and electronic systems,1982,18(5):637-641.
[3] ZHU D K,LIU Y X,HUO K,et al. A novel high-precision phase-derived-range method for direct sampling LFM radar[J]. IEEE transactions on geoscience & remote sensing,2016,54(2):1131-1141.
[4] 王雪松,肖顺平,冯德军,等. 现代雷达电子战系统建模与仿真[M]. 北京:电子工业出版社,2010. WANG X S,XIAO S P,FENG D J,et al. Modeling and simulation of modern radar and electronic warfare systems[M]. Beijing:Publishing House of Electronics Industry,2010. (in Chinese)
[5] 刘忠. 基于DRFM的线性调频脉冲压缩雷达干扰新技术[D]. 长沙:国防科学技术大学,2006. LIU Z. Jamming technique for countering LFM pulse compression radar based on digital radio frequency memory[D]. Changsha:National University of Defense Technology,2006. (in Chinese)
[6] 张静克,代大海,邢世其,等. SAR脉内分段排序和脉间间歇采样复合转发干扰[J]. 电波科学学报,2015,30(2):224-231. doi: 10.13443/j.cjors.2014042802 ZHANG J K,DAI D H,XING S Q,et al. A composite repeating jamming method for SAR based on in-pulse separation and reordering and interpulse intermittent sampling[J]. Chinese journal of radio science,2015,30(2):224-231. (in Chinese) doi: 10.13443/j.cjors.2014042802
[7] 刘芳,陈嘉贝,吕欢,等. 新构型下多环路反向交叉眼干扰分析[J]. 电波科学学报,2020,35(4):603-613. doi: 10.13443/j.cjors.2020022003 LIU F,CHEN J B,LYU H,et al. Analysis of multi-loop reverse cross-eye jamming in new configuration[J]. Chinese journal of radio science,2020,35(4):603-613. (in Chinese) doi: 10.13443/j.cjors.2020022003
[8] 纪朋徽,邢世其,代大海,等. 基于逆chirp scaling的合成孔径雷达卷积欺骗干扰方法[J]. 电波科学学报,2023,38(6):1029-1039. doi: 10.12265/j.cjors.2022246 JI P H,XING S Q,DAI D H,et al. A SAR convolutional deceptive jamming method based on the inverse chirp scaling[J]. Chinese journal of radio science,2023,38(6):1029-1039. (in Chinese) doi: 10.12265/j.cjors.2022246
[9] 刘业民,刘忠,代大海,等. 散射波干扰对合成孔径雷达成像干扰效果的分析[J]. 电波科学学报,2011,26(2):400-407. LIU Y M,LIU Z,DAI D H,et al. Analysis of jamming effect on scatter wave jamming to SAR imaging[J]. Chinese journal of radio science,2011,26(2):400-407. (in Chinese)
[10] 王雪松,刘建成,张文明,等. 间歇采样转发干扰的数学原理[J]. 中国科学E辑:信息科学,2006,36(8):891-901. WANG X S,LIU J C,ZHANG W M,et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China series E:information sciences,2006,36(8):891-901. (in Chinese)
[11] 冯德军,陶华敏,杨勇,等. 对去斜体制雷达的间歇采样转发干扰[J]. 中国科学:信息科学,2012,42(2):186-195. doi: 10.1360/zf2012-42-2-186 FENG D J,TAO H M,YANG Y,et al. Jamming de-chirping radar using interrupted-sampling repeater[J]. Scientia sinica (informationis),2012,42(2):186-195. (in Chinese) doi: 10.1360/zf2012-42-2-186
[12] FENG D J,XU L T,PAN X Y,et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE transactions on aerospace and electronic systems,2017,53(3):1341-1354. doi: 10.1109/TAES.2017.2670958
[13] 徐乐涛. 基于间歇采样转发的宽带雷达相干扰研究[D]. 长沙:国防科学技术大学,2012. XU L T. Research on wideband radar coherent jamming based on intermittent-sampling repeater jamming[D]. Changsha:National University of Defense Technology,2012. (in Chinese)
[14] 黄洪旭,黄知涛,周一宇. 对合成孔径雷达的移频干扰研究[J]. 宇航学报,2006,27(3):463-468. doi: 10.3321/j.issn:1000-1328.2006.03.027 HUANG H X,HUANG Z T,ZHOU Y Y. A study on the shift-frequency jamming to SAR[J]. Journal of astronautics,2006,27(3):463-468. (in Chinese) doi: 10.3321/j.issn:1000-1328.2006.03.027
[15] 黄洪旭,黄知涛,周一宇. 对合成孔径雷达的随机移频干扰[J]. 信号处理,2007,23(1):41-45. doi: 10.3969/j.issn.1003-0530.2007.01.009 HUANG H X,HUANG Z T,ZHOU Y Y. Randomly-shift-frequency jamming style to SAR[J]. Journal of signal processing,2007,23(1):41-45. (in Chinese) doi: 10.3969/j.issn.1003-0530.2007.01.009
[16] 黄洪旭,黄知涛,吴京,等. 对合成孔径雷达的步进移频干扰[J]. 宇航学报,2011,32(4):898-902. HUANG H X,HUANG Z T,WU J,et al. Stepped-shift-frequency jamming to SAR[J]. Journal of astronautics,2011,32(4):898-902. (in Chinese)
[17] 周胜文,沙明辉,胡小春. 基于梳状谱调制和间歇采样重复转发的复合干扰[J]. 系统工程与电子技术,2021,43(12):3495-3501. doi: 10.12305/j.issn.1001-506X.2021.12.10 ZHOU S W,SHA M H,HU X C. Composite jamming based on comb spectrum modulation and interrupted sampling repetitive repeater[J]. Systems engineering and electronics,2021,43(12):3495-3501. (in Chinese) doi: 10.12305/j.issn.1001-506X.2021.12.10
[18] 刘一兵,罗强,刘记红,等. 基于分段移频调制的间歇采样重复转发干扰[J]. 电子信息对抗技术,2023,38(4):5-12. doi: 10.3969/j.issn.1674-2230.2023.04.002 LIU Y B,LUO Q,LIU J H,et al. Interrupted-sampling repetitive repeater jamming based on segmented shift-frequency modulation[J]. Electronic information warfare technology,2023,38(4):5-12. (in Chinese) doi: 10.3969/j.issn.1674-2230.2023.04.002
[19] 徐鹏,王振华,刘东青. 移频调制的非均匀重复转发干扰样式[J]. 现代防御技术,2019,47(3):113-120. XU P,WANG Z H,LIU D Q. Non-uniform repeated repeating jamming patterns based on shift frequency modulation[J]. Modern defence technology,2019,47(3):113-120. (in Chinese)
[20] 吴传章,陈伯孝. 间歇非均匀采样转发干扰产生方法研究[J]. 系统工程与电子技术,2021,43(1):1-10. doi: 10.3969/j.issn.1001-506X.2021.01.01 WU C Z,CHEN B X. Study on generating method of interrupted non-uniform sampling repeater jamming[J]. Systems engineering and electronics,2021,43(1):1-10. (in Chinese) doi: 10.3969/j.issn.1001-506X.2021.01.01
[21] 张家运,李文海,孙伟超,等. 一种LFM雷达间歇非均匀采样噪声调制转发干扰方法[J]. 舰船电子对抗,2023,46(1):28-32. ZHANG J Y,LI W H,SUN W C,et al. An intermittent non-uniform sampling repeater jamming method based on noise modulation to LFM radar[J]. Shipboard electronic countermeasure,2023,46(1):28-32. (in Chinese)
[22] 吴一戎,胡东辉. 一种新的合成孔径雷达压制干扰方法[J]. 电子与信息学报,2002,24(11):1664-1667. WU Y R,HU D H. A new noise jamming approach to SAR[J]. Journal of electronics & information technology,2002,24(11):1664-1667. (in Chinese)
[23] 周国富,毛二可. 频率调制对雷达线性调频脉冲压缩性能的影响[J]. 北京理工大学学报,2008,28(3):256-259. ZHOU G F,MAO E K. Effect of frequency modulation on the performance of pulse compression in radar linear frequency modulation[J]. Transactions of Beijing Institute of Technology,2008,28(3):256-259. (in Chinese)
[24] 薛成均,汤建龙,李昊,等. 调频斜率失配干扰与通信一体化研究[J]. 雷达科学与技术,2023,21(6):670-680+688. doi: 10.3969/j.issn.1672-2337.2023.06.011 XUE C J,TANG J L,LI H,et al. Study on the integration of FM slope mismatch jamming and communication[J]. Radar science and technology,2023,21(6):670-680+688. (in Chinese) doi: 10.3969/j.issn.1672-2337.2023.06.011
[25] 张煜,杨绍全,崔艳鹏. 对线性调频雷达的锯齿波加权调频干扰[J]. 西安电子科技大学学报,2007,34(2):209-212. ZHANG Y,YANG S Q,CUI Y P. Sawtooth weighted frequency modulated jamming technique for countering LFM radar[J]. Journal of Xidian University,2007,34(2):209-212. (in Chinese)
[26] 张煜,杨绍全,董春曦,等. 对线性调频雷达的正弦加权调频干扰技术[J]. 系统工程与电子技术,2007,29(4):544-547. doi: 10.3321/j.issn:1001-506X.2007.04.011 ZHANG Y,YANG S Q,DONG C X,et al. Sinusoidal weighted frequency modulation jamming technique countering LFM radar[J]. Systems engineering and electronics,2007,29(4):544-547. (in Chinese) doi: 10.3321/j.issn:1001-506X.2007.04.011
[27] 俞道滨,吴彦鸿,王宏艳,等. 对逆合成孔径雷达的多相位分段调制干扰方法研究[J]. 电子与信息学报,2017,39(2):423-429. YU D B,WU Y H,WANG H Y,et al. Research on multiple phase sectionalized modulation jamming method for inverse synthetic aperture radar[J]. Journal of electronics & information technology,2017,39(2):423-429. (in Chinese)
[28] 王宏艳,降佳伟,蒲娟,等. 基于余弦幅度加权的低旁瓣多相位分段调制干扰方法[J]. 系统工程与电子技术,2021,43(11):3185-3193. doi: 10.12305/j.issn.1001-506X.2021.11.18 WANG H Y,JIANG J W,PU J,et al. Multiple phases sectionalized modulation jamming method with low sidelobe based on cosine amplitude weighting[J]. Systems engineering and electronics,2021,43(11):3185-3193. (in Chinese) doi: 10.12305/j.issn.1001-506X.2021.11.18
[29] 降佳伟,吴彦鸿,王宏艳,等. 基于多相位分段调制的间歇采样转发干扰[J]. 系统工程与电子技术,2019,41(7):1450-1458. doi: 10.3969/j.issn.1001-506X.2019.07.03 JIANG J W,WU Y H,WANG H Y,et al. Intermittent sampling repeater jamming based on multiple phases sectionalized modulation[J]. Systems engineering and electronics,2019,41(7):1450-1458. (in Chinese) doi: 10.3969/j.issn.1001-506X.2019.07.03
[30] 降佳伟,王宏艳,吴彦鸿. 对地面动目标检测雷达的干扰技术综述[J]. 系统工程与电子技术,2020,42(11):2471-2480. doi: 10.3969/j.issn.1001-506X.2020.11.08 JIANG J W,WANG H Y,WU Y H. Review on jamming technology against ground moving target indication radar[J]. Systems engineering and electronics,2020,42(11):2471-2480. (in Chinese) doi: 10.3969/j.issn.1001-506X.2020.11.08
[31] 黄大通,邢世其,刘业民,等. 基于噪声卷积调制的SAR虚假信号生成新方法[J]. 雷达学报,2020,9(5):898-907. doi: 10.12000/JR20094 HUANG D T,XING S Q,LIU Y M,et al. Fake SAR signal generation method based on noise convolution modulation[J]. Journal of radars,2020,9(5):898-907. (in Chinese) doi: 10.12000/JR20094
[32] 黄大通,邢世其,李永祯,等. 基于乘积调制的SAR灵巧干扰方法[J]. 系统工程与电子技术,2021,43(11):3160-3168. doi: 10.12305/j.issn.1001-506X.2021.11.15 HUANG D T,XING S Q,LI Y Z,et al. Smart jamming method against SAR based on multiplication modulation[J]. Systems engineering and electronics,2021,43(11):3160-3168. (in Chinese) doi: 10.12305/j.issn.1001-506X.2021.11.15




 下载:
下载: