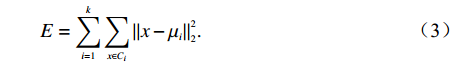RSSI ranging optimization algorithm based on BP neural network
-
摘要: 基于接收信号强度指示(received signal strength indication, RSSI)测距的研究和应用领域很广泛,一直是物联网研究的热点. 为降低传统基于反向传播(back propagation,BP)神经网络的RSSI测距误差,文中提出一种基于K-means聚类算法对样本数据进行预处理的BP神经网络测距算法,来解决由于RSSI值衰减程度不同引起的不同距离区间RSSI值和真实距离之间映射关系不均匀的问题. 将K-means聚类算法应用于BP神经网络模型中,对样本数据进行距离区间划分,然后将已经分类好的数据分别输入BP神经网络建立网络模型并进行实验仿真. 结果显示:传统基于BP神经网络的RSSI测距算法的均方根误差为1.425 7 m;而经过K-means算法改进后的BP神经网络测距算法的均方根误差为1.288 7 m,降低了测距误差,并优化了目标RSSI值与真实距离的映射关系.
-
关键词:
- 路径损耗模型 /
- 接收信号强度指示(RSSI)测距 /
- K-means聚类算法 /
- 反向传播(BP)神经网络 /
- 测距误差 /
- 均方根误差
Abstract: The research of ranging based on received signal strength indication (RSSI) has been a hot spot in the Internet of Things due to its wide application. In order to reduce the traditional RSSI ranging error based on back propagation neural network, a back propagation neural network RSSI ranging method based on K-means clustering algorithm preprocessing sample data is proposed. The algorithm solves the problem of non-uniform mapping between RSSI value and real distance in different distance intervals due to different attenuation degree of RSSI value. The K-means clustering algorithm is applied to BP neural network model to divide the distance interval of the sample data, and then the classified data are input into BP neural network to build the network model and simulate the experiment. The results show that the root mean square error of the traditional RSSI ranging method based on BP neural network is 1.4257 m, while the root mean square (RMS) error of BP ranging method neural network improved by K-means algorithm is 1.2887 m. Compared with the existing ranging methods based on BP neural network, it reduces the ranging error and optimizes the mapping relationship between the target RSSI and the real distance. -
引 言
基于接收信号强度指示(received signal strength indication, RSSI)测距的定位系统在日常生活多个领域有广泛应用,例如室内场所的定位服务,包括商品定位、地下停车场的车辆定位,以及提供消防救援和井下安全的人员定位等,无线定位技术成为当前研究的重点. 目前室外定位方面,GPS有实时、准确度高等特点,为人们的出行提供了很大便捷. 室内环境下[1]主要有WiFi、蓝牙、红外线以及射频识别(radio frequency identification, RFID)几种定位技术,由于卫星信号会被建筑物遮挡,如物流公司对快递投递的包裹等,许多情况下也不方便设置GPS模块. 这几种定位技术中,RFID技术由于成本低、精度高以及多目标识别等优点,被广泛应用在室内定位技术中[2].
基于RSSI测距结合三边定位法是目前最常用的一种RFID室内定位方法. 但由于信号的损耗系数以及在实际情况下信号衰弱难以计算等因素,RSSI测距的误差无法得到有效控制[3]. 文献[4]针对环境因素导致的测距误差较大问题提出了一种基于天牛须搜索的改进BP神经网络测距算法,克服了环境干扰,降低了误差. 文献[5]为了解决RSSI值的不稳定波动问题,提出一种结合中位数法和最短距离法来获取RSSI权值的方法,通过修正权值解决波动问题. 文献[6]针对RSSI测距误差较大的问题,提出了一种结合实时模型修正以及优化定位结果的方法. 文献[7]研究了人的存在和移动对不同距离处RSSI的影响. 文献[8]针对多元素影响RSSI测距准确性的问题,提出一种基于找到最佳节点方向的改进RSSI测距算法. 文献[9]针对RSSI距离映射的复杂度、稳定度以及定位精度问题,提出一种考虑分段传输模型和室内空间场景的优化方法. 文献[10]对传统RSSI测距算法进行分析并提出一种基于BP神经网络的测距算法,实验结果表明该算法提高了定位精度. 文献[11]针对动态室内环境中噪声、多径效应等问题对RSSI测距的影响,提出了一种基于斜率近似的改进RSSI测距算法. 文献[12]针对传统RSSI测距对环境参数过于依赖的问题,提出了一种基于蚁群算法优化BP神经网络的测距模型,提高了测距精度. 文献[13]提出一种融合加权质心以及自适应阈值选择的测距算法,提高了测距定位的精度和稳定性. 文献[14]为优化定位精度,提出一种采用高斯滤波方法并用粒子群算法对标签测距进行了优化. 上述研究者主要是在不同场景下对RSSI测距精度进行研究,提供了多个改进方向并使用了各种算法进行优化,但这些算法并未考虑到阅读器在识别标签时RSSI值与真实距离的映射关系会因为距离的变化而产生些许误差,其会引起测距精度不足进而影响定位系统的性能.
本文为减小这种测距误差,使用K-means聚类算法对采集的目标数据进行聚类,然后分别建立BP神经网络训练并测试,以降低将所有数据整体输入后导致的映射关系不均匀问题,并与改进前算法精度做分析对比.
1 RSSI测距
1.1 RSSI测距原理
由于实际室内环境具有静态和动态的障碍物,其会影响信号的正常传播,造成反射和折射等现象,进而导致阅读器接收到的信号强度不准确,存在误差. 经过大量实验发现,室内环境的信号传播距离与路径损耗服从以下分布模型[10]:
P(d)=P(d0)+10nlg(dd0)+X. (1) 式中:d是距离阅读器的真实距离,单位为m;P是对应距离下的信号接收强度;d0是参考距离;n是路径损耗常数,信号的损耗会随着距离的增加而增加,因此在不同的环境下,n的取值范围为1.5~4.5,并且在室内环境下最小;X为遮蔽因子,单位是dB,均值为0,均方差为4~10的正态随机变量[10]. 以下为简化后的模型:
RSSI = A−10nlg(d). (2) 式中,A是距离阅读器1 m处测到的信号强度,单位为dBm.
1.2 基于BP神经网络的测距方法
传统的RSSI测距算法对环境因素要求过高,直接利用该算法计算误差较大,应用局限性较高. 而具备非线性映射、自适应优点的BP神经网络,可以更好地处理环境因素等问题.
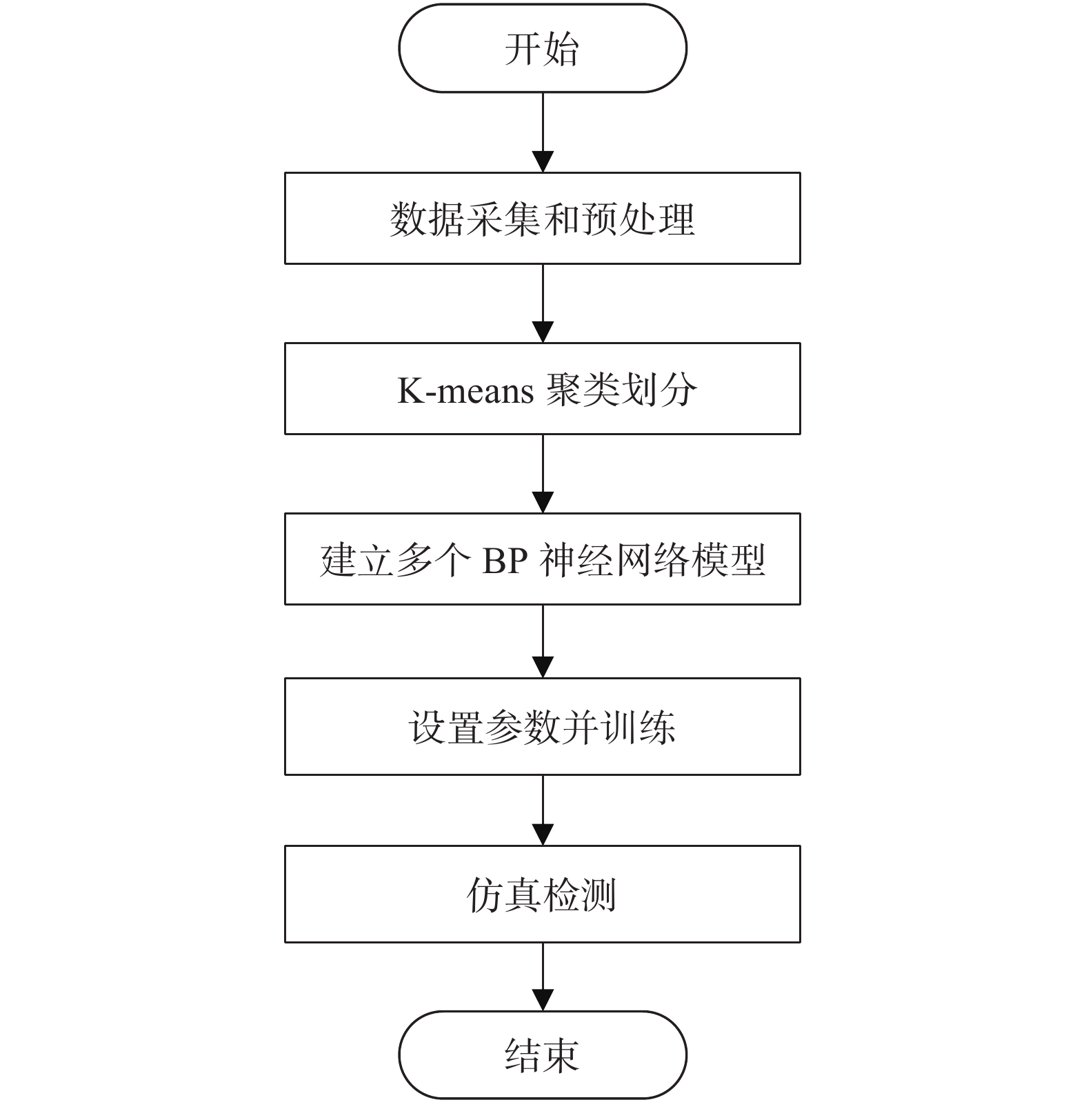
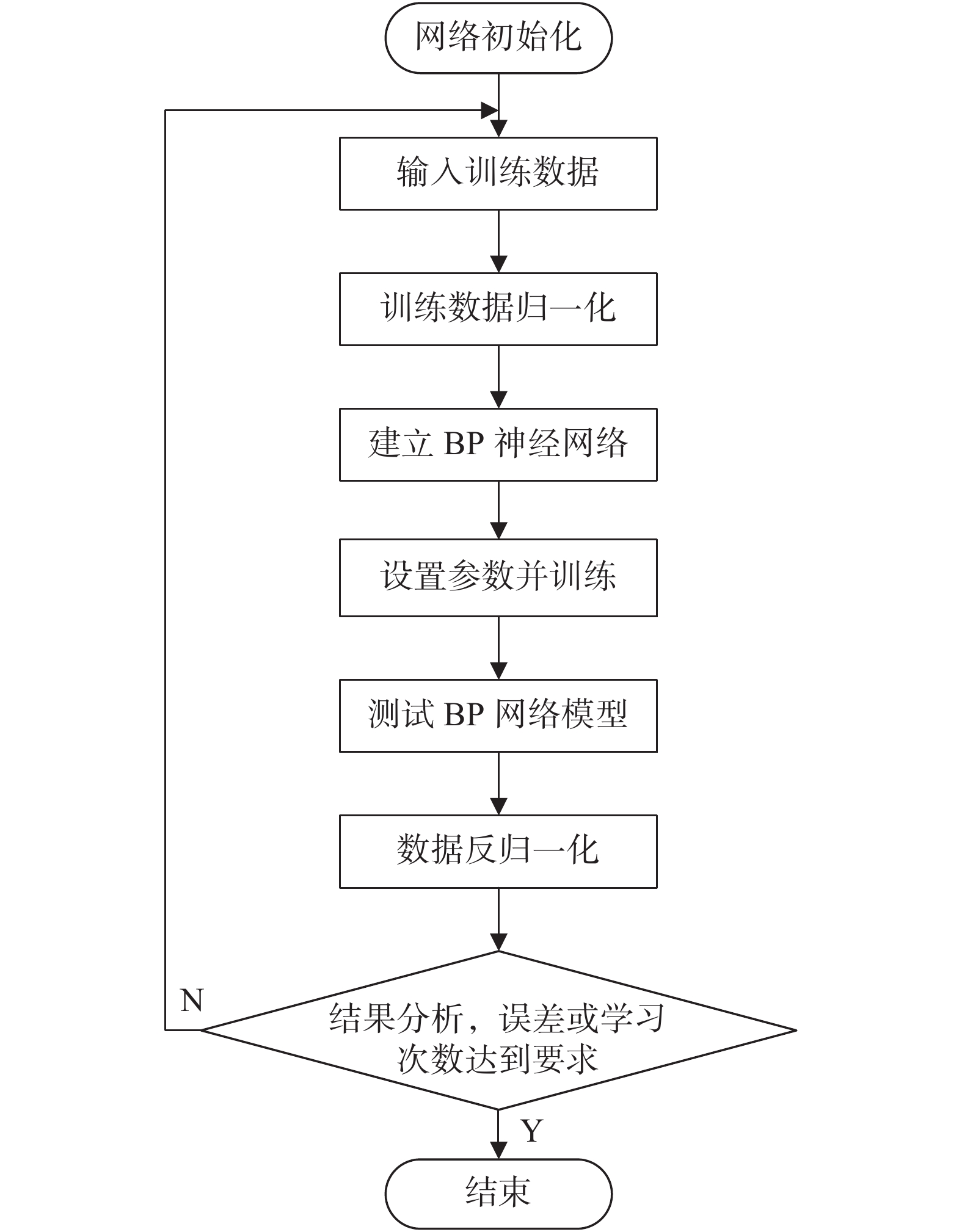
BP算法是一种基于人工神经网络的监督式机器学习算法,在各类应用中具有很好的非线性映射能力、自我学习和适应能力、泛化能力以及容错能力[15]. 在该算法下,先将输入数据作为训练数据,然后建立一个学习模型不断调整达到预期准确率,最后根据学习好的BP网络模型进行测试. 实现流程如图1所示.
文献[10]将采集的RSSI数据以及实际距离d建立训练数据库,以此构建了一个三层BP神经网络训练模型,采集的RSSI数据设定为输入数据,实际距离d设定为输出数据. 其中tansig和purelin函数分别设定为隐含层以及输出层的传递函数、trainlm为模型训练方式. 然后通过修改多次隐含层节点个数并测试,最终得出设定3个节点时测试效果最好. 最后将数据导入MATLAB中进行仿真测试,结果显示相对于传统RSSI测距算法而言,基于BP神经网络模型的RSSI测距误差更小,测距性能更好.
1.3 K-means聚类算法
上述基于BP神经网络改进的RSSI测距算法只是对构建网络进行优化,并未对采集数据的RSSI值和真实距离之间由于距离区间不同导致的映射关系不均匀问题进行处理. 本文使用聚类算法先对采集到的数据进行聚类处理,然后对多类数据分别建立BP神经网络模型,即可有效解决该问题.
K-means算法是一种基于计算点与点之间距离的聚类算法,具有简单、高效、快速收敛的优点. 计算两两目标之间的距离,距离越小越容易被分在一类,距离定义为欧式距离sqeuclidean、城市街区距离cityblock以及针对有时序关系数据的correlation等. 其算法思想是先在所有的样本数据中通过随机选取或自主设置的方式得到k个簇中心点,再把其他所有样本数据根据距离最近的原则划分到各个中心点所在的簇中,然后持续对簇中心点进行更新变化并且重新计算分类,当簇中心点不再变化即可确定一个最好的分类方式.
用模型表示,将k设置为需要划分的簇种类数量,各个类别分别为C1,C2,...,Ck,则算法的目的是最小化平方误差E.
E=k∑i=1∑x∈Ci‖ (3) 式中,μi是质心,
{\mu _i} = \frac{1}{{\left| {{C_i}} \right|}}\sum\limits_{x \in {C_i}} x . (4) 通过采用迭代方法,求出式(3)的最小值即可.
2 基于BP神经网络的改进测距算法
改进测距算法主要是根据RSSI值的不同衰减程度导致不同距离区间RSSI值与真实距离之间的映射关系不均匀问题. 首先通过K-means算法对训练数据进行区域分类,然后根据不同的分类区域建立多个网络模型进行分别训练,最后将需要测距的RSSI值对应所在距离区域的网络模型进行测距. 主要流程如图2所示.
2.1 数据采集和预处理
2.1.1 数据采集
为使建立的网络模型在训练时达到更好的效果,将之前基于BP神经网络测距算法的训练数据进行相同方式补充采集并作为下一步网络训练的输入数据,如表1所示.
表 1 补充后的训练数据Tab. 1 Supplementary training dataRSSI/dBm 距离/m RSSI/dBm 距离/m −24 1.0 −41 11.5 −25 1.5 −41 12.0 −25 2.0 −42 12.5 −26 2.5 −43 13.0 −27 3.0 −43 13.5 −27 3.5 −43 14.0 −29 4.0 −43 14.5 −30 4.5 −43 15.0 −31 5.0 −44 15.5 −33 5.5 −44 16.0 −33 6.0 −45 16.5 −33 6.5 −46 17.0 −35 7.0 −48 17.5 −36 7.5 −48 18.0 −36 8.0 −49 18.5 −37 8.5 −50 19.0 −38 9.0 −50 19.5 −38 9.5 −51 20.0 −39 10.0 −53 20.5 −40 10.5 −53 21.0 −40 11.0 2.1.2 归一化处理
对数据进行归一化处理后,分别找出RSSI数据及距离的最大、最小值,然后将这些值通过mapminmax函数规范到[0, 1]内,其作用是消除数据因为量纲不同对分析结果的影响,加快求出最优解速度的同时还可以提高测试精度.
2.2 划分距离区间
对输入数据预处理之后,采用K-means算法通过MATLAB软件将整理好的数据根据距离区间划分为若干个类. 本文以分两类为例进行算法研究. 算法主要分为六步,步骤如下:
1) 确定输入数据. 以RSSI值和与其对应的距离值建立坐标系,确定所有输入数据点Pi.
2) 确定分类个数K,然后随机选取K个点,作为K个类的聚类中心,用Kj表示.
3) 对所有数据点Pi进行遍历并计算其欧式距离,找到距每个数据点最近的中心点Kj,即第i个数据距离第j个中心点最近,Pi属于第j类.
4) 计算每个类的样本均值,更新其中心点.
5) 重复步骤3、4,直到聚类中心点不再变化.
6) 输出最终的聚类中心点以及j个类.
具体参数设置. 首先是聚类个数,本文旨在研究聚类后的拟合效果,为使BP神经网络达到更好的训练目标,聚类个数K设置为2,初始聚类中心根据所有数据的分布范围均匀生成,所以参数设置为uniform. 由于本文主要是为了研究真实环境下距离与RSSI之间的关系,而欧式距离这种定义方式能更好地反映两个点之间的真实距离,因此将距离参数设置为sqeuclidean.
2.3 BP神经网络训练
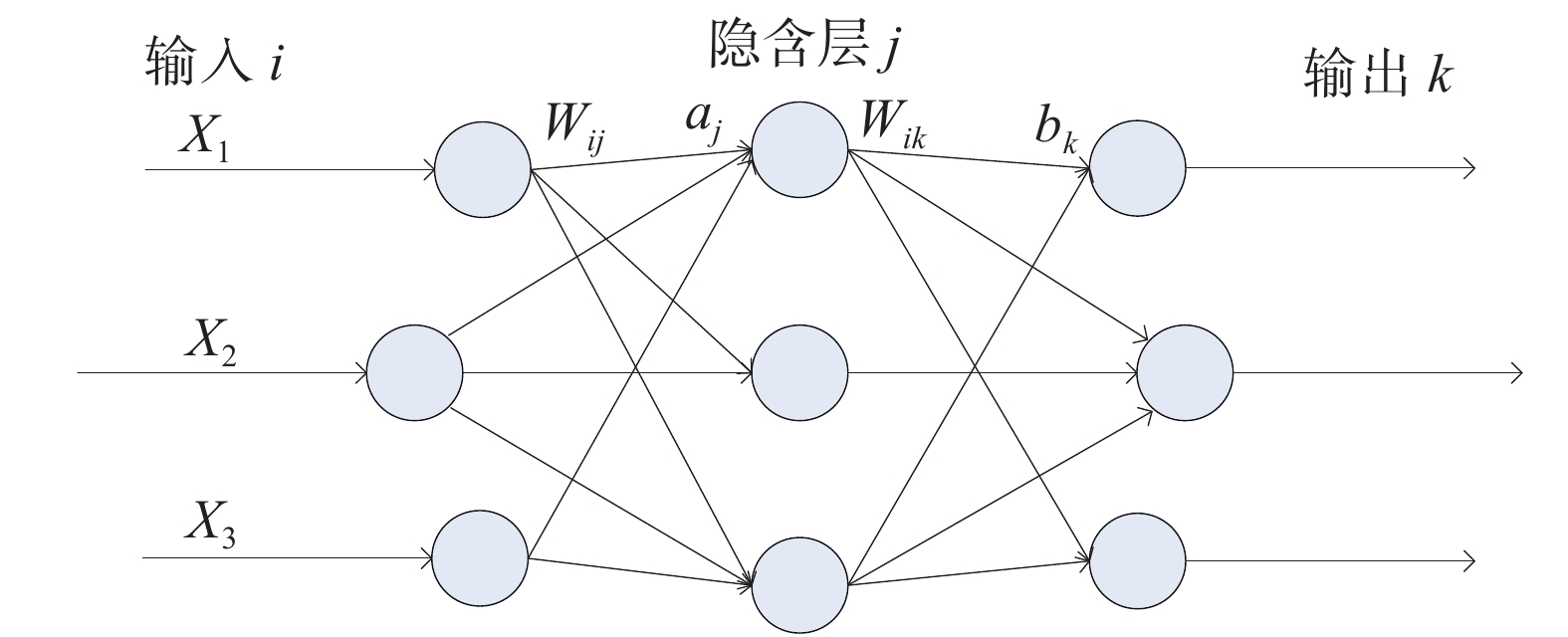
把输入数据通过K-means算法分成两类后,需要建立各自的BP神经网络学习模型,这里将归一化后的RSSI值作为输入数据,真实距离作为输出数据. 由于RSSI与距离d之间的关系可大致拟合为按对数衰减,模型不复杂. 经过多次实验发现,一直增加BP神经网络层数以及隐含层节点个数并不会降低误差,因此使用三层BP神经网络,并把隐含层节点设置为3个. 以训练集70%、验证集15%、测试集15%的样本分布对实验数据进行训练. 同样设置tansig和purelin函数为模型的隐层传递函数以及输出层传递函数. 对比trainlm、trainbr和trainscg三种算法,trainscg函数占用内存少,但训练结果误差较大(trainlm算法的误差仅为trainscg算法的55.1%). trainlm算法虽然占用比trainbr更多的内存,但训练时间快,且结果误差略小,因此本文设置trainlm函数作为BP神经网络的训练函数. 结构如图3所示.
3 实验仿真
3.1 实验仿真
3.1.1 输入数据处理和分类
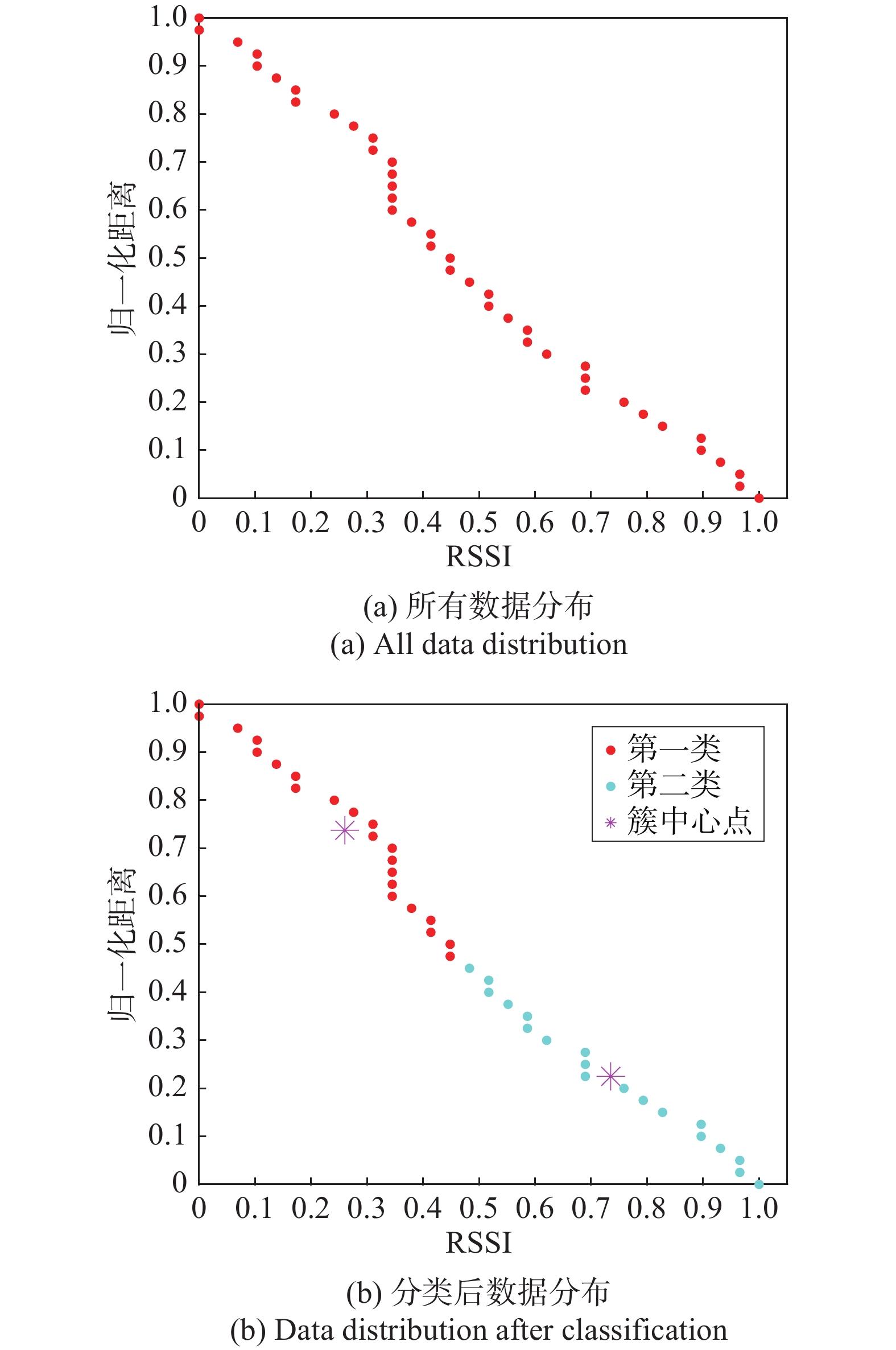
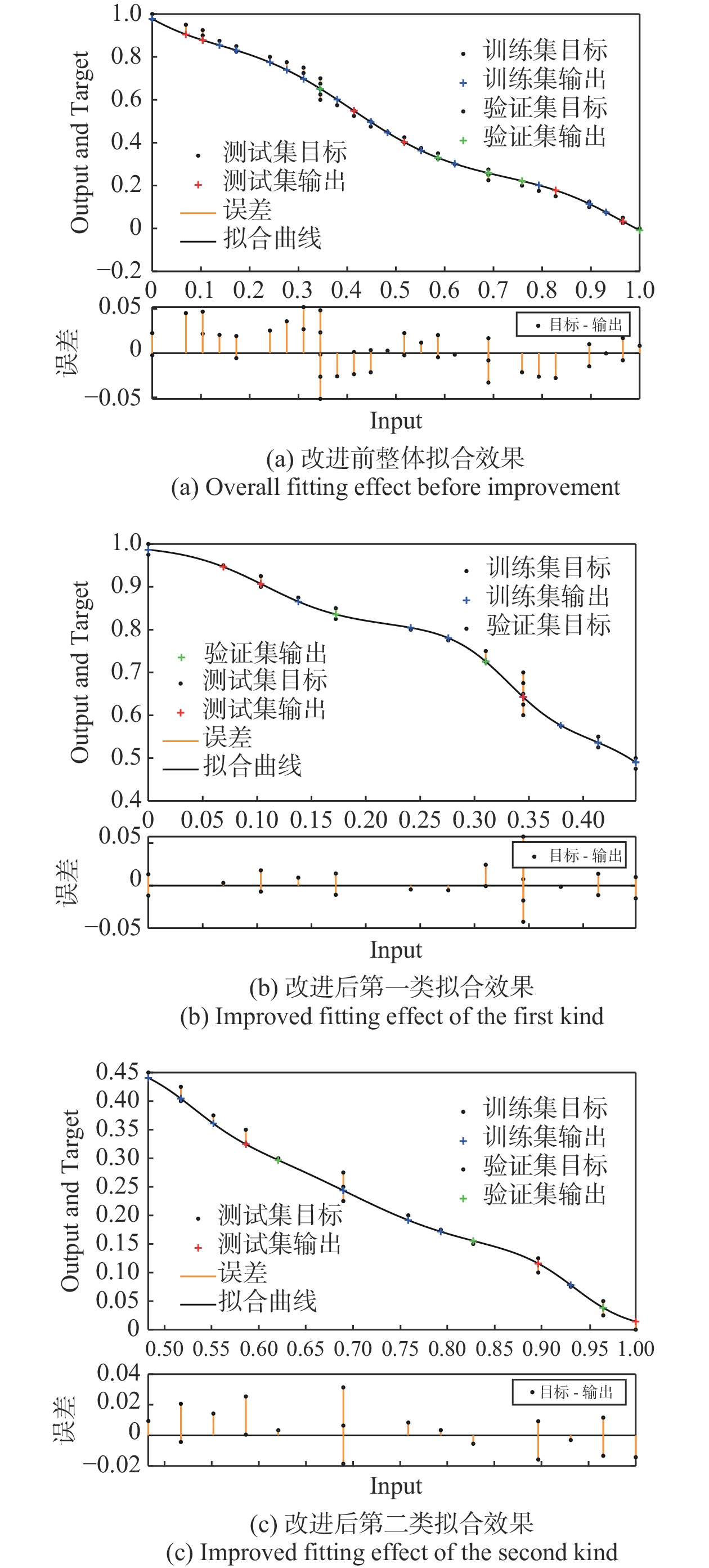
使用MATLAB仿真软件进行实验仿真,首先导入所要使用和处理的数据,经过mapminmax函数进行归一化处理后再通过K-means算法以及上述的参数选取对所有输入数据进行分类,将所有数据展示在坐标系上. 如图4所示,(a)是所有的数据分布,(b)是经过K-means分类后的结果以及两个类各自的簇中心点.
3.1.2 BP神经网络训练
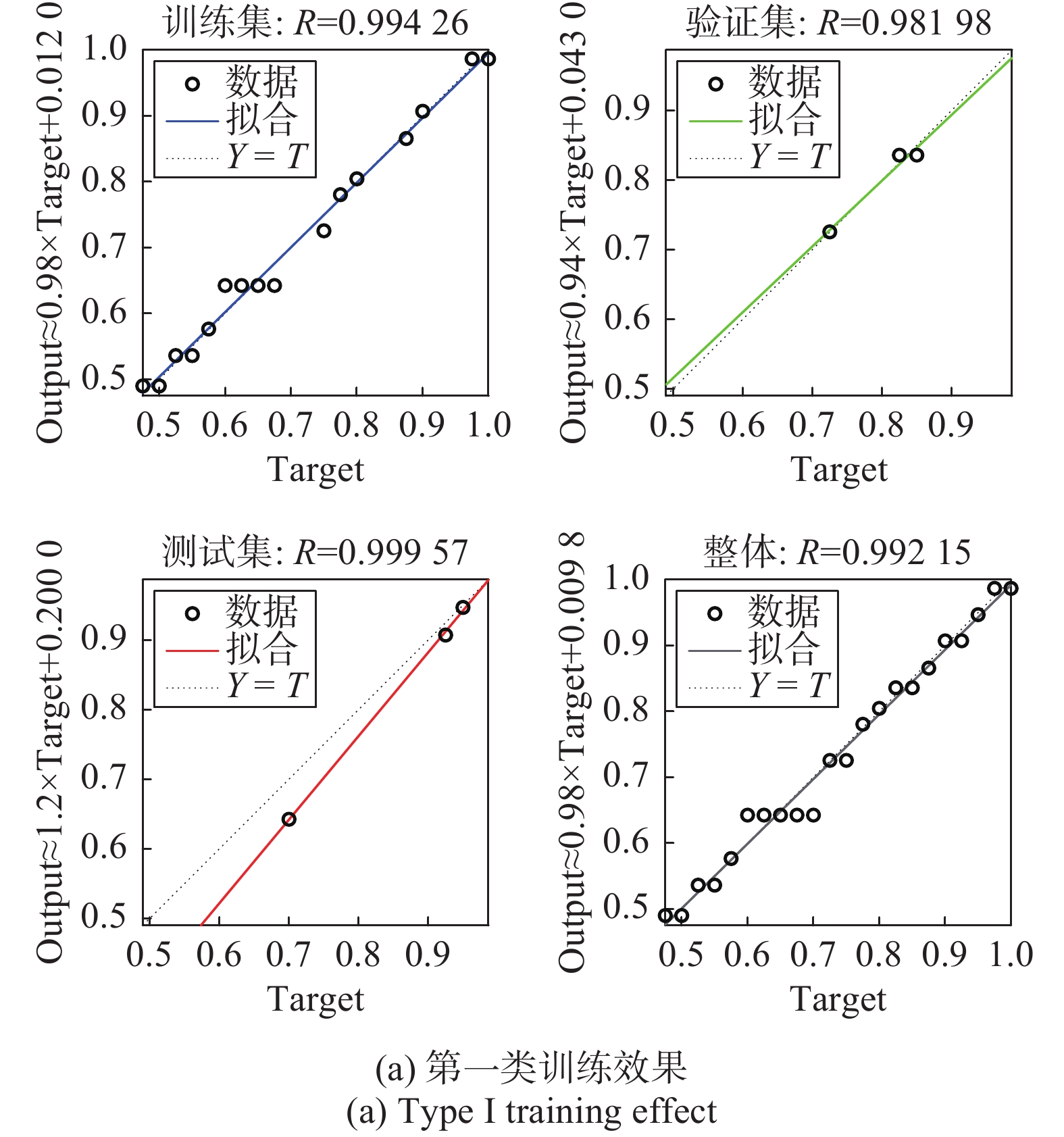
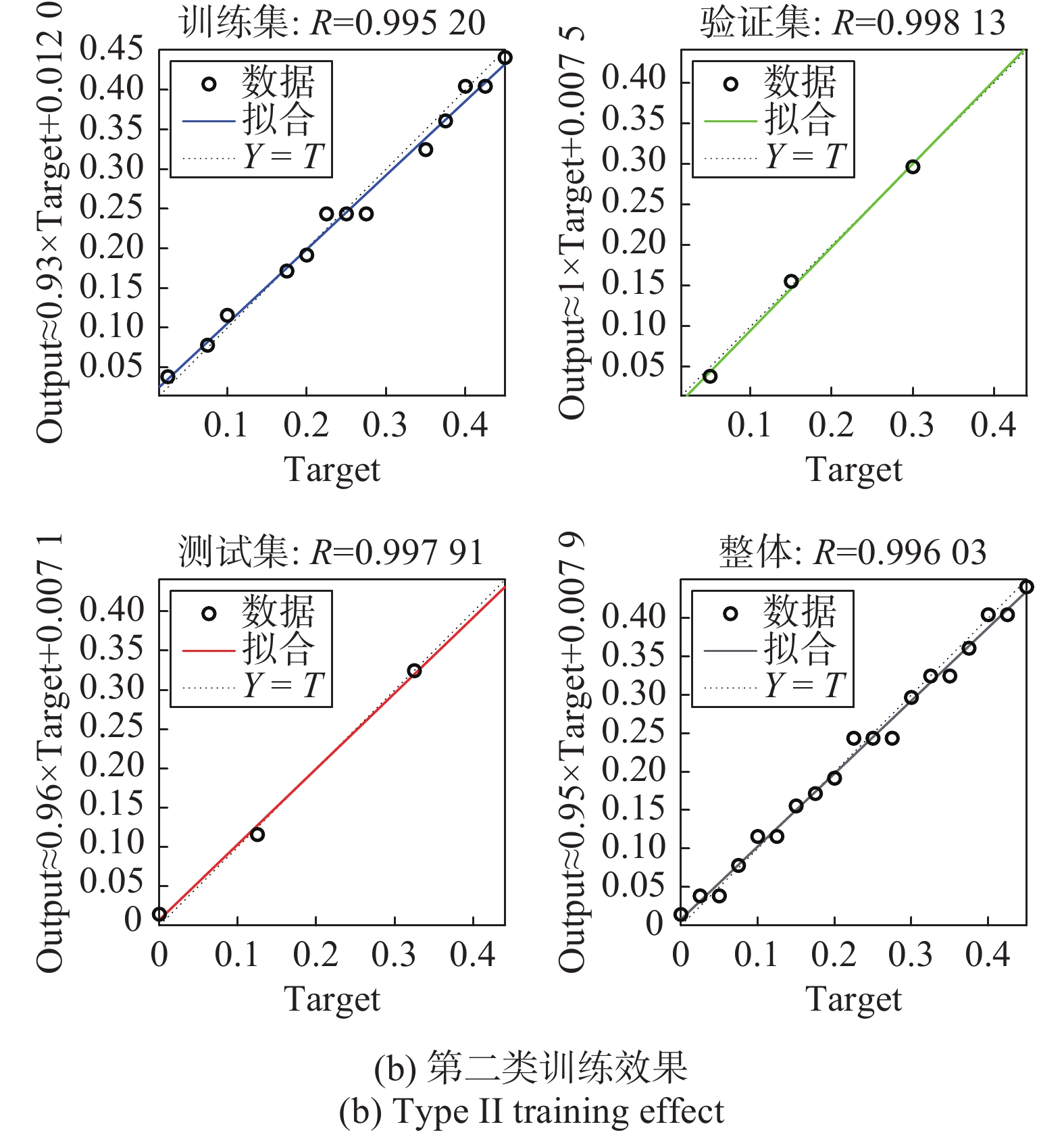
对两类数据分别进行BP神经网络训练,图5为训练效果. 可以看出,第一类的输出
{\rm{Output}} = 0.98 \times {\rm{Target}} + 0.009\;8 ,其中值为0.992;第二类{\rm{Output}} = 0.95 \times {\rm{Target}} + 0.007\;9 ,中值为0.996. 可见两个BP神经网络模型的拟合效果都比较理想,因此划分为两个类后建立的两个BP神经网络学习模型都是理想且可用的.3.2 对比算法分析
基于同样的数据,将RSSI值作为输入数据,距离d作为输出数据,使用三层BP神经网络,3个隐层节点,传递函数和样本分布皆与改进算法一致的方式进行仿真测试. 图6(a)是传统BP神经网络测距算法的拟合效果以及误差分布,(b)和(c)分别是改进算法第一类和第二类的拟合效果以及误差分布. 可以看出,本文改进算法的误差除个别因样本数据不均导致较大以外,普遍比传统BP神经网络算法要小.
对改进前后的算法以及一种信号加权算法进行误差分析,传统BP神经网络测距算法的均方根误差为1.425 7,信号加权算法的均方根误差为2.010 3,本文改进测距算法的均方根误差为1.288 7,综上可以看出本文的改进测距算法精度优于其他两种算法.
4 总 结
本文首先针对传统的信号传播路径损耗模型对基于RSSI的测距算法进行研究,提出先用K-means算法对数据进行预处理分类,再使用BP神经网络建立多个网络模型对RSSI进行分类测距. 该方法优化了由于不同距离区间的RSSI值衰减程度不均匀导致的误差问题. 根据MATLAB实验仿真的拟合效果以及误差分析结果可以看出优化后的BP神经网络测距算法对比传统BP测距算法拟合效果更好,误差更小.
-
表 1 补充后的训练数据
Tab. 1 Supplementary training data
RSSI/dBm 距离/m RSSI/dBm 距离/m −24 1.0 −41 11.5 −25 1.5 −41 12.0 −25 2.0 −42 12.5 −26 2.5 −43 13.0 −27 3.0 −43 13.5 −27 3.5 −43 14.0 −29 4.0 −43 14.5 −30 4.5 −43 15.0 −31 5.0 −44 15.5 −33 5.5 −44 16.0 −33 6.0 −45 16.5 −33 6.5 −46 17.0 −35 7.0 −48 17.5 −36 7.5 −48 18.0 −36 8.0 −49 18.5 −37 8.5 −50 19.0 −38 9.0 −50 19.5 −38 9.5 −51 20.0 −39 10.0 −53 20.5 −40 10.5 −53 21.0 −40 11.0 -
[1] 邓昀, 朱彦, 杨逸夫, 等. 基于BP神经网络的RFID室内定位算法研究[J]. 小型微型计算机系统,2019,40(8):1707-1712. doi: 10.3969/j.issn.1000-1220.2019.08.024 DENG Y, ZHU Y, YANG Y F, et al. Research on RFID indoor location algorithm based on BP neural network[J]. Journal of Chinese computer systems,2019,40(8):1707-1712. (in Chinese) doi: 10.3969/j.issn.1000-1220.2019.08.024
[2] WANG J, WANG Y, GUAN X. An indoor localization system based on backscatter RFID tag[C]// IEEE Wireless Communications and Networking Conference. IEEE, 2016: 1-6.
[3] 宋宁佳, 崔英花. 基于GA-GRNN的RFID室内定位算法[J]. 计算机工程,2019,45(11):298-302+308. SONG N J, CUI Y H. RFID indoor positioning algorithm based on GA-GRNN[J]. Computer engineering,2019,45(11):298-302+308. (in Chinese)
[4] 邹东尧, 陈鹏伟, 刘宽. 一种改进的RSSI测距定位算法[J]. 电讯技术,2019,59(10):1191-1196. doi: 10.3969/j.issn.1001-893x.2019.10.014 ZOU D Y, CHEN P W, LIU K. An improved RSSI ranging algorithm[J]. Telecommunication engineering,2019,59(10):1191-1196. (in Chinese) doi: 10.3969/j.issn.1001-893x.2019.10.014
[5] 谭志, 张卉. 无线传感器网络RSSI 定位算法的研究与改进[J]. 北京邮电大学学报,2013,36(3):88-91+107. TAN Z, ZHANG H. Research and improvement of RSSI localization algorithm in wireless sensor networks[J]. Journal of Beijing University of Posts and Telecommunications,2013,36(3):88-91+107. (in Chinese)
[6] 石琴琴, 徐强, 张建平, 等. 基于RSSI测距的室内目标定位方法[J]. 电子测量与仪器学报,2018,32(2):86-91. SHI Q Q, XU Q, ZHANG J P, et al. Indoor targeting method based on RSSI ranging[J]. Journal of electronic measurement and instrument,2018,32(2):86-91. (in Chinese)
[7] SASIWAT Y, JINDAPETCH N, BURANAPANICHKIT D, et al. An experimental study of human movement effects on RSSI levels in an indoor wireless network[C]//The 12th Biomedical Engineering International Conference (BMEiCON). IEEE, 2019: 1-5.
[8] IVANIĆ M, MEZEI I. Distance estimation based on rssi improvements of orientation aware nodes[C]// Zooming Innovation in Consumer Technologies Conference (ZINC). IEEE, 2018: 140-143.
[9] SHI Y, LONG Y, LU F, et al. Indoor RSSI trilateral algorithm considering piecewise and space-scene[C]// IEEE International Conference on Smart Cloud (SmartCloud), 2017: 278-282.
[10] 费扬, 杜庆治. 基于BP神经网络模型的RSSI测距方法研究[J]. 电波科学学报,2018,33(2):195-201. FEI Y, DU Q Z. RSSI ranging method based on BP neural network model[J]. Chinese journal of radio science,2018,33(2):195-201. (in Chinese)
[11] LI H, HUANG Z, SUN H, et al. A dynamic adaptive indoor ranging model based on RSSI[C]//The 39th Chinese Control Conference (CCC). IEEE, 2020: 2850-2855.
[12] 余振宝, 卢小平, 刘英, 等. 一种改进BP神经网络的接收信号强度测距算法[J]. 测绘科学, 2020, 45(11): 48-52+67. YU Z B, LU X P, LIU Y, et al. A ranging algorithm of received signal strength based on improved BP neural network [J]. Science of surveying and mapping, 2020, 45 (11): 48-52 + 67. (in Chinese)
[13] TANG J, HAN J. An improved received signal strength indicator positioning algorithm based on weighted centroid and adaptive threshold selection[J]. Alexandria engineering journal,2021,60(4):3915-3920. doi: 10.1016/j.aej.2021.02.031
[14] WANG C, WU F, SHI Z, et al. Indoor positioning technique by combining RFID and particle swarm optimization-based back propagation neural network[J]. Optik,2016,127(17):6839-684. doi: 10.1016/j.ijleo.2016.04.123
[15] 盖晴晴, 韩玉兵, 南华, 等. 基于深度卷积神经网络的极化雷达目标识别[J]. 电波科学学报,2018,33(5):575-582. GAI Q Q, HAN Y B, NAN H, et al. Polarimetric radar target recognition based on depth convolution neural network[J]. Chinese journal of radio science,2018,33(5):575-582. (in Chinese)
-
期刊类型引用(11)
1. 陈海英,李蕾. 大数据推导决策下多跳无线传感网络中继选择算法. 传感技术学报. 2025(05): 911-916 .  百度学术
百度学术
2. 李珂嘉,张璐薇,马跃洋,尹昱东,杨帆,张璐. 基于机器视觉的钢轨表面面型缺陷分类实验设计. 实验室研究与探索. 2024(03): 122-127+134 .  百度学术
百度学术
3. 韦进文,谭龙明,郭志俊,谭靖元,侯彦辰. 基于单天线视轴信号传播模型的RFID定位方法. 电子测量技术. 2024(06): 8-13 .  百度学术
百度学术
4. 高晨. 基于BP神经网络的睡眠质量监测管理系统设计. 吉林大学学报(信息科学版). 2024(03): 544-549 .  百度学术
百度学术
5. 林贻若,余科根,朱飞洋,布金伟. 一种基于GWO-BP神经网络的RSSI测距算法. 测绘学报. 2024(08): 1564-1573 .  百度学术
百度学术
6. 雷媛敬,王天慧,翟欣雨,王绍岩,刘海晨. 基于RSSI的医用蓝牙测距系统设计. 计算机与网络. 2024(05): 406-412 .  百度学术
百度学术
7. 钱志刚,杨东升,郭晓彤,李雪. 基于BP神经网络的对流层折射率预测方法研究. 全球定位系统. 2024(05): 120-125+132 .  百度学术
百度学术
8. Duo Peng,Mingshuo Liu,Kun Xie. Application of Adaptive Whale Optimization Algorithm Based BP Neural Network in RSSI Positioning. Journal of Beijing Institute of Technology. 2024(06): 516-529 .  必应学术
必应学术
9. 于明洁,夏斌,张立晔. 鸡群协同定位算法的研究. 无线电通信技术. 2023(03): 489-494 .  百度学术
百度学术
10. 管军,石爱业,徐传杰,李景奇,胡锐. 一种残差卷积与多尺度特征融合的海岛多时相遥感影像变化检测方法. 现代电子技术. 2023(14): 7-10 .  百度学术
百度学术
11. 陈思潼,朱锋,覃伊朵,杨晓滕. 神经网络优化5G定位结果域的分析与评估. 全球定位系统. 2022(06): 67-72 .  百度学术
百度学术
其他类型引用(17)




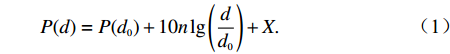

 下载:
下载: