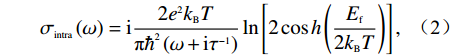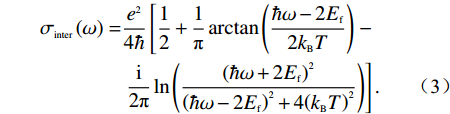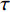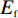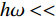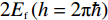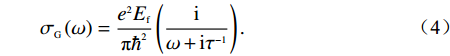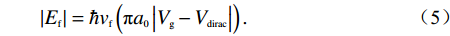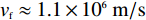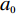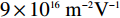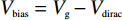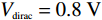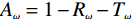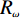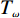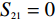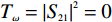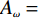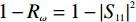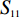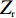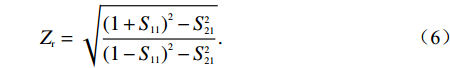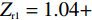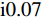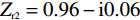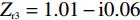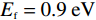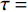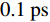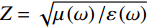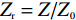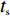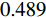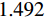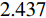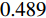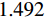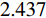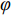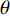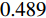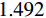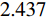Triple-band tunable terahertz perfect absorber based on graphene metamaterial
-
摘要: 为进一步降低太赫兹频率下高性能调控器件的结构复杂度,提出一种三频段可调谐超材料完美吸收器. 该吸收器由图案化的石墨烯层和经Si介质层隔开的Au接地平面组成,利用太赫兹下的石墨烯表面等离子体共振以及图案化石墨烯与电场耦合提供的电偶极子共振形成多个吸收峰. 数值仿真结果表明,在0.489 THz、1.492 THz和2.437 THz处实现了对入射波的共振吸收,各峰值处的幅值均大于99.9%. 由于吸收峰处的幅值可以通过外部施加的偏置电压改变石墨烯的费米能级进行控制,因而所提出的吸收器结构的工作状态可在反射器和吸收器之间灵活切换. 同时,通过对吸收器单元结构的对称设计实现了对极化角度的不敏感特性,且在宽入射角范围内仍能保持良好的吸收性能. 因此,所设计的基于石墨烯的太赫兹超材料功能器件在调制和传感方面具有巨大的潜力.Abstract: To further reduce the structural complexity of high-performance modulation devices in the terahertz region, we propose and demonstrate a triple-band tunable metamaterial perfect absorber, which consists of a patterned graphene and Au ground plane spaced by Si dielectric layer. The graphene surface plasmon resonance at the terahertz region is used to couple the patterned graphene with the electric field and provide electric dipole resonance to form multiple absorption peaks. Numerical results indicate that the amplitude of the absorption peaks is large than 99.9% at 0.489 THz, 1.492 THz, and 2.437 THz, respectively. In addition, due to the amplitude of the absorption peaks that can be controlled by the Fermi level via externally applied bias voltage, it means that we are able to switch the structure between reflector and absorber at their corresponding absorption bands. However, the symmetric unit cell structure of the proposed absorber is the inherent reason for the excellent polarization-insensitive, and the broadband absorption of the absorber maintains excellent absorption performance over a wide range of incident angles. Therefore, the designed graphene-based terahertz metamaterial function device has great potential in modulation and sensing.
-
Keywords:
- metamaterial /
- absorber /
- graphene /
- triple-band /
- tunable /
- polarization-insensitive
-
引 言
超材料作为一类人为设计的亚波长功能材料,具有负介电常数和负磁导率等特点。在过去的十年内,由于具备负折射率的左手行为,目前已在太赫兹功能器件的设计方面引起相当大的关注,并且具有广阔的应用前景[1-3]. 超材料完美吸收器能够在一定频率处或频率范围内实现对入射波的100%吸收,可灵活应用至通信领域. 尽管经典的超材料吸收器可以通过设计不同的几何形状来调整对入射波的吸收状态,但常因为吸收带宽窄,并且参数固定后吸收性能无法调整等原因造成大规模应用上的限制[4]. 近来,作为排列在蜂窝状晶格中的单层碳原子的二维材料石墨烯,基于其可调谐性、宽带响应、高载流子迁移率,已成为设计太赫兹超材料功能器件的最优选择[5-10]. 例如,张莹等人[8]选择将图案化的石墨烯与Au谐振器集成在一起,提出了一种极化不敏感的幅值可调宽带太赫兹吸收器结构;李九生等人[9]通过基于伞形石墨烯表面的经典三层结构设计出了三频段可调谐的太赫兹吸收器;王凤玲等人[10]利用两个不同尺寸的圆形石墨烯图案设计了一种可调谐且极化不敏感的双频太赫兹完美吸收器. 尽管基于石墨烯的太赫兹吸收器的研究已经取得了较大的进展,但是,如何在现有理论的基础上有效地降低结构的复杂度并设计出易制造、高效率、可调谐的太赫兹超材料完美吸收器仍是要面临的挑战.
在本文中,设计了一种三频段太赫兹超材料吸收器的三明治结构,它由相互耦合的图案化石墨烯层和经Si介质层隔开的Au反射平面组成. 数值仿真结果表明,该器件具有三频段、完美吸收、可调谐和极化不敏感等特性。并且,其相互耦合的图案化石墨烯层在实际应用中易于制造. 利用阻抗匹配理论对器件的吸收机制进行合理解释,并通过其电场和表面电流分布更加明确了完美吸收的内在机理. 因此,本文中所采用的灵活而简单的设计方法使得所提出的太赫兹超材料吸收器可应用于诸多领域,例如传感、检测和电光开关等.
1 结构设计
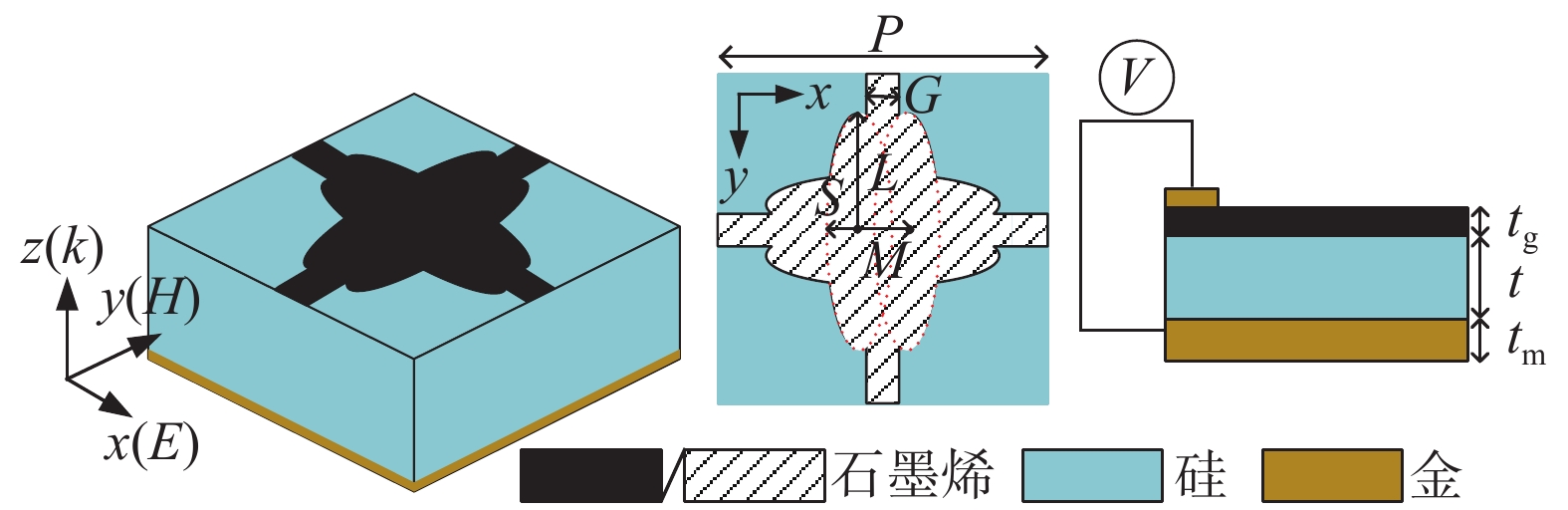
图1中展示了所设计的基于石墨烯的三频段可调谐太赫兹超材料吸收器的单元结构及具体参数. 从上至下共包含三层结构,顶层图案化石墨烯由四个相互重叠的椭圆形与交叉十字形相互耦合而成. 中间介质层采用无损耗的Si,其相对介电常数为
εd=11.9 [11],厚度设为t=45 μm. 而底面反射层则选用有损耗的金属Au,且其电导率设为σgold=4.561×107S/m [11],厚度tm=0.5 μm. 由于底层金属反射板的存在克服了趋肤效应,可完全阻止任何太赫兹波的透过,因此该吸收器的的透射率近似为0. 优化后的具体结构化参数如下:P=50μm, G=8μm,L=15μm,S=M=10μm .在仿真计算中,石墨烯的表面电导率可利用著名的Kubo公式进行描述,其表面电导率包括了带内和带间电导率贡献[12-15]:
σG(ω)=σinter(ω)+σintra(ω). (1) σintra(ω)=i2e2kBTπℏ2(ω+iτ−1)ln[2cosh(Ef2kBT)], (2) σinter(ω)=e24ℏ[12+1πarctan(ℏω−2Ef2kBT)−i2πln((ℏω+2Ef)2(ℏω−2Ef)2+4(kBT)2)]. (3) 式中:
ω 是入射波的角频率;kB,e,ℏ 分别代表玻尔兹曼常数、电子电荷以及约化普朗克常数;T为环境的绝对温度;τ 为弛豫时间;Ef 是石墨烯的费米能级. 事实上,当太赫兹波段内的光子能量hω<< 2Ef(h=2πℏ) 时,根据Pauli排斥原理,石墨烯的表面电导率主要取决于带内电导率的贡献值. 因此可将石墨烯表面电导率的公式简化为Drude模型进行描述[16-17],即σG(ω)=e2Efπℏ2(iω+iτ−1). (4) 另外,石墨烯的表面电导率具有连续可调的光学特性. 通过石墨烯层与衬底构成的平行板电容器结构,费米能级与偏置电压呈线性关系. 因此可以通过施加外部偏置电压来改变其费米能级. 如图1中所示,可通过在结构顶层放置的金属电极与底层金属板间施加的偏置电压来改变石墨烯的费米能级,进一步达到调节其表面电导率的目的. 其中,石墨烯的费米能级
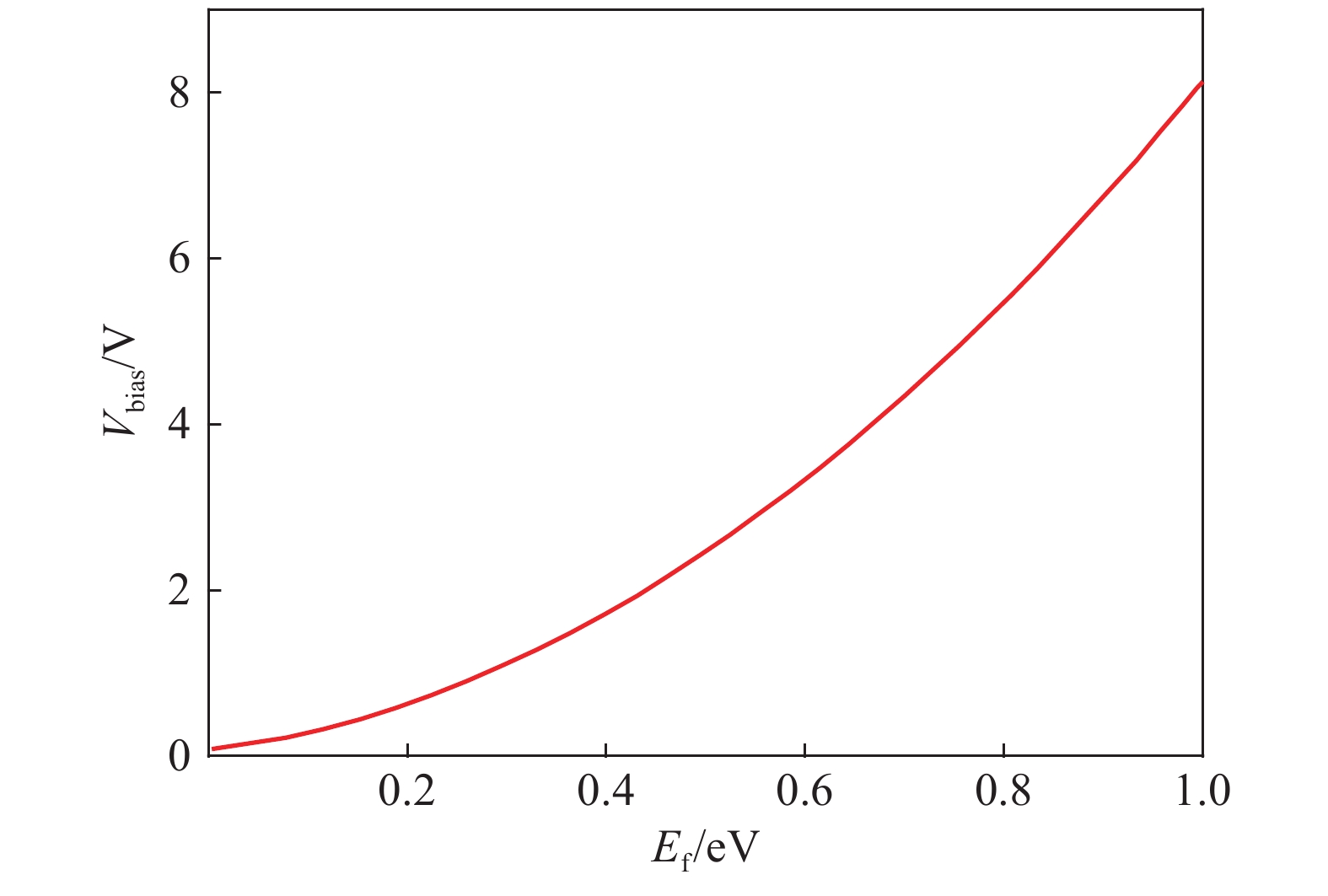
Ef 与偏置电压Vbias 的关系如图2所示. 显然,随着费米能级的不断增加,所需的偏置电压也越来越大. 其相关计算公式可定义为[8,18]|Ef|=ℏvf(πa0|Vg−Vdirac|). (5) 式中:费米速度
vf≈1.1×106m/s [8,18];a0 的估算值为9×1016m−2V−1 ;Vbias=Vg−Vdirac ,自然掺杂所引起的狄拉克电压偏移Vdirac=0.8V . 通过商用软件CST Microwave Studio的频域有限元法(finite element method, FEM)求解器获得数值仿真结果[6]. 在x轴和y轴方向上采用周期性单元边界条件(unit cell),z轴方向上采用开放性边界条件,即入射波垂直于器件表面,并通过局部网格细化和自适应网格细化来提高数值仿真的精度. 此外,吸收器的吸收率Aω=1−Rω−Tω ,其中Rω 和Tω 分别表示结构的反射率和传输率. 注意到,由于地面金属板的存在,阻止了任何太赫兹波透过结构,因此,可认为其透射系数S21=0 ,进而可以得到吸收器的传输率Tω=|S21|2=0 . 因此,所提出的三频段太赫兹超材料完美吸收器的吸收率Aω= 1−Rω=1−|S11|2 [17],其中,S11 表示结构的反射系数.2 关键参数对吸收性能的影响分析
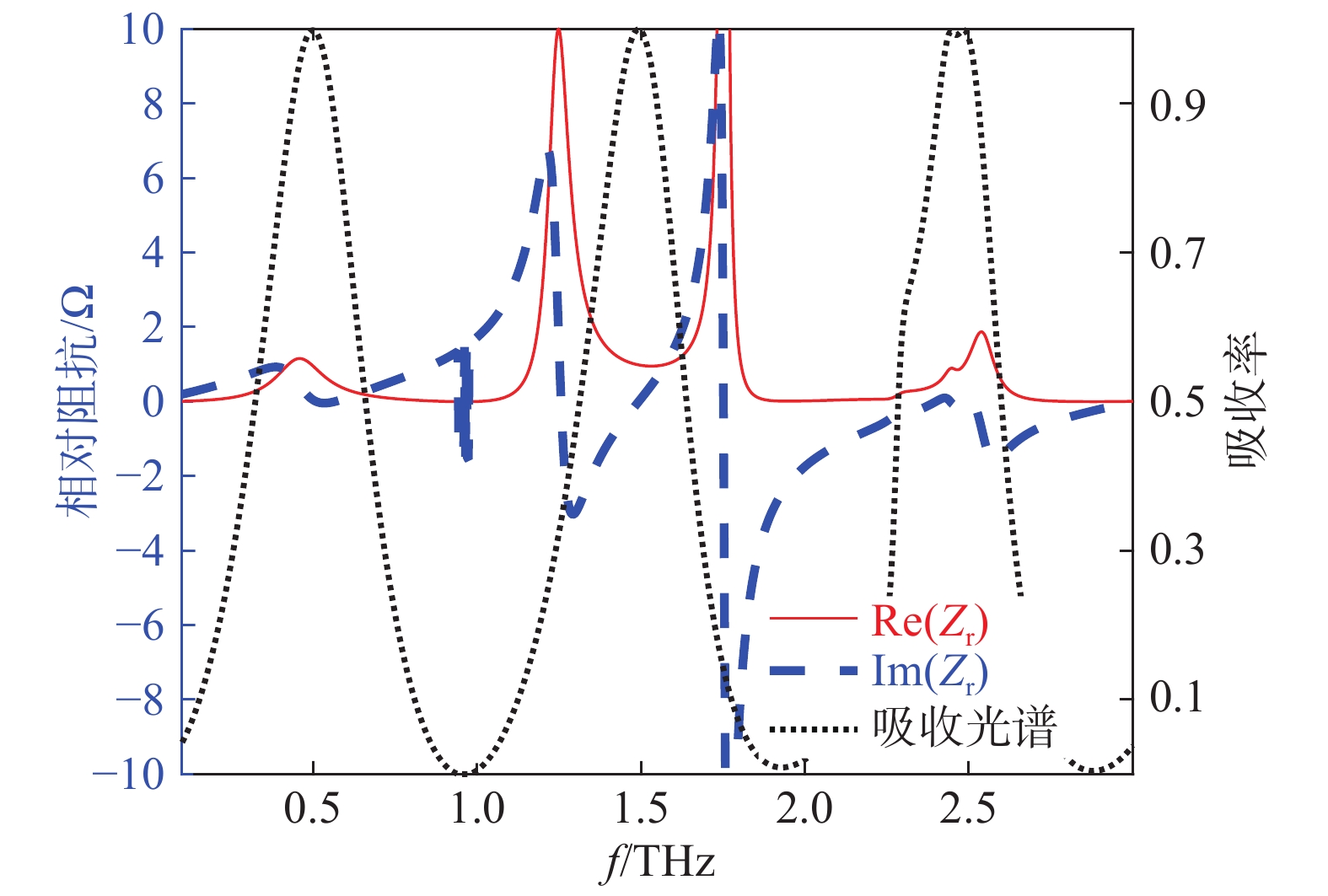
为进一步研究所提出的完美吸收器的内在机理,根据阻抗匹配理论,当吸收器的等效阻抗与自由空间阻抗匹配时,反射系数会最小化,通过调整结构参数可以获得最佳匹配. 如图3所示,为进行结构参数优化后的太赫兹三频段吸收光谱及其相对阻抗的实部和虚部. 数值仿真结果表明,当器件处于横向磁(transverse magnetic, TM)极化模式时,在0.489 THz、1.492 THz和2.437 THz处,吸收峰的振幅值分别达到了99.9%,99.9%和99.9%,实现了完美吸收效果. 在此过程中,吸收器结构的相对阻抗
Zr 可以定义为[19]Zr=√(1+S11)2−S221(1−S11)2−S221. (6) 如图3中所示,根据式 (6) 可计算得到吸收器在各共振频率处的相对阻抗分别为
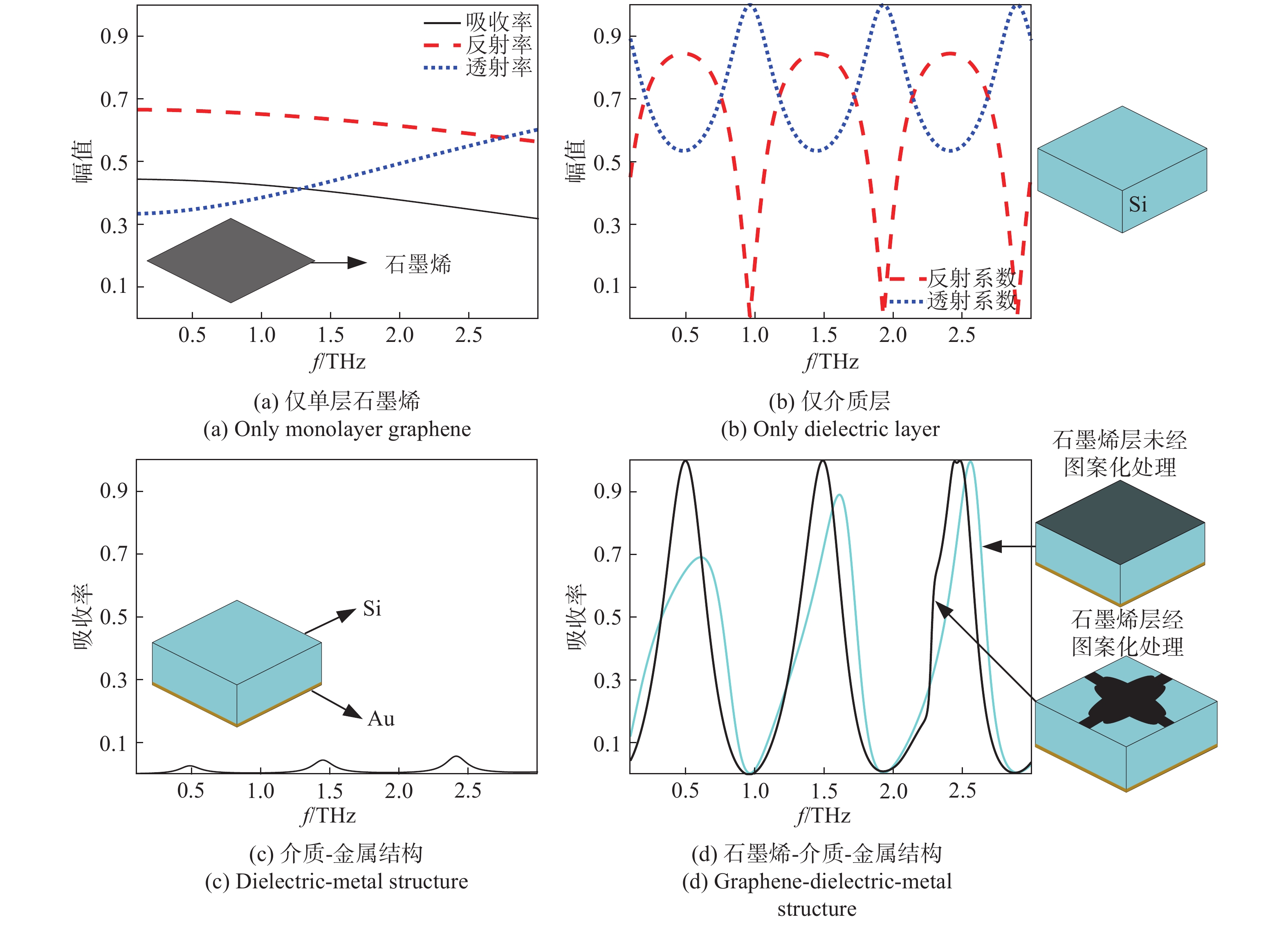
Zr1=1.04+ i0.07 、Zr2=0.96−i0.06 以及Zr3=1.01−i0.06 . 显然,在完美吸收峰处,吸收器结构有效阻抗的实部接近于1而虚部近似为0,与自由空间的有效阻抗 (Z0=377 Ω)匹配良好. 意味着吸收器在以上三个共振频率处都能够完全吸收入射的太赫兹波,达到了最佳的完美吸收状态.当太赫兹波垂直于器件表面入射时,自由空间中单层石墨烯材料的吸收曲线如图4(a)所示. 先前的研究表明,自由空间中单层吸波材料对电磁波的吸收率最高为50%[20] ,并且,未经图案化处理的石墨烯材料对入射波的吸收效果将随着频率的增加而逐渐减小. 为了更好地解决这一问题,本文提出了一种石墨烯-介质-金属的经典三层吸收器结构. 其中底部金属作为反射层,将结构的透射率降至最低而最大化地实现对波的吸收. 如图4(b)中所示,利用仿真软件分别模拟了Si介质的反射谱和透射谱. 显然,在0.481 THz、1.481 THz和2.481 THz处分别存在三个不同的反射峰,其频率间隔为 ∆f =1 THz.当金属反射层被添加到结构底部时,如图4(c)中所示,仍然具有三个吸收率较低且极为相似的吸收峰,即分别在0.486 THz、1.449 THz和2.414 THz处获得了约 2.5%、3.7%和5.6%的吸收幅值. 事实上,这种现象的产生可由Fabry-Perot共振模型进行解释,相邻谐振峰之间的频率间隔可以描述为 ∆f=c/ 2n t d cos φ . 其中, φ 表示电磁波的入射角, c 为光速, n 和 t d 分别表示Si介质的有效折射率和厚度。当入射波垂直于Si介质表面入射时,其所产生的共振频率间隔刚好为∆ f =1 THz,这与仿真计算所得到的结果一致。另外,相比于未经图案化处理的石墨烯层而言,图案化石墨烯的引入改变了吸收器结构的有效阻抗,使其与自由空间更加匹配,增强了结构整体的吸收性能,分别在0.489 THz、1.492 THz和2.437 THz处实现了完美吸收效果.
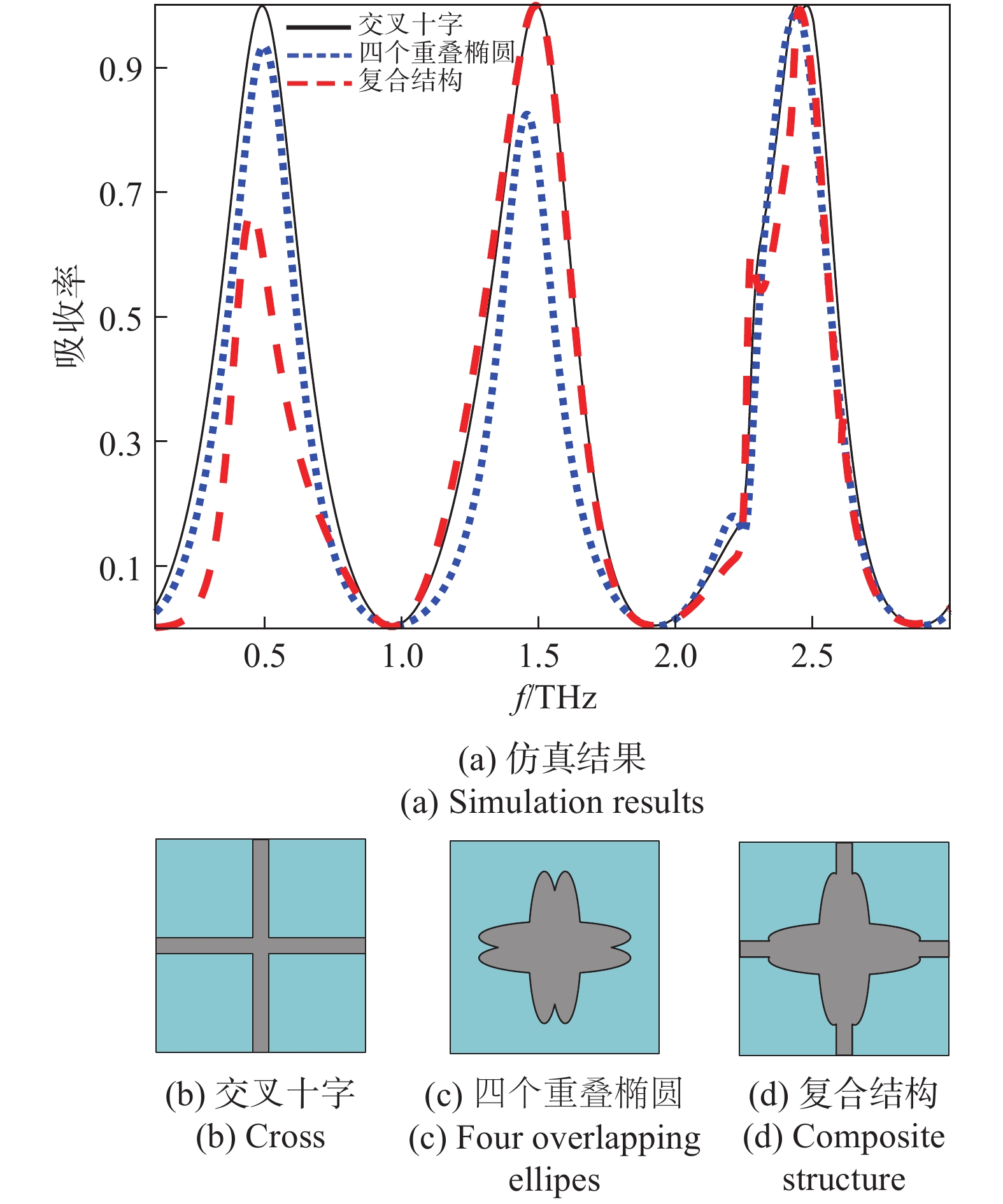
当石墨烯的费米能级和弛豫时间分别设置为
Ef=0.9eV 和τ= 0.1ps 时,在图5中单独研究了垂直入射下组成耦合图案化石墨烯结构各部分的吸收光谱. 各部分结构分别包括了复合图案化石墨烯中基于十字交叉形,具有四个重叠的椭圆形以及基于十字交叉和四个重叠椭圆的复合形状. 从图5(a)可以看出,当吸收器中的石墨烯层由单独的十字交叉结构组成时,在0.494 THz、1.457 THz和2.443 THz处分别存在三个明显的吸收峰,吸收率分别为0.935、0.826和0.988,如图中黑线所示. 随后,当吸收器的石墨烯层由单独的四个重叠的椭形结构构成时,则在0.450 THz、1.490 THz和2.452 THz处分别存在三个相似的吸收峰,对应的吸收率分别达到了0.669、0.999和0.994,如图中蓝线所示。而当石墨烯层由交叉十字形与四个重叠的椭圆结构耦合而成时,将分别在0.489 THz、1.492 THz和2.437 THz处产生三个完美吸收峰,对应的吸收率分别可达0.999、0.999和0.999,如图中红线所示. 因此,结构间的耦合效应可有效提升器件的吸收性能。意味着可利用两个单独的结构之间的耦合效应来实现太赫兹功能器件的的良好性能[6, 21].介质层的损耗角正切以及厚度的改变对吸收性能的影响如图6所示. 从图6 (a)可以看出,介质层损耗角正切的改变对吸收性能影响非常小,这意味着完美吸收发生的主要原因是结构参数的改变,而非介质的损耗. 从图6 (b)可知,器件的吸收效率对介质的厚度的改变非常敏感. 具体而言,随着介质层厚度从41 μm增加至47 μm,三频吸收带在保持红移的同时其峰值吸收率均出现了先增大后减小的情况. 这种现象可由阻抗匹配理论具体解释,由于结构的有效阻抗和相对阻抗可分别由公式
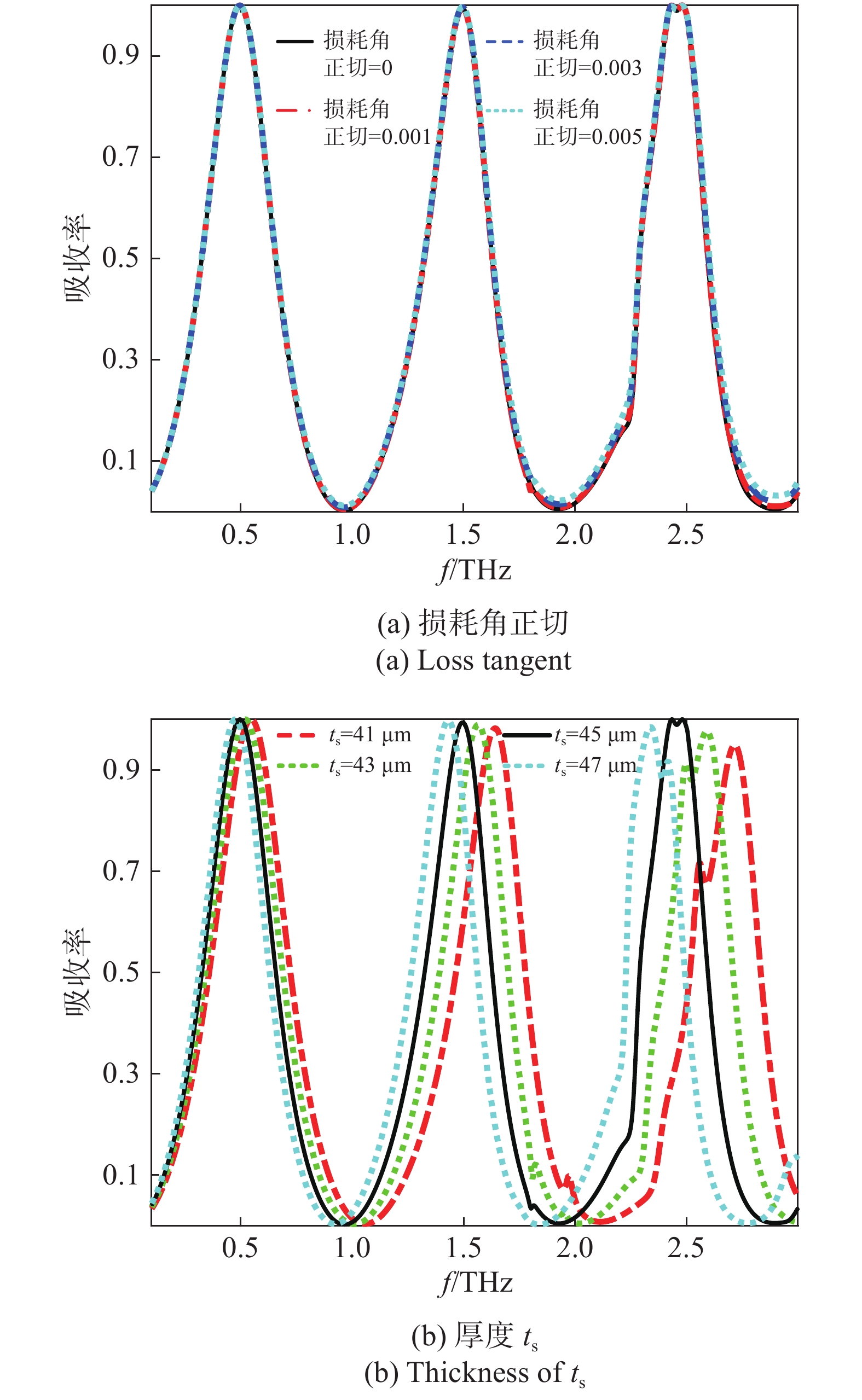
Z=√μ(ω)/ε(ω) ,Zr=Z/Z0 表示. 当介质层的厚度发生改变时,顶层石墨烯阵列与底层金属间的不同耦合效应导致磁导率μ(ω) 发生变化,将导致吸收器与自由空间之间的相对阻抗发生改变. 当厚度ts 从41 μm增加至45 μm 时,结构的有效阻抗将与自由空间的阻抗逐渐匹配;而当ts 大于45 μm时,良好的阻抗匹配被破坏,从而产生不同的吸收光谱. 因此,所提出的吸收器结构的厚度最终优化为45 μm.另外,对于参数固定的吸收器结构而言,幅值可调谐性在实际中具有重要的应用价值. 具体而言,可通过调节施加在石墨烯上的偏置电压来调整石墨烯的费米能级实现其幅值可调. 图7 (a)给出了吸收器结构在不同费米能级下的吸收光谱. 显然,随着石墨烯费米能级的不断增加,三个共振频率处的吸收率均逐渐接近100%. 换言之,当费米能级设置为0 eV时,可认为此时吸收器处于“关闭”状态(反射率>72 %). 相反,当费米能级设置为0.9 eV时,在相应谐振吸收频率处的吸收幅值均超过90 %,即吸收器处于“打开”状态(吸收率>90 %). 所以,当石墨烯的费米能级从0 eV逐渐变化至0.9 eV时,结构的工作状态可在反射与吸收之间自由切换[22]. 另外,从图7 (b) 吸收器结构在不同弛豫时间的吸收光谱中可以看出,随着石墨烯弛豫时间从0.1 ps增加至0.5 ps,结构的吸收率逐渐下降,并且中心频率出现蓝移. 这是由于石墨烯弛豫时间增加导致石墨烯载流子浓度降低,使得良好的阻抗匹配被破坏. 因此,将石墨烯的弛豫时间优化为0.1 ps.
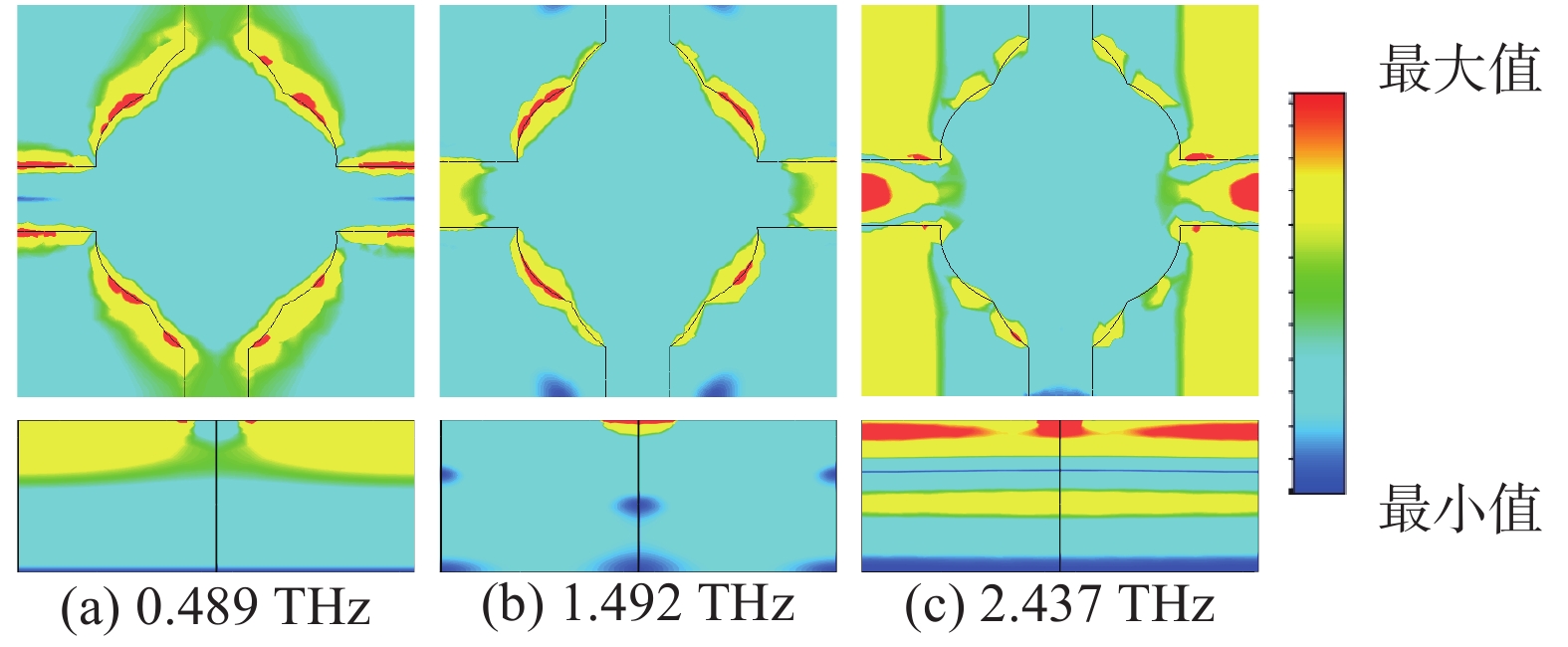
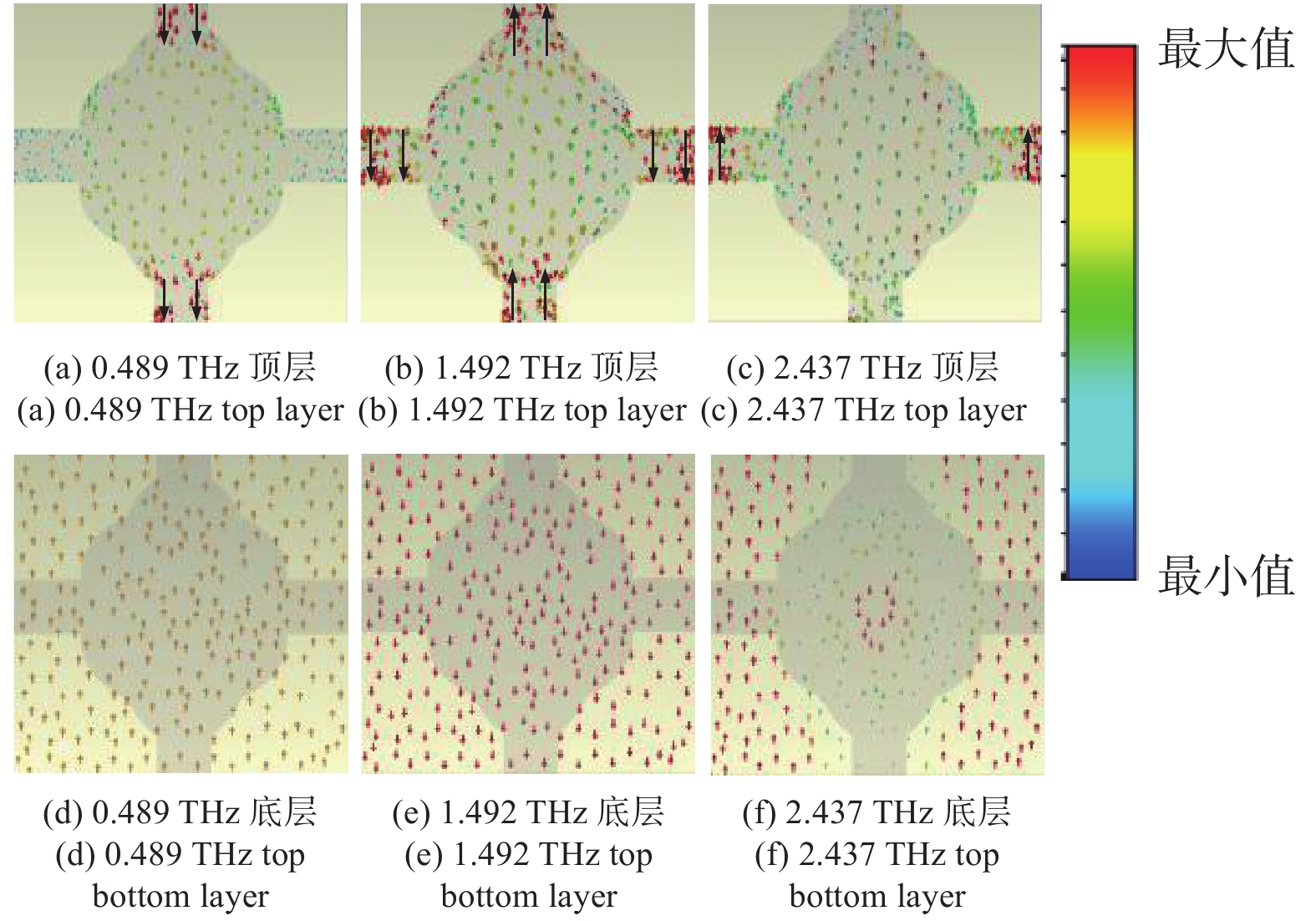
为进一步了解上述完美吸收器的内在物理机制,分别监测
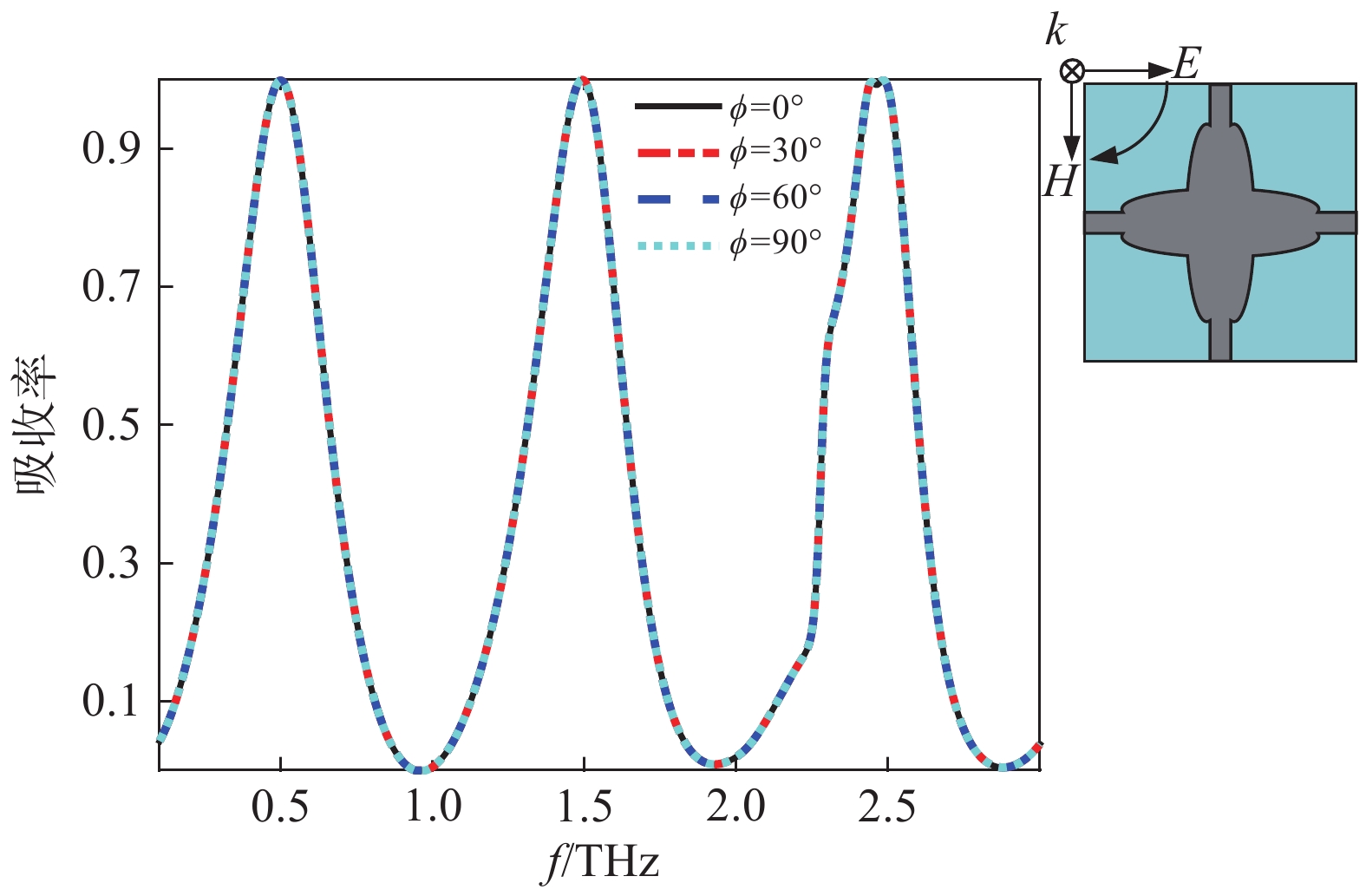
0.489 THz、1.492 THz和2.437 THz三个共振频率处结构的电场分布情况,结果如图8所示. 显然,通过对电场分布的侧视图所表现出的特征分析可知,在0.489 THz和1.492 THz处,石墨烯在太赫兹波段的表面等离子体共振使得图案化的石墨烯与电场相互耦合,并提供了电偶极子共振. 如图8 (a)和8 (b)所示,表面电荷沿着由外部电场驱动的图案化石墨烯超表面的侧围震荡. 另一方面,在2.437 THz处,其电场分布的侧视图所表现出的特征呈现典型的高阶模式[9],如图8 (c)所示. 此时电场主要分布在十字交叉臂上,但在石墨烯结构的两侧均有较强的电场分布,这是顶层石墨烯和底层金属反射层之间产生的强磁共振导致的. 此外,在图9中分别描绘了共振频率处的顶层石墨烯阵列和底层金属板上的表面电流分布情况. 事实上,入射太赫兹波的磁分量在顶层石墨烯阵列和底层金属板之间来回传递,并在顶层石墨烯阵列和底层金属板上产生反向平行的表面电流,从而导致耦合磁共振. 综合分析图8和图9可以看出,吸收器所产生的三个吸收峰主要来自顶层石墨烯超表面阵列的电偶极子共振以及顶层和底层之间存在的磁共振.在实际应用中,超材料吸收器的极化不敏感的特性对诸多领域具备潜在吸引力. 当石墨烯的费米能级设为0.9 eV时,不同极化角度下的吸收光谱如图10所示,显然,不同极化角下的吸收曲线保持高度一致. 事实上,所设计的超材料吸收器的极化不敏感特性主要归因于单元结构的对称性. 因此,当太赫兹波垂直入射时,以上结果表明该太赫兹超材料功能器件可在不同的极化模式下保持吸收效率的同步,提升了其实际应用价值.
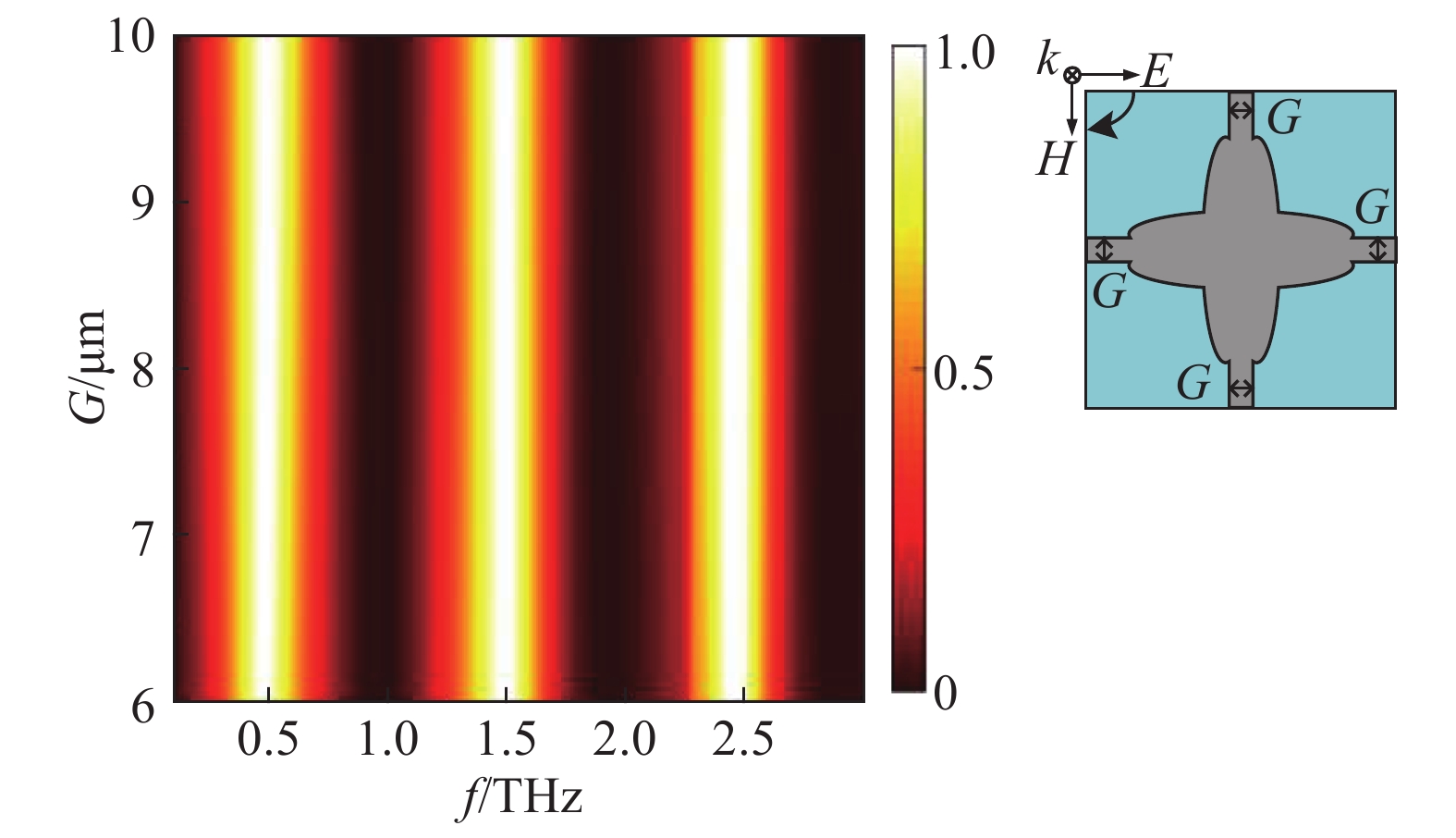
当石墨烯的费米能级为0.9 eV时,十字交叉臂的宽度G对吸收光谱的影响如图11所示. 有趣的是,当参数G从6 μm逐渐增加至10 μm时,吸收峰处所对应的频率和幅值均未出现明显的变化特征,考虑到实际加工中的误差,该现象的出现意味着该器件在实际应用中具有较大的可操作性.
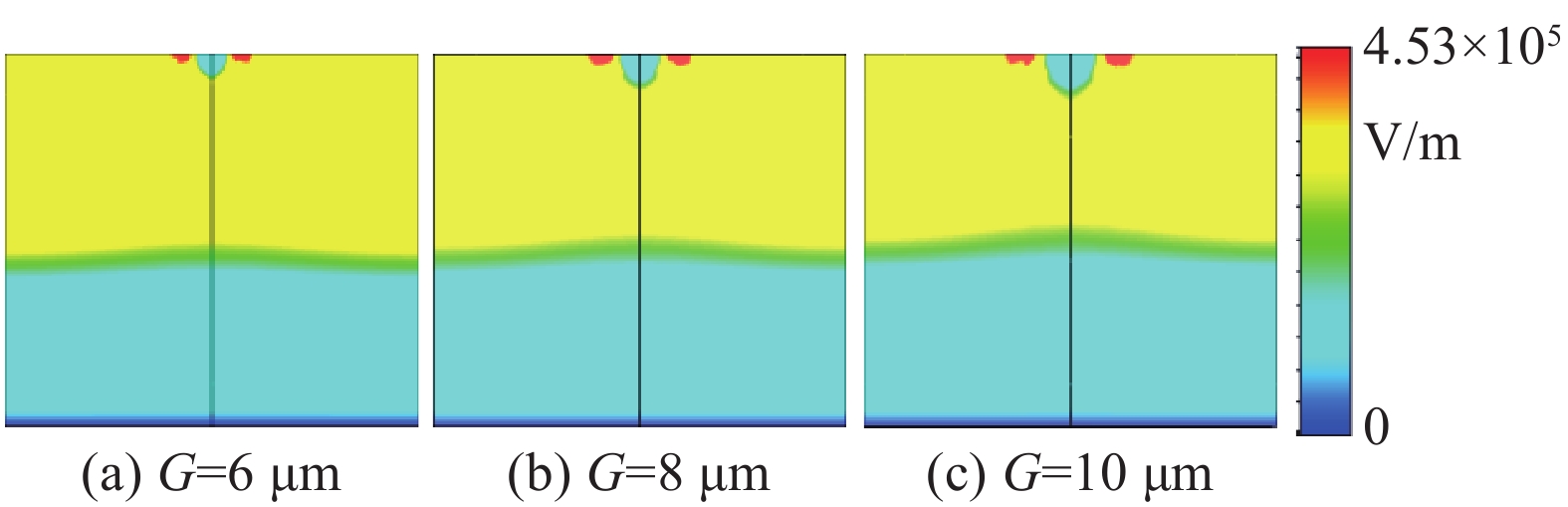
为进一步明确吸收器对结构参数 G 改变的不敏感性,当G分别设置为6 μm、8 μm和10 μm时,共振频率0.489 THz处yoz平面内结构的电场分布如图12所示. 显然,无论参数 G 变化与否,电场均主要集中在石墨烯层与介质层交汇的界面处. 对比图12 (a),(b)和 (c)后可知,石墨烯的表面等离子体共振在参数G (6 μm≤G≤10 μm) 不同的情况下被稳定激发,这是吸收性能保持稳定的关键因素[19, 23].
随后,在图13中分别显示了横向电(transverse electric, TE)和横向磁(transverse magnetic, TM)两种极化模式下太赫兹波斜入射时的吸收光谱. 为便于研究,基于 CST软件的数值模拟可分为以下两种情况:第一种情况是假设电场分量平行于 x 轴,并在 yoz 平面上改变入射波的方向与 z轴之间的夹角
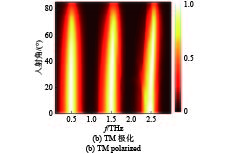
θ ;第二种情况是假设磁分量平行于 y 轴,并在 xoz 平面上改变入射波的方向与 z 轴之间的夹角φ . 事实上,以上两种情况分别对应于TE和TM极化模式. 显然,对于TM极化,当入射角在0°~ 85°变化时,吸收谱中各共振吸收峰的频率范围保持不变,但在65°左右其吸收峰值开始减小并最终消失. 由于吸收的发生与顶层图案化石墨烯上的共振相关,该共振被平行于石墨烯表面的电场激发. 电场的切向分量随着θ 的增加而减小,导致谐振的破坏. 类似的情况也发生在TE极化模式下,但多频吸收带各自的频率范围还随着入射角度的变大而有所增加,这是由于在较大入射角处还发生了一些寄生谐振(parasitic resonance) [18]. 总之,在0°~65°的宽入射角范围内所提出的三频段超材料吸收器的吸收光谱随着入射角度的增加均能保持良好的吸收性能.3 结 论
在本文中,设计并研究了一种基于石墨烯的三频段太赫兹超材料完美吸收器的有效设计方案. 数值仿真结果表明,当石墨烯的费米能级固定为0.9 eV时,所设计的三频段完美吸收器分别在
0.489 THz、1.492 THz和2.437 THz处实现了幅值达到100%的完美吸收效果. 相关的吸收机制可利用阻抗匹配理论和电场分布进行解释. 另外,通过改变石墨烯的费米能级,可有效实现同频范围内三频段吸收谱幅值的有源可调性. 同时,验证了所提出的吸收器结构具有极化不敏感特性,并在0°~65°的宽入射角范围内均保持着良好的吸收性能. 由于其采用设计简单的耦合图案化石墨烯结构,对太赫兹波实现了诸多的可操控特性。因此,所设计的太赫兹功能器件在传感、检测以及光电开关等方面存在潜在的应用前景. -
-
[1] LANDY N I, SAJUYIGBE S, MOCK J J, et al. Perfect metamaterial absorber[J]. Physical review letters,2008,100(20):207402. doi: 10.1103/PhysRevLett.100.207402
[2] WEN Q, ZHANG H, XIE Y, et al. Dual band terahertz metamaterial absorber: design, fabrication, and characterization[J]. Applied physics letters,2009,95(24):241111. doi: 10.1063/1.3276072
[3] ZHANG X, BINGHAM C M, SHREKENHAMER D, et al. A dual band terahertz metamaterial absorber[J]. Journal of physics, D. applied physics: a Europhysics journal,2010,43(22):225101-225102. doi: 10.1088/0022-3727/43/22/225101
[4] HE X, WANG Y, WANG J, et al. Dual-band terahertz metamaterial absorber with polarization insensitivity and wide incident angle[J]. Progress in electromagnetics research,2011,115:381-397. doi: 10.2528/PIER11022307
[5] 崔子健, 王玥, 朱冬颖, 等. 太赫兹超材料吸收器的完美吸收条件与吸收特性[J]. 中国激光,2019,46(6):231-236. doi: 10.3788/CJL201946.0614023 CUI Z J, WANG Y, ZHU D Y, et al. Perfect absorption conditions and absorption characteristics of terahertz metamaterial absorber[J]. Chinese journal of lasers,2019,46(6):231-236. (in Chinese) doi: 10.3788/CJL201946.0614023
[6] HUANG X, HE W, YANG F, et al. Polarization-independent and angle-insensitive broadband absorber with a target-patterned graphene layer in the terahertz regime[J]. Optics express,2018,26(20):25558. doi: 10.1364/OE.26.025558
[7] 高红, 延凤平, 谭思宇, 等. 基于有图案石墨烯的超薄宽带太赫兹超材料吸收体的设计[J]. 中国激光,2017,44(7):237-243. GAO H, YAN F P, TAN S Y, et al. Design of ultra-thin broadband terahertz metamaterial absorber based on patterned graphene[J]. Chinese journal of lasers,2017,44(7):237-243. (in Chinese)
[8] ZHANG Y, SHI Y, LIANG C. Broadband tunable graphene-based metamaterial absorber[J]. Optical materials express,2016,6(9):3036. doi: 10.1364/OME.6.003036
[9] LI J S, SUN J Z. Umbrella-shaped graphene/Si for multi-band tunable terahertz absorber[J]. Applied physics B,2019,125(9):183. doi: 10.1007/s00340-019-7293-x
[10] WANG F L, HUANG S, LI L, et al. Dual-band tunable perfect metamaterial absorber based on graphene[J]. Applied optics,2018,57(24):6916. doi: 10.1364/AO.57.006916
[11] LI J, YAN D, SUN J. Flexible dual-band all-graphene-dielectric terahertz absorber[J]. Optical materials express,2019,9(5):2067. doi: 10.1364/OME.9.002067
[12] HUANG M, CHENG Y, CHENG Z, et al. Based on graphene tunable dual-band terahertz metamaterial absorber with wide-angle[J]. Optics communications,2018,415:194-201. doi: 10.1016/j.optcom.2018.01.051
[13] YAO G, LING F, YUE J, et al. Dual-band tunable perfect metamaterial absorber in the THz range[J]. Optics express,2016,24(2):1518. doi: 10.1364/OE.24.001518
[14] 周译玄, 黄媛媛, 靳延平, 等. 石墨烯太赫兹波段性质及石墨烯基太赫兹器件[J]. 中国激光,2019,46(6):138-157. doi: 10.3788/CJL201946.0614011 ZHOU Y X, HUANG Y Y, JIN Y P, et al. Terahertz properties of graphene and graphene-based terahertz devices[J]. Chinese journal of lasers,2019,46(6):138-157. (in Chinese) doi: 10.3788/CJL201946.0614011
[15] XING R, JIAN S. A dual-band THz absorber based on graphene sheet and ribbons[J]. Optics & laser technology,2018,100:129-132.
[16] WU S, LI J. Hollow-petal graphene metasurface for broadband tunable THz absorption[J]. Applied optics,2019,58(11):3023. doi: 10.1364/AO.58.003023
[17] ZHANG Y, LI Y, CAO Y, et al. Graphene induced tunable and polarization-insensitive broadband metamaterial absorber[J]. Optics communications,2017,382:281-287. doi: 10.1016/j.optcom.2016.08.003
[18] HU N, WU F, BIAN L, et al. Dual broadband absorber based on graphene metamaterial in the terahertz range[J]. Optical materials express,2018,8(12):3899. doi: 10.1364/OME.8.003899
[19] DING F, DAI J, CHEN Y, et al. Broadband near-infrared metamaterial absorbers utilizing highly lossy metals[J]. Scientific reports,2016,6(1):39445.
[20] PIPER J R, FAN S H. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance[J]. Acs photonics,2014,1(4):347-353. doi: 10.1021/ph400090p
[21] MOU N, SUN S, DONG H, et al. Hybridization-induced broadband terahertz wave absorption with graphene metasurfaces[J]. Optics express,2018,26(9):11728. doi: 10.1364/OE.26.011728
[22] ZHAO Y T, WU B, HUANG B J, et al. Switchable broadband terahertz absorber/reflector enabled by hybrid graphene-gold metasurface[J]. Optics express,2017,25(7):7161. doi: 10.1364/OE.25.007161
[23] ZHAO Y, HUANG Q, CAI H, et al. A broadband and switchable VO2-based perfect absorber at the THz frequency[J]. Optics communications,2018,426:443-449. doi: 10.1016/j.optcom.2018.05.085
-
期刊类型引用(2)
1. 袁浩,马燕燕. 双频可调谐超材料吸收器的设计. 山西大学学报(自然科学版). 2022(06): 1530-1535 .  百度学术
百度学术
2. 雷晓勇,霍树云,李燕,王蒙军,孙喆,于河源,李尔平. 小型化超材料吸波体设计与电磁吸收分析. 电波科学学报. 2021(06): 896-904 .  本站查看
本站查看
其他类型引用(3)




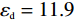
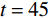
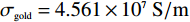
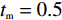
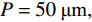
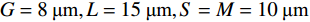
 下载:
下载: