0   引　言

海杂波是指雷达照射波与海面相互作用的后向散射回波^[1]. 在对海雷达目标检测应用中，海杂波使信杂(噪)比恶化，导致“小”目标检测困难^[2]，海杂波谱的漫散导致“慢”目标难以提取，其复杂多变和“海尖峰”现象导致虚警率升高^[3-4]等. 因此，为改善和提高海杂波背景中雷达目标检测能力，海杂波特性认知就成为一项极其重要的工作^[5-6].

真实环境下的雷达海面回波测量是实现海杂波特性认知的重要途径. 自雷达出现以来，人们就陆续开展了海杂波实验观测研究，最具代表性的是美国海军研究实验室（United States Naval Research Laboratory, NRL）在20世纪60年代后期开展的大规模机载雷达海杂波测量实验，采用工作在UHF、L、C和X波段的机载4波段雷达，在波多黎各、北大西洋等海域录取了大量的海杂波数据，用于海杂波特性研究^[7-8]. 1994年，美国国防部高级研究计划局（Defense Advanced Research Projects Agency, DARPA）和美国海军共同发起地海杂波测试的“山顶计划”^[9]，为预警机雷达空时自适应信号处理算法提供了杂波数据支持. 1991年，加拿大McMaster大学在东海岸采用IPIX雷达开展常年海杂波观测，形成的海杂波数据样本被学界广泛使用^[10]. 2006年以来，澳大利亚国防与科技机构先后开展了S波段和L波段的多通道多极化海杂波测量，支持陆海交界的海杂波特性研究^[11-12]. 国内除了结合雷达科研任务开展的少量海杂波数据录取外，中国电波传播研究所对海杂波开展了系统性研究，自20世纪以来相继建立了车载、船载、机载、塔基等多种平台的海杂波测量系统^[13-17]，获取了大量复杂海情海杂波实测数据，用于海杂波特性研究及应用^[18-19].

海杂波建模是寻求建立海杂波特性与雷达参数和海洋环境参数间的关联关系，以掌握海杂波时空变化规律^[20-22]. 传统的建模方法是基于海杂波实测数据，利用数理统计方法，建立相关参数化模型. 对于海杂波散射系数，基于Nathanson等人的平均后向散射系数数据集^[23]，国外学者相继建立了SIT模型、GIT模型、TSC模型、HYB模型、NRL模型等经验或半经验模型^[24]. 对于海杂波幅度分布，英国学者Watts等人^[25]针对海杂波的幅度统计K分布模型，基于X波段机载高分辨海杂波数据，建立了形状参数、雷达擦地角、方位角以及分辨单元面积等参数的经验模型. 对于海杂波多普勒谱，Walker^[26-27]利用造浪池数据建立了一种同时考虑布拉格、白浪和破碎3种散射机制的三分量平均多普勒谱模型；Ward等人^[28]借鉴复合K分布幅度建模思想，提出利用两个高斯函数对谱形状进行描述的短时多普勒谱建模方法；Rosenberg^[29]提出了一种能够描述时间和空间谱特性变化的多普勒谱参数化模型，该模型同时考虑了雷达分辨单元和积分时间对多普勒谱参数的影响. 利用我国海杂波实测数据，中国电波传播研究所分别建立了适用于L波段的海杂波散射系数修正GIT模型^[30-31]、UHF波段的修正TSC模型^[32-33]、S波段的修正NRL模型以及小擦地角的海杂波幅度分布模型等^[34-35]；针对海杂波平均多普勒谱和短时多普勒谱建模过程中存在的散射机制考虑不全、长短时不统一的问题，建立了基于不同散射机制特征的海杂波时变多普勒谱模型^[36-37].

近年来，快速发展的机器学习/深度学习技术^[38]在多个领域得到了广泛应用，该技术尤其擅长高度复杂、多参数、非线性关系的关联建模问题，这为海量海杂波数据处理和特性建模提供了新途径. 2008年，Mezache等人^[39]尝试利用模糊神经网络（fuzzy neural network, FNN）方法进行海杂波K分布形状参数的估计，神经网络的输入为由最大似然或矩估计方法得到的形状参数. 然而，当海杂波数据中存在热噪声时，K分布的形状参数、尺度参数和热噪声功率必须同时进行估计，因此估计结果不理想. 2013年，该团队^[40]为了提高海杂波RiIG（Rician Inverse Gaussian）分布模型参数的估计性能，基于RiIG分布的累积分布函数（cumulative distribution function, CDF）的逆函数，利用人工神经网络（artificial neural network, ANN）进行了参数估计，网络的输入为海杂波实测数据的CDF回归曲线. 实验数据表明，相对于标准迭代最大似然估计方法，基于该方法估计的参数可以更好地拟合真实海杂波数据的CDF和概率密度函数(probability density function, PDF). 2015年，Machado-Fernández等人^[41]提出了一种海杂波Weibull分布形状参数的神经网络估计方法，相对传统的矩估计方法，该方法的参数估计精度更高，且更适合于真实杂波环境的Weibull分布形状参数实时估计. 2016年，该团队^[42]又基于神经网络和深度学习理论，提出了一种海杂波K分布形状参数估计的新方法. 该方法基于9个独立训练的神经网络组合体，可实现与传统矩估计方法同样速度的参数估计，且在K分布形状参数较小的情况下估计精度更高. 中国电波传播研究所基于长期实验测量的海杂波大数据集，将深度学习方法引入到海量海杂波数据处理^[43]和海杂波特性的智能建模^[44-46]，提升了海杂波散射系数、幅度分布和多普勒谱等特性的精细化认知能力^[47].

本文从海杂波的测量、数据处理和特性建模三方面对中国电波传播研究所相关课题组近年来的研究进展进行综述. 第1节介绍海杂波测量技术，重点简述几种典型的海杂波测量系统. 第2节介绍海杂波数据处理技术，重点介绍基于深度学习网络的海杂波原始数据处理方法和海杂波特性提取方法. 第3节介绍海杂波特性建模方法，分别介绍了基于统计意义的经验建模方法和深度学习建模方法. 最后，对海杂波研究未来发展方向进行了展望.

1   海杂波测量技术

海杂波测量是获取海杂波数据进而开展海杂波特性研究的重要手段. 原理上讲，任何一部目标探测雷达均可用于海杂波测量，然而，若不作适当改进、定标以及按一定要求测量，那么获得的测量数据对于海杂波特性研究及应用而言，有可能没有任何实质性意义.

1.1   海杂波测量原理

1.1.1   基本方程

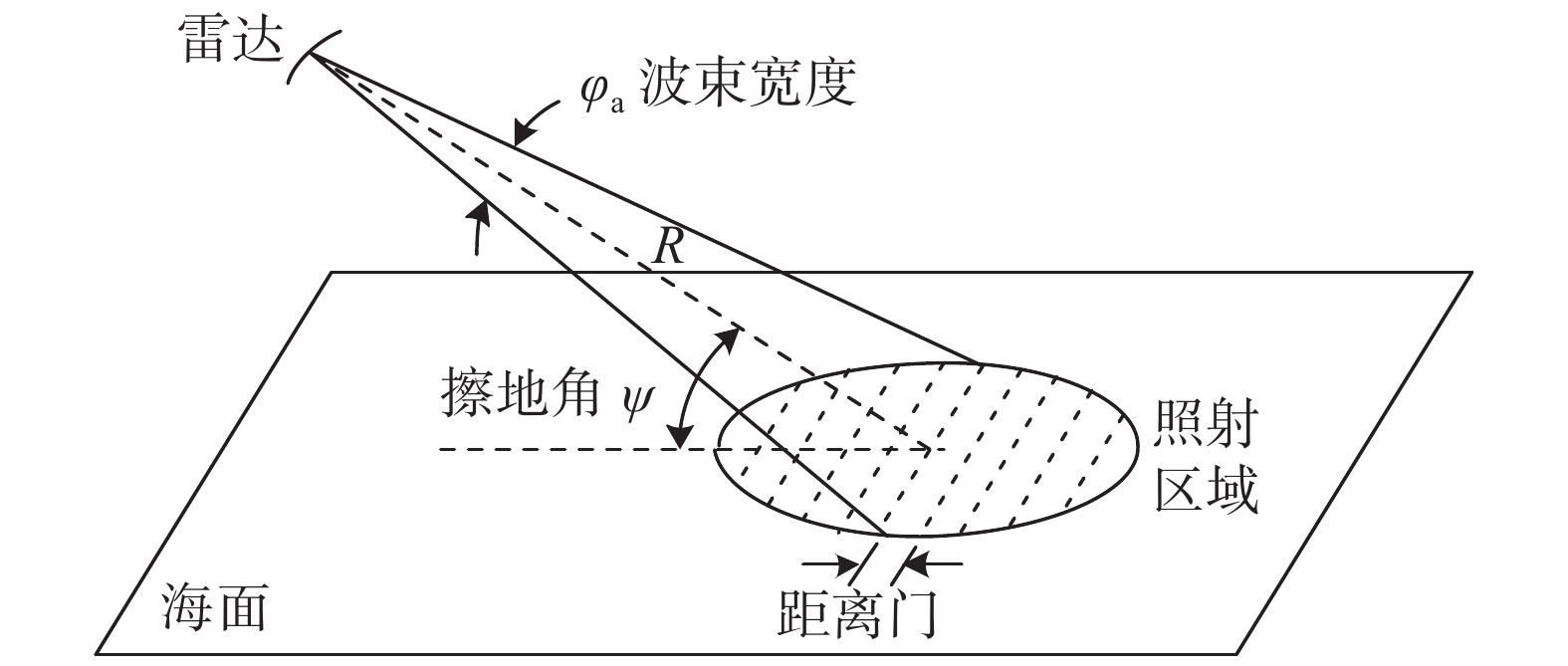
如图1所示，在不考虑系统损耗和传播效应的情况下，单站（单基地）雷达系统的雷达方程为

式中：${P_{\text{r}}}$为雷达接收功率；${P_{\text{t}}}$为雷达发射功率；$G$为雷达天线增益；$\lambda$为雷达波长；$R$为目标至雷达天线的距离；$\sigma$为目标雷达散射截面积(radar cross section, RCS).

图  1  海杂波测量示意图

Fig.  1  Schematic of sea clutter measurement

下载: 全尺寸图片 幻灯片

海面属于面目标，其RCS可表示为$\sigma^{\text{o}} \cdot A$，$\sigma^ {\text{o}}$为单位表面积的RCS（又称散射系数），$A$为雷达波束照射在海面的面积. 代入式(1)得到

式(2)即为海杂波测量的基本方程.

对于脉冲压缩体制，不能直接使用式(2)，而须采用下式：

式中：$\;\rho = {\tau _{\text{t}}}/{\tau _{\text{c}}}$为脉冲压缩比，${\tau _{\text{t}}}$为脉压前的脉冲宽度，${\tau _{\text{c}}} = 1/B$为脉压后的脉冲宽度，$B$为带宽；$A$为脉压后的照射面积.

1.1.2   测量平台

面向雷达不同的应用场景，海杂波测量可包括岸基、船载、机载、星载等不同的测量平台. 不同测量平台首先要满足测量所需要的远场条件，即海面散射单元与天线间的距离满足

式中：${l_{\text{t}}}$和${l_{\text{a}}}$分别为散射单元和天线口径的横向尺寸. 对于粗糙海面而言，式(4)可简化为$R > > 2{l^2}/\lambda$，$l$为海面表面粗糙引入的表面相关长度.

其次，需要选择测量平台合适的架设位置. 如对于岸基平台通常要求面向开阔海域，远离陆海交界区域，且要求具备一定的架设高度，实现尽可能大擦地角范围内的海杂波测量. 对于船载平台通常要求雷达照射的海面区域距离船只不小于500 m，以避免船体附近的海浪影响，且需要配备稳定平台，避免船只晃动导致雷达波束指向的起伏，影响海杂波测量的稳定性.

1.1.3   外定标

外定标是海杂波测量的一个重要环节. 外定标可获得海面散射回波的绝对值，使得测量数据具有推广应用价值. 对于真实环境下的单站雷达，在考虑损耗和传播效应的情况下，其雷达方程为

式中：F为路径上的方向图传播因子；L为系统双程损耗即系统定标常数，其他参数与式(1)相同. 当雷达参数、$\sigma$已知时，可以根据雷达接收功率得到系统常数，即

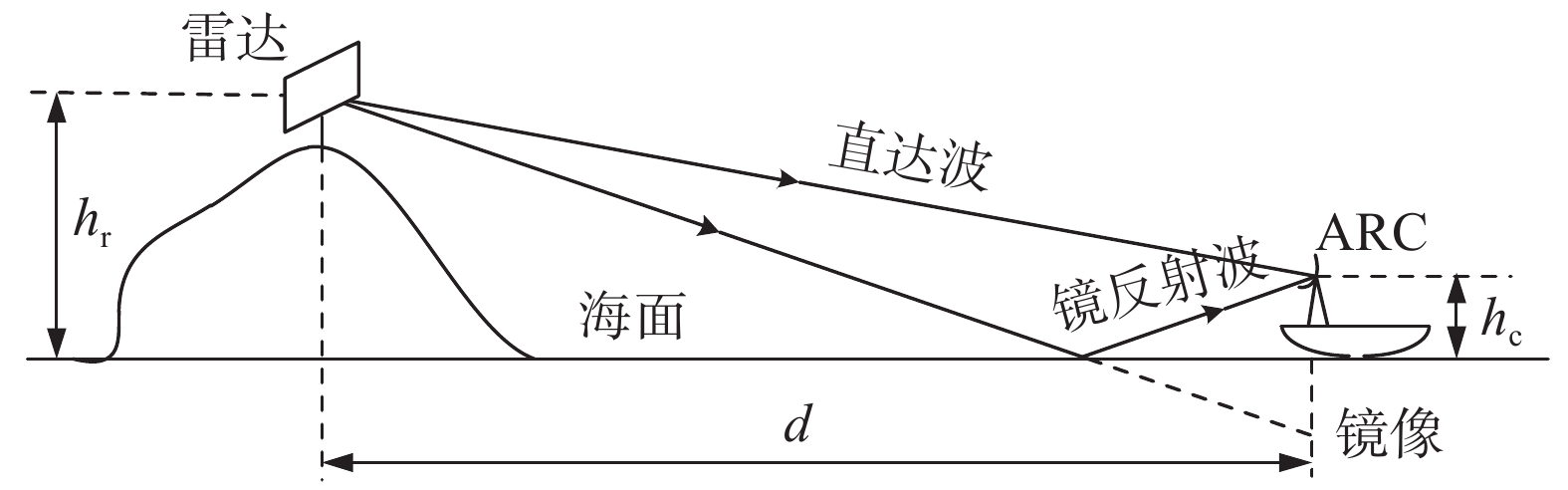
外定标技术是用已知$\sigma$的定标体（也称校准体）的回波信号，实现对雷达系统的定标. 通常，校准体可分为无源和有源两种：无源校准体主要包括平板、球体、角反射器和龙伯透镜等；有源校准体最常用的是有源定标器（active radar calibrator, ARC）. 相比无源外定标，有源外定标的优点是RCS可调. 实际中，要求外定标具有足够的信杂比（通常为20 dB以上）的同时，还需考虑架设平台、多径等的影响. 黎鑫等^[48]针对岸基海杂波测量平台，提出了一种海上外定标方法. 如图2所示，将ARC架设在小型船只上，通过船载稳定平台减小船只晃动影响. 同时根据多径传播模型，考虑多径影响，到达ARC接收天线的电场认为是直射波、镜反射波和漫散射波的总和，即

式中：${E_0}$为直达波的场强；$\; {\rho _{\text{s}}}$为海面的粗糙度衰减因子；$\varGamma$为菲涅尔反射系数；$\varphi$为镜反射波的相位，${\varphi}{\text{ = }}\dfrac{{2{\text{π}} \Delta R}}{\lambda }$，$\Delta R$为直达波和反射波传播路径差；${E_{\text{d}}}$为漫反射波场强（幅度上服从Rayleigh分布，可表示为${\varGamma _{\text{d}}}{E_0}$，${\varGamma _{\text{d}}}$为漫反射系数）；$\phi$为漫反射场随机相位（服从$- {\text{π }}$到${\text{π }}$的均匀分布）.

粗糙度衰减因子$\;{\rho _{\text{s}}}$可表示为

式中：${h_{{1/3}}}$为海面有效波高；${h_{\text{s}}}$为测量船周围海面的高度，其他参数含义见图2.

图  2  岸基海杂波测量雷达外定标示意图^[48]

Fig.  2  External calibration diagram of shore-based sea clutter measurement radar^[48]

下载: 全尺寸图片 幻灯片

路径差$\Delta R$是产生相位差异的重要原因，而海面高度${h_{\text{s}}}$对路径差$\Delta R$的影响不可忽略，可表示为

式（10）中，假定船只所在的海面和间接波的反射面相对于海平面具有相同的高度${h_{\text{s}}}$，且${h_{\text{s}}}$随涌浪和波浪而变化.

由于漫散射分量只占海面反射信号的很小部分，根据式(7)多径模型，在忽略海面的漫射散射分量时，可以得到雷达与校准器之间路径上的方向图传播因子：

通过式(11)估计得到雷达与ARC之间的传播因子之后，代入式(6)，并基于实验测量的雷达接收功率${P_{\text{r}}}$，即可分析得到定标系统常数L.

1.1.4   信杂比要求

杂波测量雷达有一定的动态范围，其测量的最小值受限于雷达的本底噪声. 假设雷达的噪声系数为${F_{\text{n}}}$，雷达的噪声功率电平可由下式得到：

式中：$k$为波尔兹曼常数，即$1.38 \times {10^{ - 23}}\;{\text{J}}/{\text{K}}$；${T_0} = 290\;{\text{K}}$.

一般常用雷达噪声功率电平作为雷达测量的灵敏度，但当测量的杂波功率与噪声功率平均值相当时，是无法分辨杂波和噪声的，此时的测量值并不能体现杂波水平. 杂波测量值要达到一定的精度，杂波与噪声功率之比即信杂比须满足一定的条件，通常要求大于10 dB.

1.2   海杂波测量系统

一个完整的海杂波测量系统应包括海杂波测量雷达和环境参数辅助测量设备. 海杂波测量雷达可以是专用的测量雷达，也可以是结合任务的目标探测雷达，但两种雷达均需开展外定标. 环境参数辅助测量设备一般包括海浪测量浮标、测风仪、船舶自动识别系统（automatic identification system, AIS）和电磁环境测试设备等，用于获取测量海域的浪高、浪向、风速、风向、温度、含盐度、海上目标回波和周围电磁频谱等，为海杂波分析过程中排除目标回波干扰、电磁环境干扰以及海面状态描述提供基础数据.

经过多年的努力，中国电波传播研究所相继建立了不同平台的海杂波测量系统，本文简要介绍以下几种.

1.2.1   岸基海杂波测量系统

岸基海杂波测量系统位于青岛附近的灵山岛上，由UHF、L、S、X、Ku等5个波段海杂波专用测量雷达和环境参数辅助测量设备组成，测量雷达主要参数如表1所示. 雷达架设在海拔约450 m高处，实现对开阔海域多参数海杂波测量，部分多通道雷达具备仿机载运动功能，可实现空时二维海杂波测量和特性分析^[18]. 此外，通过配置无人目标模拟船，该系统可开展海上目标RCS测量.

表  1  岸基海杂波测量雷达主要参数

Tab.  1  Main parameters of shore-based sea clutter measurement radar

参数	取值
频率	UHF	L	S	X	Ku
带宽	1~10 MHz	1~10 MHz	1~10 MHz	5~50 MHz	5~50 MHz
极化	HH	HH, VV	HH, VV	HH, VV	HH, VV
最大擦地角	北侧方向7°，其他方向17°
最小擦地角	1.22°	1.28°	1.22°	1.26°	1.24°
方位	≤60°	≤210°	≤60°	≤120°	≤120°
平台	机械转动，仿机载运动（IDPCA）			机械转动

下载: 导出CSV 

| 显示表格

目前，灵山岛岸基海杂波测量系统常态化运行，持续积累的海杂波数据已达PB量级，海情覆盖1~6级. 为促进海杂波领域研究，建立了海杂波科研数据开放共享机制，其中部分数据已被国内科研院所和高校使用^[20].

1.2.2   船载海杂波测量系统

为实现不同海域及远海海杂波测量，构建了适用于船载平台的S、X双波段海杂波专用测量雷达（主要参数见表2），配有稳定平台和高精度姿态记录仪. 环境参数辅助测量主要由海面高速摄像仪、船载水文气象设备等获取.

表  2  船载海杂波测量雷达主要参数

Tab.  2  Main parameters of shipborne sea clutter measurement radar

参数	取值
频率	3.2~3.4 GHz	9.5~10.5 GHz
体制	相参脉冲体制	相参脉冲体制
极化	HH	HH、VV
带宽	2.5~20 MHz	5~200 MHz
脉冲重频	500 Hz, 2 kHz, 5 kHz, 10 kHz	500 Hz, 1 kHz, 5 kHz, 10 kHz
脉冲宽度	0.3 μs, 0.5 μs, 0.8 μs, 3 μs	3 μs, 8 μs,30 μs

下载: 导出CSV 

| 显示表格

目前，通过搭载 “琼沙3号”补给船、 “舟桥3号”轮渡船，开展了多个航次的我国南海、东海海域海杂波测量，海情覆盖1~5级，为研究不同海域海杂波特性差异提供了重要基础数据^{[6, 49]}.

1.2.3   塔基海杂波测量系统

岸基和船载平台更适合小擦地角海杂波测量. 为开展大擦地角（擦地角大于60°）海杂波测量，最近构建了基于海上石油钻井平台的塔基海杂波测量系统，其测量雷达主要参数见表3，环境参数辅助测量主要通过测量海区海浪测量浮标、塔基水文气象设备等获取.

表  3  塔基海杂波测量雷达主要参数

Tab.  3  Main parameters of offshore-platform-based sea clutter measurement radar

参数	取值
频率	Ku
发射功率	45 W
极化	HH, VV
天线增益	25 dB
脉冲重频	1 kHz
脉冲宽度	50 ns, 200 ns
波束宽度	7.5°（方位/俯仰）
观测范围	方位：−160°～ +160° 俯仰：−70°～ +10°

下载: 导出CSV 

| 显示表格

该测量系统为开展大擦地角、高海情海杂波特性研究提供了重要基础数据.

2   海杂波数据处理技术

2.1   原始数据处理

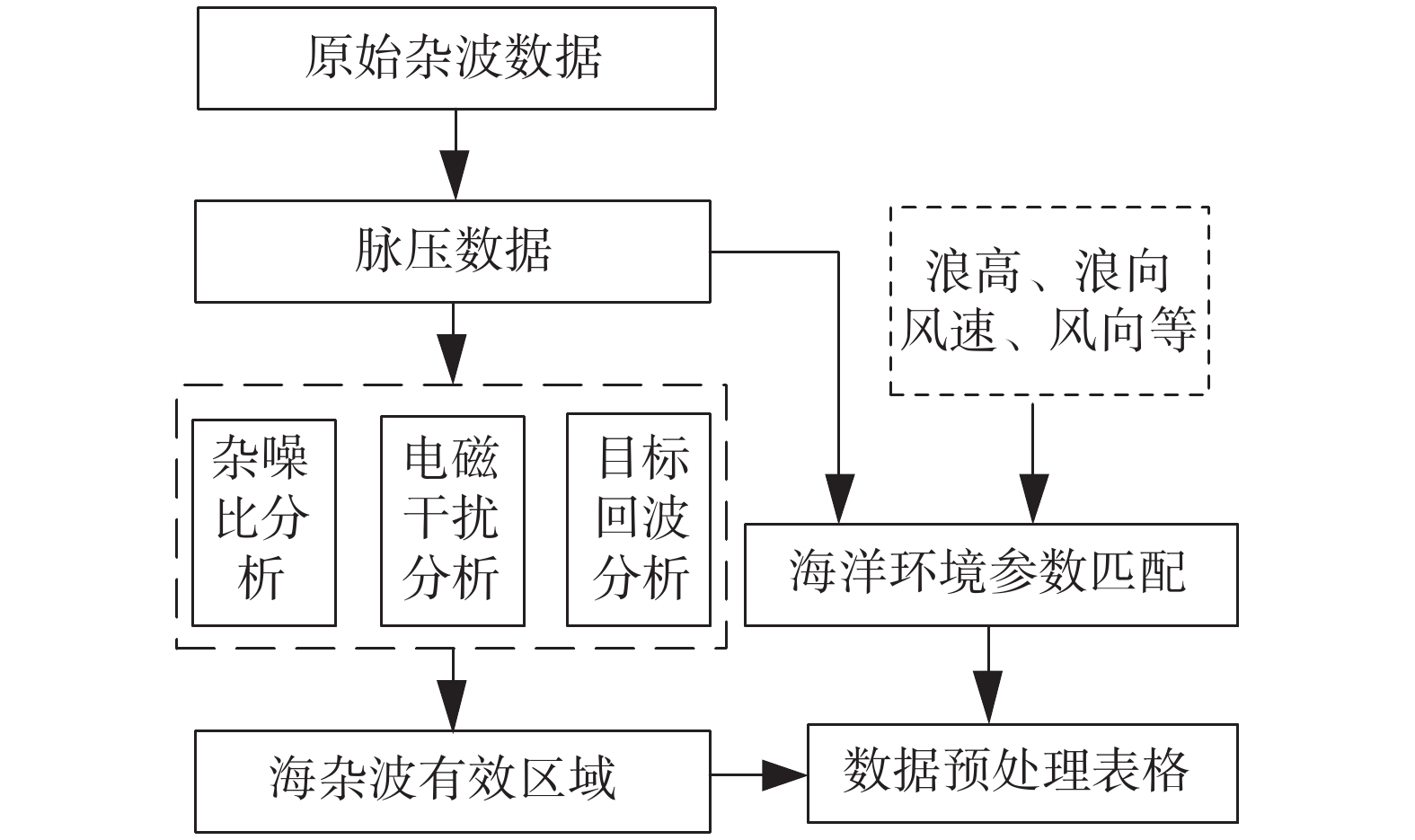
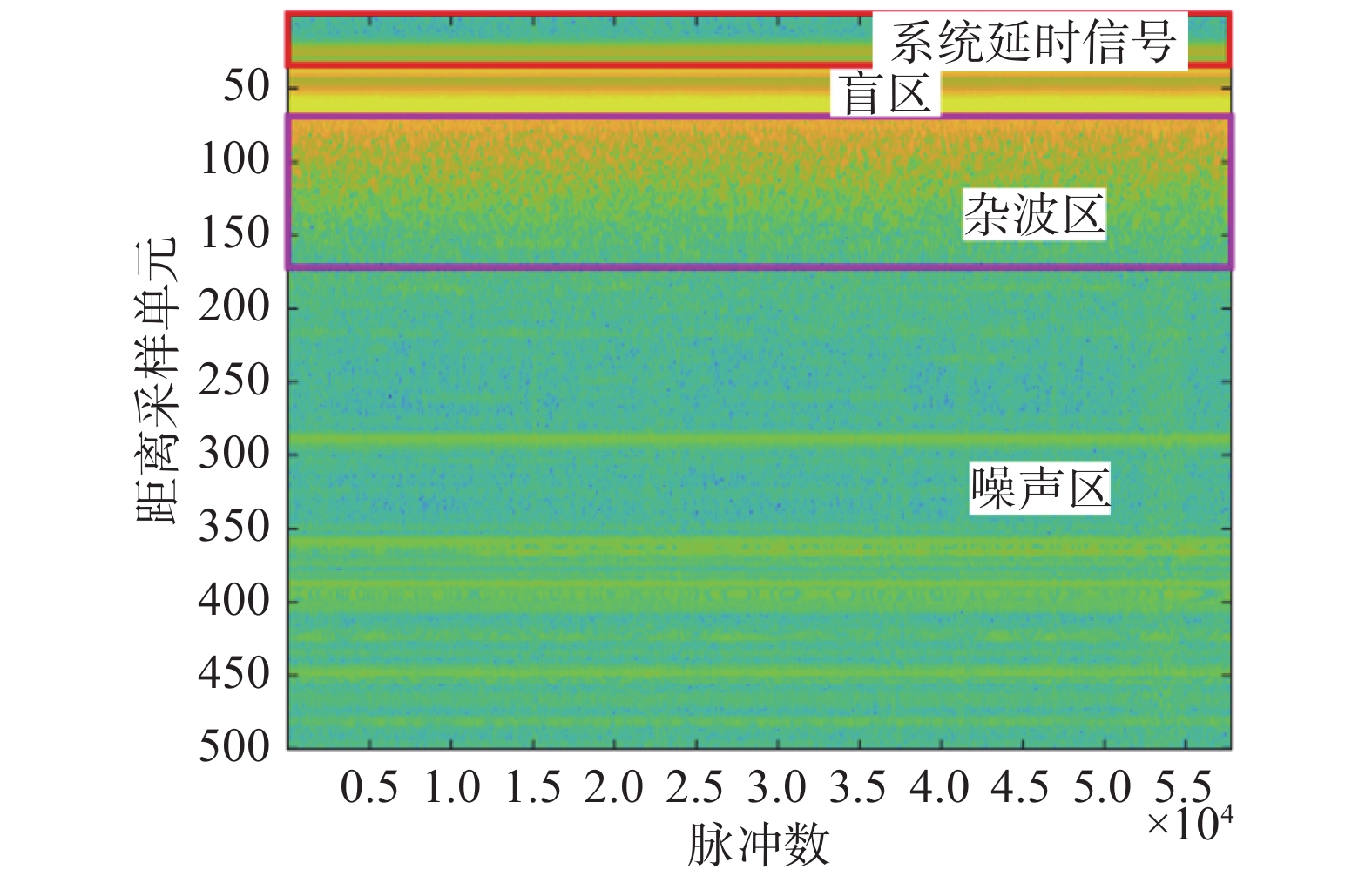
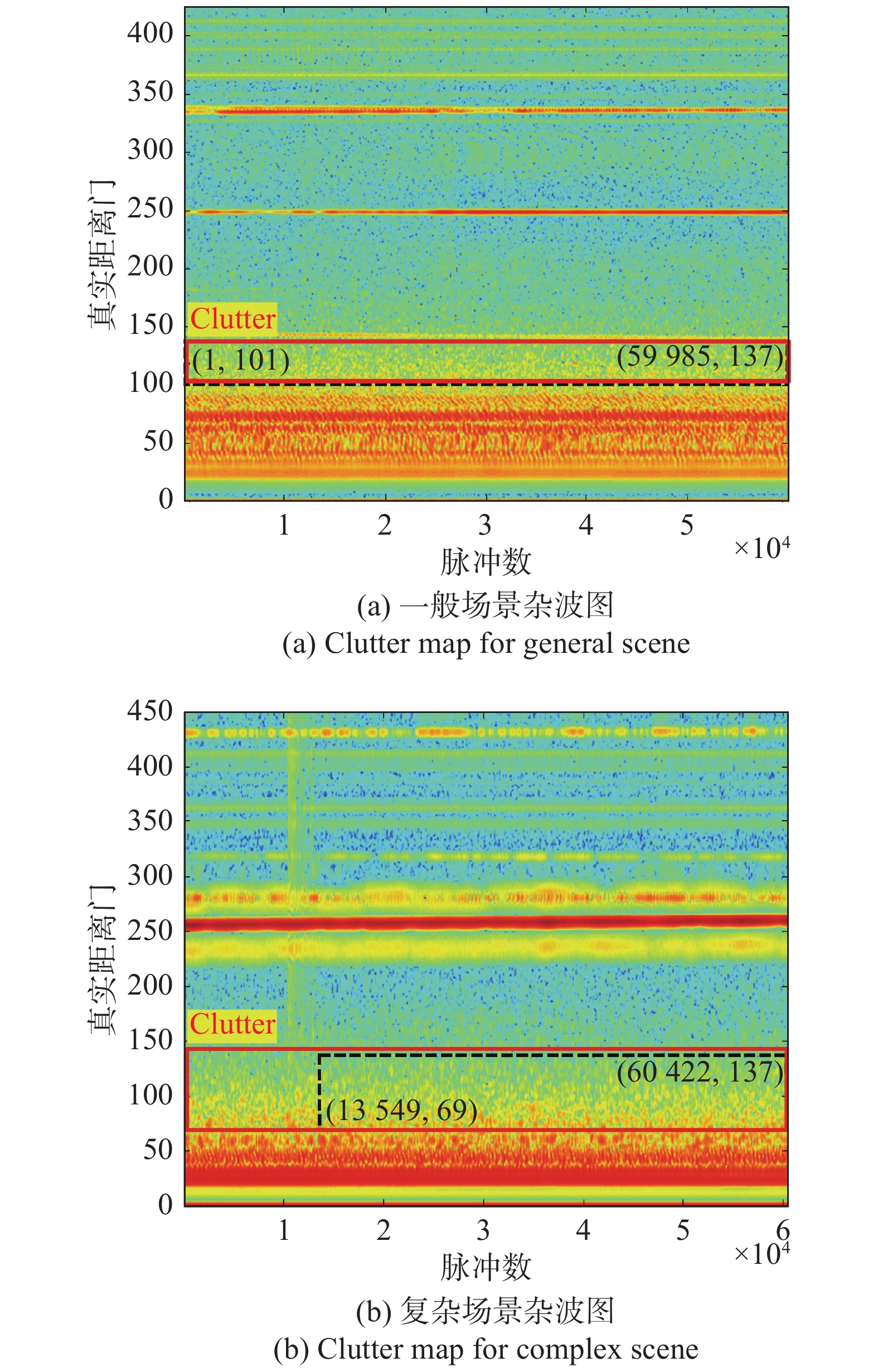
从海面雷达回波原始采样数据中提取纯化的海杂波有效区域，这一过程即为海杂波原始数据处理，其流程如图3所示. 雷达接收机的原始采样数据包括系统时延信号、泄漏信号（或盲区）和雷达回波数据，其中雷达回波数据又可以根据信杂比划分为杂波区（高信杂比）和噪声区（低信杂比），如图4所示.

图  3  雷达回波原始数据预处理流程图

Fig.  3  Flow chart of radar echo raw data preprocessing

下载: 全尺寸图片 幻灯片

图  4  雷达原始脉冲-距离回波图

Fig.  4  Radar range-pluse echo map

下载: 全尺寸图片 幻灯片

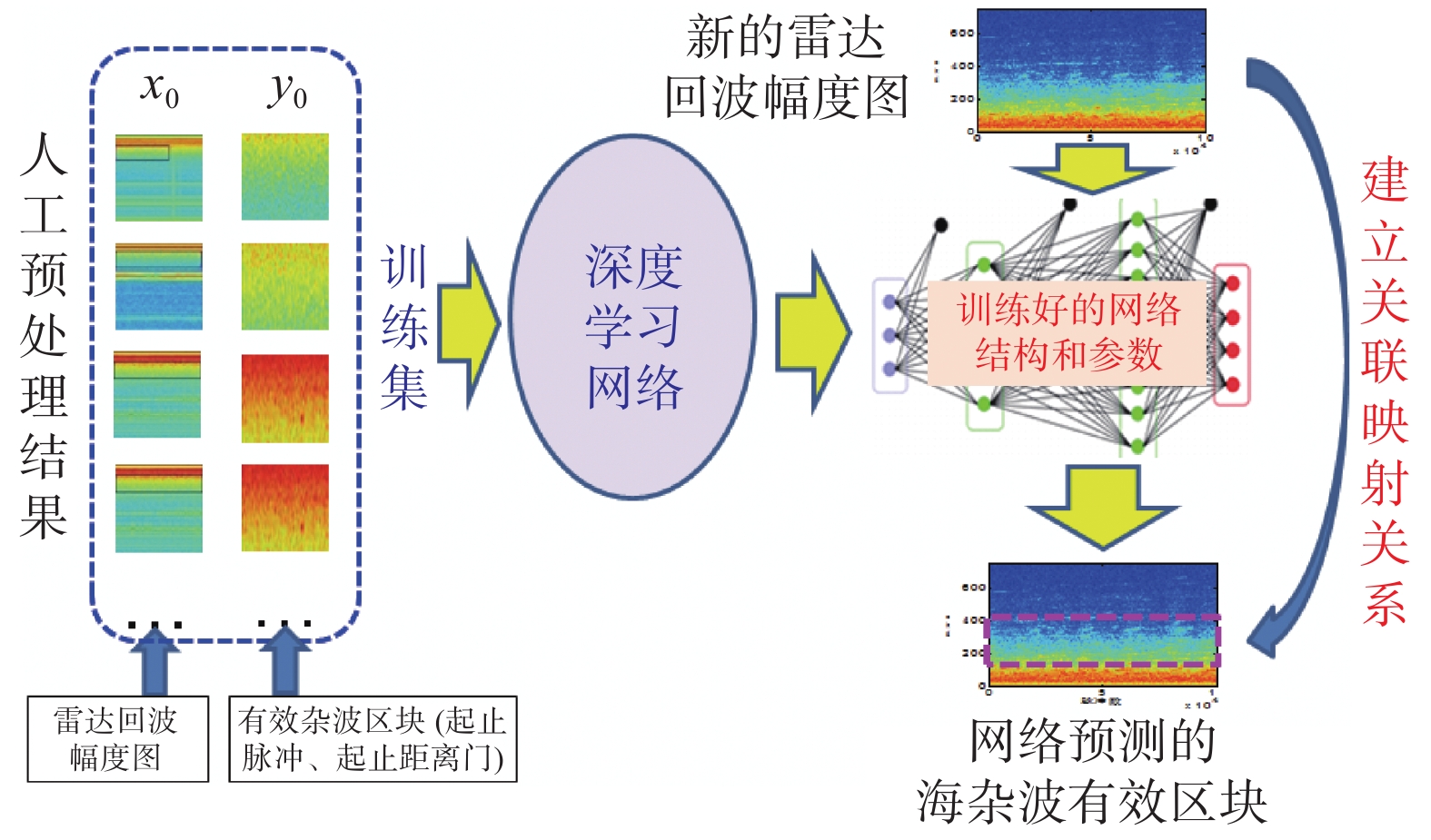
为获取有效杂波区，在传统人工经验方法^[50]的基础上，将从原始雷达回波中提取海杂波有效区域的问题视为一个计算机视觉的图像目标检测问题，采用YOLO目标检测深度学习算法，结合海杂波有效区域的典型特点，实现了基于多表示域特征的海杂波有效区域检测提取^{[43, 45, 51]}，其检测框架如图5所示. 基于深度学习的检测方法，在保持较高准确率的情况下，大幅提高检测效率，大大节省了海量海杂波原始数据处理的人力成本.

图  5  基于深度学习的海杂波有效区域检测框图

Fig.  5  Flowchart of sea clutter effective area detection based on deep learning

下载: 全尺寸图片 幻灯片

雷达海杂波测量中受雷达架设平台高度、雷达波束宽度等影响，海杂波有效区的距离采样数是有限的，而时间采样数则是可以通过增大雷达脉冲重复频率和数据测量时间来增加，导致海杂波的时间采样数通常远大于距离采样数. 另外，从对海杂波特性研究的角度来说，海杂波幅度均值、幅度分布、多普勒谱特性估计都是基于单个距离分辨单元多个时间采样序列进行的，时间采样上少量样本的误判作为异常样本在统计处理中可以剔除，而距离采样上的误判则容易造成将非海杂波数据作为海杂波数据处理，导致结果偏差，因此海杂波有效区提取中对距离维判别准确性的要求高于脉冲维. 基于此，针对海杂波有效区域提取中距离、时间维度损失的不一致问题，将YOLO损失函数中的目标边框坐标预测损失进行修正，通过系数加权的形式增大距离维上的损失贡献，其损失函数形式为

式中：${L_x},{L_y}$分别为矩形边框左下点坐标$x,y$的位置预测损失；${L_w},{L_h}$分别为矩形边框宽度（w）和高度（h）的预测损失；$\;{\rho _x}, {\rho _y}$为加权系数；x轴为脉冲维；y轴为距离维.

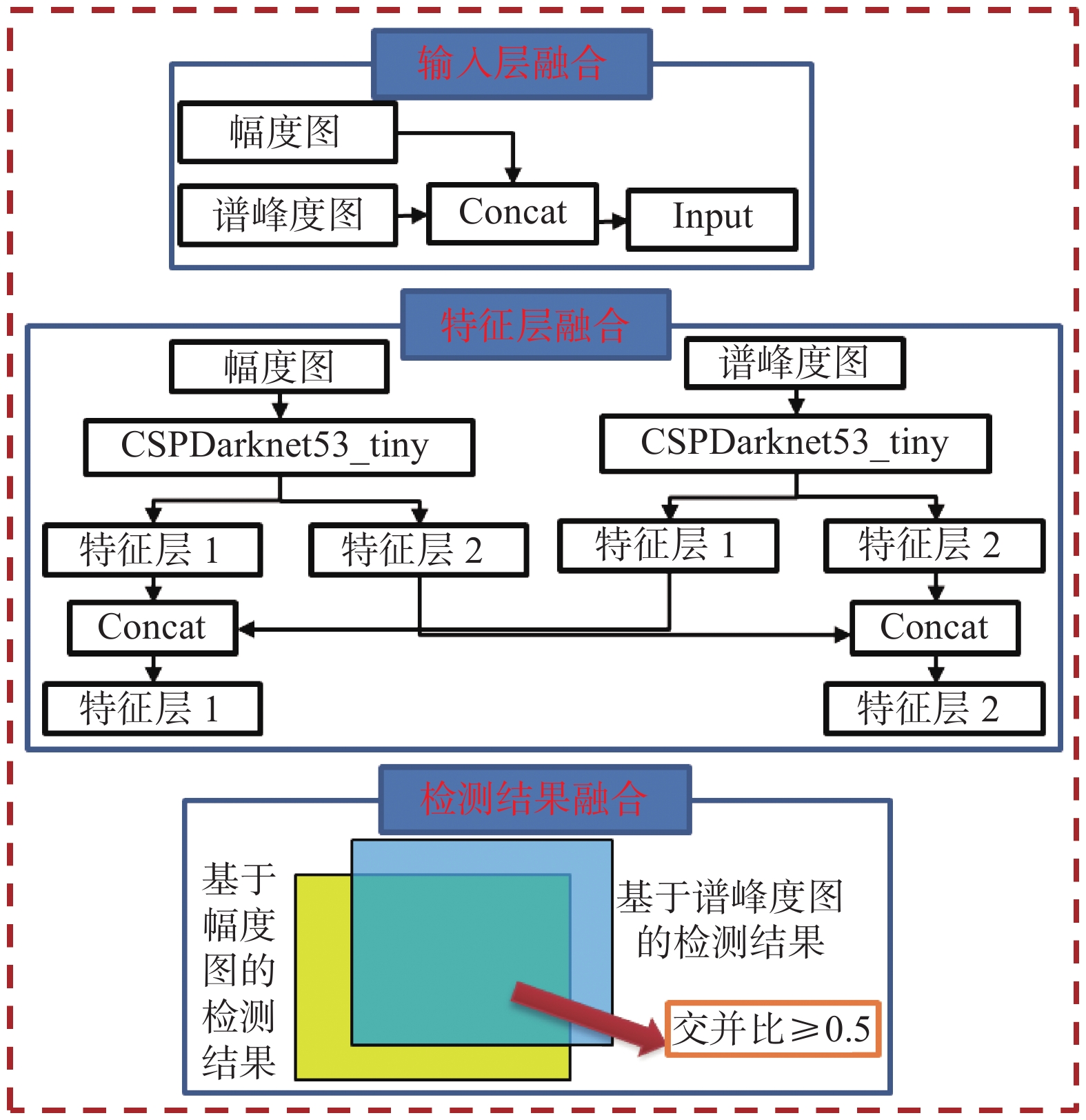
分析雷达回波的幅值图与功率谱峰度图发现，幅度图中杂波和噪声的边界更清晰，而功率谱峰度图中杂波和干扰的边界更清晰. 不同信号间的边界越清晰越有利于提高图像目标检测的精度. 为此，将海杂波幅值图与功率谱峰度图特征融合，并分为3个层次：像元级、特征级和决策级（如图6所示），实现海杂波有效区域的检测^[51]. 像元级融合实现在网络输入层，将多特征图像的R、G、B通道进行累叠，增加输入通道数；特征级融合采用CSPDarknet53_tiny基础网络并行处理的方式，将提取的特征数据进行多通道累叠融合；决策级融合将分别基于幅值图的检测结果与基于功率谱峰度图的检测结果进行融合，两个结果的补集作为最终的检测结果，避免单一特征的漏检问题.

图  6  基于多表示域特征的有效区域检测网络构建流程图^[51]

Fig.  6  Flow chart of sea clutter effective area detection based on multiple representation domain features^[51]

下载: 全尺寸图片 幻灯片

图7给出了两组典型的灵山岛S波段海杂波数据情况下，基于Yolov4 tiny网络结构的有效区检测结果对比图. 从图7(a)中可以看出，在一般场景海杂波数据情况下，由于海杂波有效区附近的目标干扰和电磁同频干扰较少，因此网络预测区域与真实区域吻合较好. 在复杂场景（图7(b)）的杂波数据情况下，存在较多的强目标信号，且存在大量同频干扰信号（表现为竖条纹），与海杂波区域在幅值强度上产生混淆，导致海杂波有效区检测结果偏离真实杂波区. 经过不同海情的检测结果统计，对于像元级、特征级和决策级融合，其平均检测准确率分别为86.26%、86.33%和91.57%.

图  7  海杂波有效区域检测结果

注：黑色虚线框表示真实的海杂波有效区；红色实线框 （clutter）表示检测网络得到的海杂波有效区.

Fig.  7  Detection results of sea clutter effective area

下载: 全尺寸图片 幻灯片

2.2   海杂波特性提取

在得到海杂波有效区之后，即可开展海杂波散射系数、幅度分布、多普勒谱等特性数据提取. 对于散射系数，首先由外定标数据得到测量雷达的系统常数；然后利用海杂波有效区数据和雷达参数，由雷达方程求得每个距离门和脉冲对应的散射系数；最后，针对不同的距离门（即擦地角）求出多个脉冲对应的散射系数均值，即得到海杂波幅度均值，该均值为实际中常用的海杂波散射系数.

对于幅度分布，提取步骤包括：① 针对某一确定距离门，提取N个脉冲的幅度大小并进行均值归一化${x \mathord{\left/ {\vphantom {x {\left\langle x \right\rangle }}} \right. } {\left\langle x \right\rangle }}$；② 按照一定的幅度值步长区间，统计每个区间内的频次，得到实测数据的概率密度分布图；③ 利用不同的统计分布函数形式，对实测概率密度分布图进行函数拟合，并进行拟合优度检验^[52]，拟合最好的函数形式即为该距离门海杂波服从的统计分布形式；④ 针对该最优统计分布形式，采用不同的参数估计方法，如最大似然估计、矩估计等^[1]，估计得到该函数形式对应的参数，即为该距离门海杂波服从的统计分布参数；⑤ 针对其他距离门数据，循环上述步骤，提取得到相应的幅度统计分布特性.

海杂波的多普勒谱特性可以表现为长时平均多普勒谱和短时多普勒谱，两者的主要区别在于谱估计的时间长短不同，前者通常在秒量级，后者通常在毫秒量级. 因此，在基于海杂波有效区提取谱特性时，须首先确定谱类型，并设定谱估计的时间T；其次，针对某一距离门，选用周期图法或是Welch等现代谱估计方法，利用T时间内的海杂波时间序列数据开展谱估计，得到多普勒谱形状曲线；最后，基于该谱形状曲线，采用在高斯型和立方型杂波功率谱估计中性能较优的“质心法”，计算得到多普勒频移和展宽. 针对其他的距离门和谱估计时段，循环采用上述方法，估计得到相应的谱形状和谱参数.

3   海杂波特性建模

海杂波特性建模指的是建立海杂波特性与海杂波影响因素之间的映射关系. 由于海面状态时空变化复杂，海面回波与雷达参数和海洋环境参数之间存在着非线性依赖关系，导致准确建立这些参数与海杂波之间的联系成为难题，特别是当雷达工作在小擦地角状态下，海杂波特性更加复杂.

3.1   经验建模

利用海杂波实测数据，采用数理统计方法得到的海杂波特性与雷达参数、环境参数之间的数学表达式，即为海杂波经验模型.

3.1.1   散射系数建模

国外学者利用实测数据，相继建立了SIT、GIT、TSC、HYB、NRL等散射系数经验或半经验模型^[24]. 这些模型由于数据来源不同，采用的输入参数不同，多数情况下相互间不存在可比性，或者说存在较大误差，导致实际应用中模型选择的不确定性^[1].

中国电波传播研究所基于大量的海杂波实测数据，对上述模型的适应性进行了检验，并据此提出了修正GIT模型^[30]和修正NRL模型^[1].

实际应用中发现，GIT模型在较低风速和较高风速情况下散射系数均偏小. 经分析，缘于模型中的风速因子设置问题. 引入两个临界风速因子和两个相对斜率调整因子，即

式中：${v_{{\rm{w}}} }$为风速；相对斜率$\; {\rho _1} > 0,\;{\rho _2} > 0\;$；临界风速$v_2^{\text{c}} > v_1^{\text{c}} > 0$. 相对于GIT模型增加了两个分量，第一个分量为${E_1}$，表示当风速${v_{{\rm{w}}} }$小于临界风速$v_1^{\text{c}}$时在相对斜率$\;{\rho _1}$下的变化量；第二个分量为${E_2}$，表示当风速${v_{{\rm{w}}} }$大于临界风速$v_2^{\text{c}}$时在相对斜率$\;{\rho _2}$下的变化量，该分量采用对数形式来调整增量的变化幅度，即调整后使得风速增大引起的该分量的变化较小.

此外，对GIT模型中的风向因子和干涉因子进行简化，得到修正GIT模型的完整形式如下：

式中：常数$C$用于调整海杂波的整体幅值，该参数同$\;{\rho _1}$、$\;{\rho _2}$、$v_1^{\text{c}}$、$v_2^{\text{c}}$为修正GIT模型的5个输入参数.

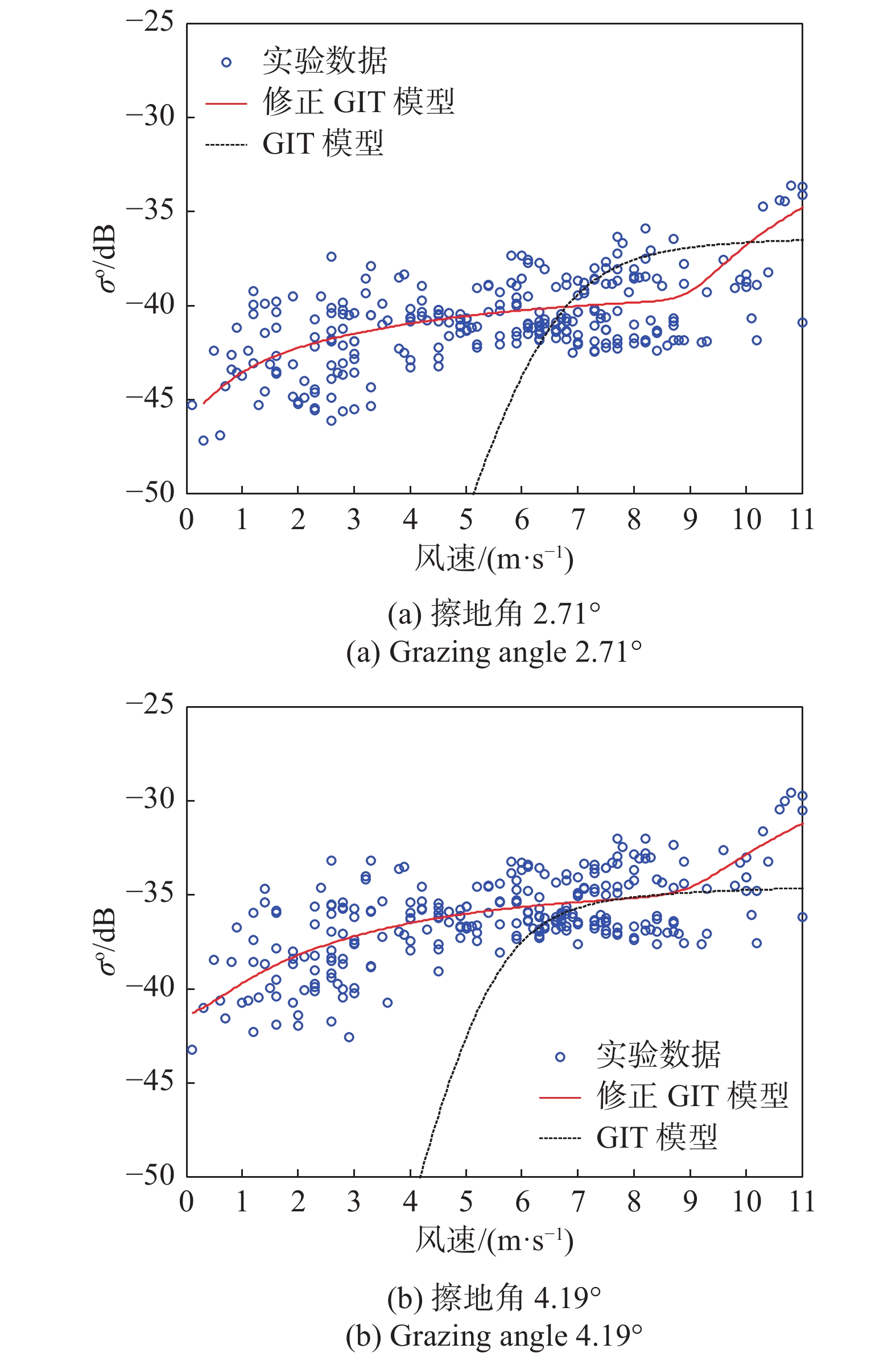
图8给出了L波段VV极化实测海杂波的修正GIT模型建模结果. 可以看出：实测数据表现出当风速大于约9 m/s时散射系数增长速率变快，在这种散射系数随风速的变化趋势建模中修正GIT模型要比GIT模型效果更好；GIT模型在高风速情况下与实测数据拟合较好，但是随风速增大散射系数增大的趋势存在拟合差异；在大约低于6 m/s风速情况下，GIT模型明显出现了散射系数的低估计，与实测数据的偏差较大.

图  8  GIT模型与修正GIT模型建模结果对比^[30]

Fig.  8  Comparison of modeling results of GIT model and modified GIT model^[30]

下载: 全尺寸图片 幻灯片

3.1.2   幅度分布建模

多年来，人们尝试了多种海杂波幅度分布模型，从早期相对简单的Rayleigh、LogNormal、Weibull分布等，到之后复杂的K分布，甚至KA分布、KK分布、WW分布等^[53]，其中的一个重要目的是拟合海杂波幅度分布的重拖尾现象^[54]. 该现象经常发生在高分辨、高海况、小擦地角等情况下，有分析认为是由较强的“海尖峰”回波导致的^[28].

多数情况下，K分布在拟合重拖尾方面具有优势. 即便如此，由于其形式复杂，实际中难以得到闭解而不便应用. 为此，有学者致力于利用实测数据建立K分布形状参数的经验模型，利于K分布的实际应用. 目前，主要有两种经验模型^{[25, 55]}，分别如下：

式中：ν为K分布的形状参数；$\phi _{{\text{gr}}}^{\text{o}}$为雷达波束照射海表面的擦地角，单位（°）；${A_{\text{c}}}$为雷达空间分辨单元的面积；${k_{{\text{pol}}}}$为一个极化修正因子（HH极化为2.09，VV极化为1.39）；${\theta _{{\text{sw}}}}$为雷达视线和涌浪浪向的夹角；$l$为雷达横向距离分辨率；$\Delta R$为径向距离分辨率；$\sigma$为视角因子(逆/顺涌时为−1/3，侧涌时为+1/3，其他方向或无涌时为0)；$k$为另一个极化修正因子（HH极化为1.7，VV极化为1.0）. 式(20)揭示了K分布的形状参数随着擦地角大小、空间分辨单元的面积、极化方式及雷达与浪向夹角的变化而变化，是空变和时变的函数. 式(21)是在式(20)的基础上进一步考虑了雷达径向距离分辨率的影响. 但两式均未考虑海况、雷达工作频率等重要因素，因此，这些模型是低精度的和不全面的.

3.1.3   多普勒谱建模

海杂波多普勒谱包括频移和展宽. 对于不同的观测时间，多普勒谱表现出不同的形状与非平稳特性. 当观测时间较长（通常大于重力波周期，秒级）时，Lee等人^[56]建立了由3个表征不同散射机制的基函数表示的模型，但形式及参数估计复杂，实际应用困难. 在此基础上，Walker等人^[26-27]利用3个高斯函数分别表征布拉格、白浪和破碎3种散射机制的谱分量，形成了一种较为简化的平均多普勒谱模型，在实际中得到广泛应用. 当观测时间较短（小于重力波周期，大于白浪和破碎散射的去相关时间）时，Miller等人^[57]建立了由两个服从伽马分布的随机变量对高斯函数形式的谱结构进行调制的短时多普勒谱模型；Ward等人^[58]借鉴复合K分布幅度建模思想，提出利用两个高斯函数对谱形状进行描述的短时多普勒谱建模方法. 但由于模型中假定海面的布拉格散射谱分量具有零多普勒频移，且白浪散射和破碎波散射共享相同的多普勒频移和展宽，因此会导致某些情况下拟合精度不高.

在实测数据的基础上，张金鹏等建立了长短时统一的时变多普勒谱模型^[36]. 该模型将3个谱分量的谱强度假设为受谱估计时间区间影响的时间随机变量，可以得到

式中：

分别为布拉格、白浪、破碎波散射谱分量的谱线形状基函数；${I_{\text{B}}}$，${I_{\text{W}}}$和${I_{\text{S}}}$分别为当谱估计时间区间为$\Delta t$情况下随时间动态变化的布拉格、白浪、破碎波散射谱分量的强度；$w_{\text{B}}^{}$，$w_{\text{W}}^{}$和$w_{\text{S}}^{}$分别为布拉格、白浪和破碎波散射分量的频谱宽度；${f_{\text{B}}}$和${f_{\text{G}}}$分别为对应于布拉格谐振波和重力波相速度的多普勒频率；$\Delta {f_{\text{s}}}$为由瞬时风和垂直重力加速度引起的在重力波相速度基础上的附加速度频移量，当重力波相速度频移量${f_{\text{G}}}$为正时，$\Delta {f_{\text{s}}}$前的符号取正，反之相反. $\pm$在物理意义上表征附加速度是沿着重力波相速度方向的.

值得注意的是，该时变多普勒谱模型中，3个谱分量的强度之和${I_{\text{B}}} + {I_{\text{W}}} + {I_{\text{S}}}$符合K分布中的调制分量$\Gamma$分布. 在对时变多普勒谱进行参数优化时，需附加约束条件

此条件可以保证破碎波和白浪散射的多普勒频移（主要来自于重力波相速度）大于布拉格散射的谱频移，与物理机理是相符的.

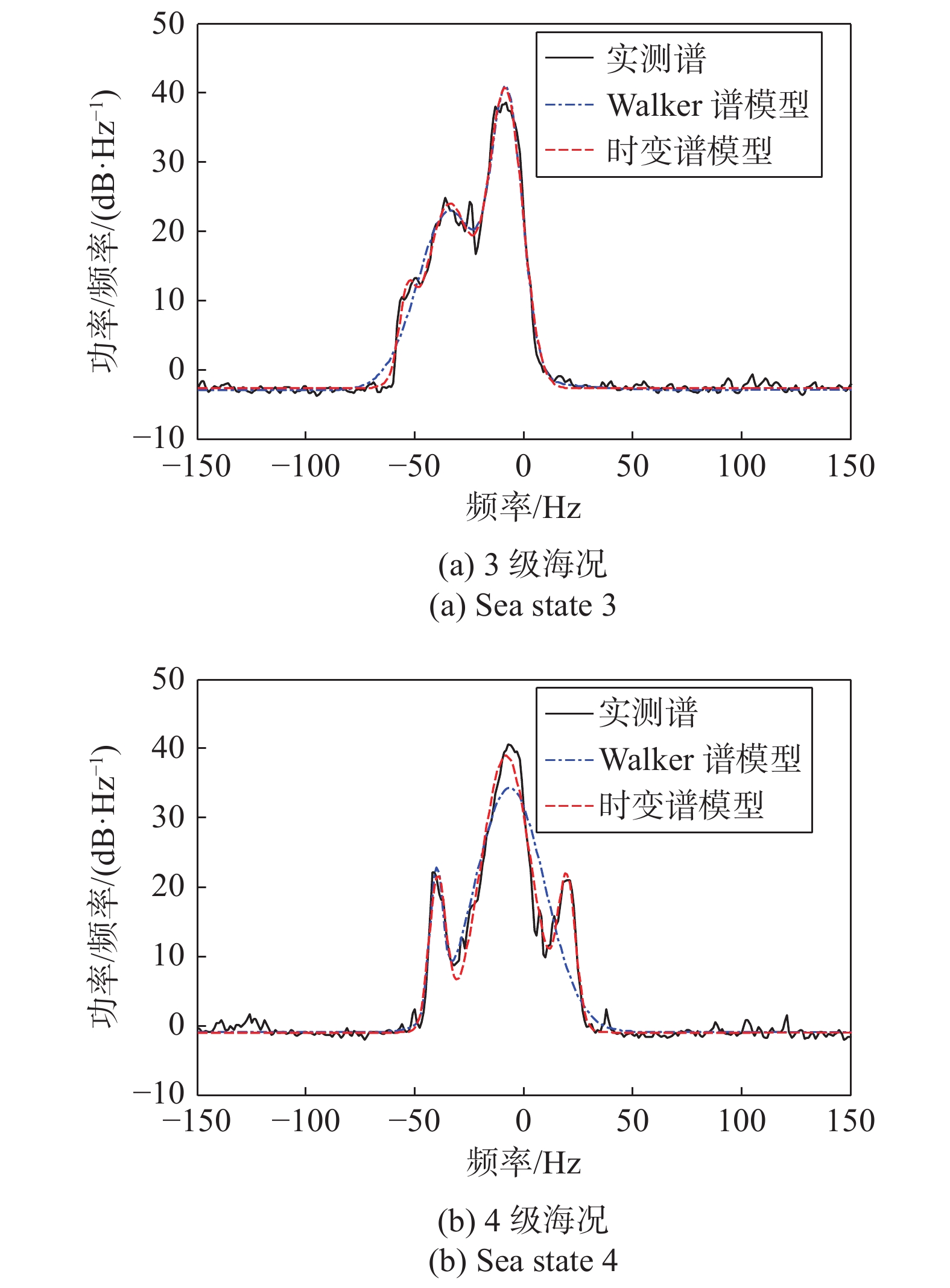
图9给出了岸基UHF波段海杂波数据平均多普勒谱的建模效果. 可以看出，3级海况下，UHF波段平均谱具有两个明显的谱峰，且在−50 Hz左右具有一个较弱的类似谱峰的突起，时变谱模型刻画出了该细微结构，而Walker谱模型忽略了该结构. 在4级海况下，UHF波段海杂波平均谱表现出3个明显的谱峰，说明较高海况下海浪的速度分量更为复杂. 在该情况下，时变谱模型可以实现整个谱形状（3个谱峰）的准确建模，而Walker模型忽略掉了正频移上的谱峰，且对中心谱峰强度的描述也存在明显偏差.

图  9  岸基UHF波段海杂波平均多普勒谱建模效果

Fig.  9  The modelled average Doppler spectrum of UHF-band sea clutter

下载: 全尺寸图片 幻灯片

3.2   深度学习建模

随着海量海杂波和环境参数实测数据的累积，探究海杂波特性与影响要素之间隐含的复杂多参数、非线性映射关系，依靠传统的基于统计的经验建模方法已难以实施，尝试利用基于深度学习的机器建模方法似乎更为合适.

目前，中国电波传播研究所搭建起了基于深度学习的海杂波建模网络平台，形成了多参数、非线性海杂波建模能力^[45]. 深度学习海杂波建模方法涉及的重点问题如下：

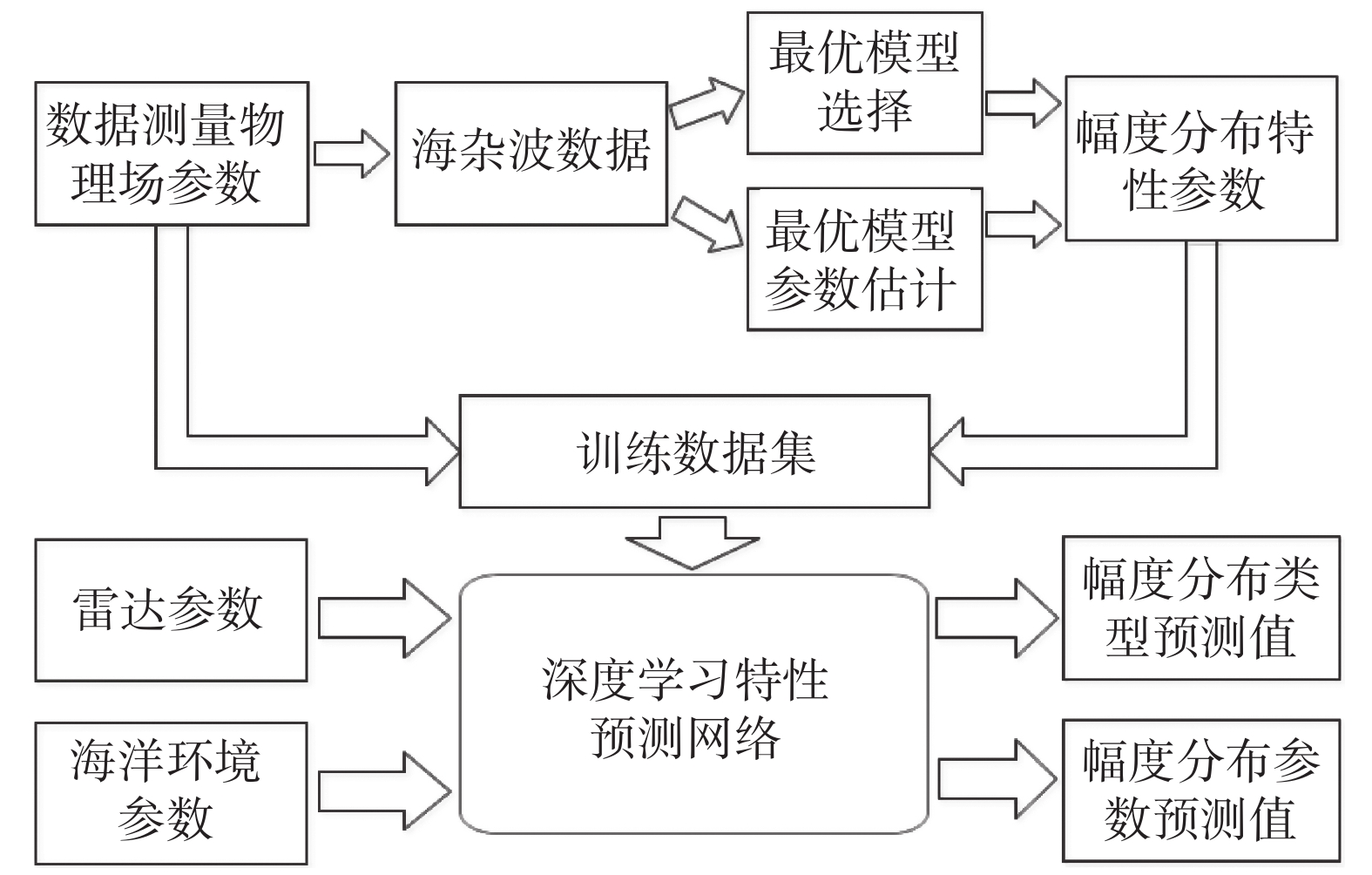
① 海杂波特性数据集的构建. 规范化的海杂波特性数据集是实现海杂波深度学习建模的基础，该数据集除包括海杂波特性参数样本外，还须要具备同时同地测量的海浪、气象、平台、雷达等参数数据，以此作为深度学习模型的输入信息. 海杂波特性参量来源于海杂波原始测量数据提取得到的多维特性参数，包括散射系数、幅度分布类型、分布形状参数、尺度参数、多普勒谱频移、展宽等，以此作为深度学习模型的输出信息.

由于海杂波测量条件物理场参数众多，数量级不同，量纲不同，在开展深度学习训练之前，采用Z-Score标准化方法对海杂波测量条件物理场参数进行标准化，即

式中：$Y$为标准化后的参数值，无量纲，均值为0，方差为1；$X$为每个物理场参数；$\bar X$为参数均值；$\sigma$为参数标准差.

② 损失函数的建立. 针对不同的海杂波特性参量建模问题，须建立不同的损失函数用于网络模型的训练优化. 对于散射系数，可使用最小二乘损失函数；对于幅度分布，由于同时涉及分布的类型和参数，因此须将建模问题视为一个分类问题和回归问题之和，将海杂波幅度分布类型的分类预测损失和分布参数的回归损失联合起来，通过超参数加权建立一体化损失函数；对于多普勒谱频移和展宽建模而言，实质上是两个参数的联合回归问题，因此通常采用两个最小二乘损失项加权的方式，建立联合损失函数.

③ 深度学习网络架构和参数的确定. 针对不同的海杂波特性建模问题，选取并建立不同的深度学习网络模型架构，如全连接网络、卷积神经网络、循环神经网络等，设计模型多层适用性评价准则，选择合适的深度学习模型参数配置方案，包括隐含层数、神经元数等.

④ 网络模型的验证与优化. 基于新的海杂波数据样本，对海杂波特性建模网络进行测试和优化，根据测试误差结果，调节网络模型宽度、模型深度等模型结构以及模型超参数，不断优化模型中的权值参数，最终形成具有较高泛化性能的海杂波模型.

下面以岸基S波段（数据集包含训练数据样本208160个）为例，讨论海杂波深度学习建模结果.

3.2.1   散射系数建模

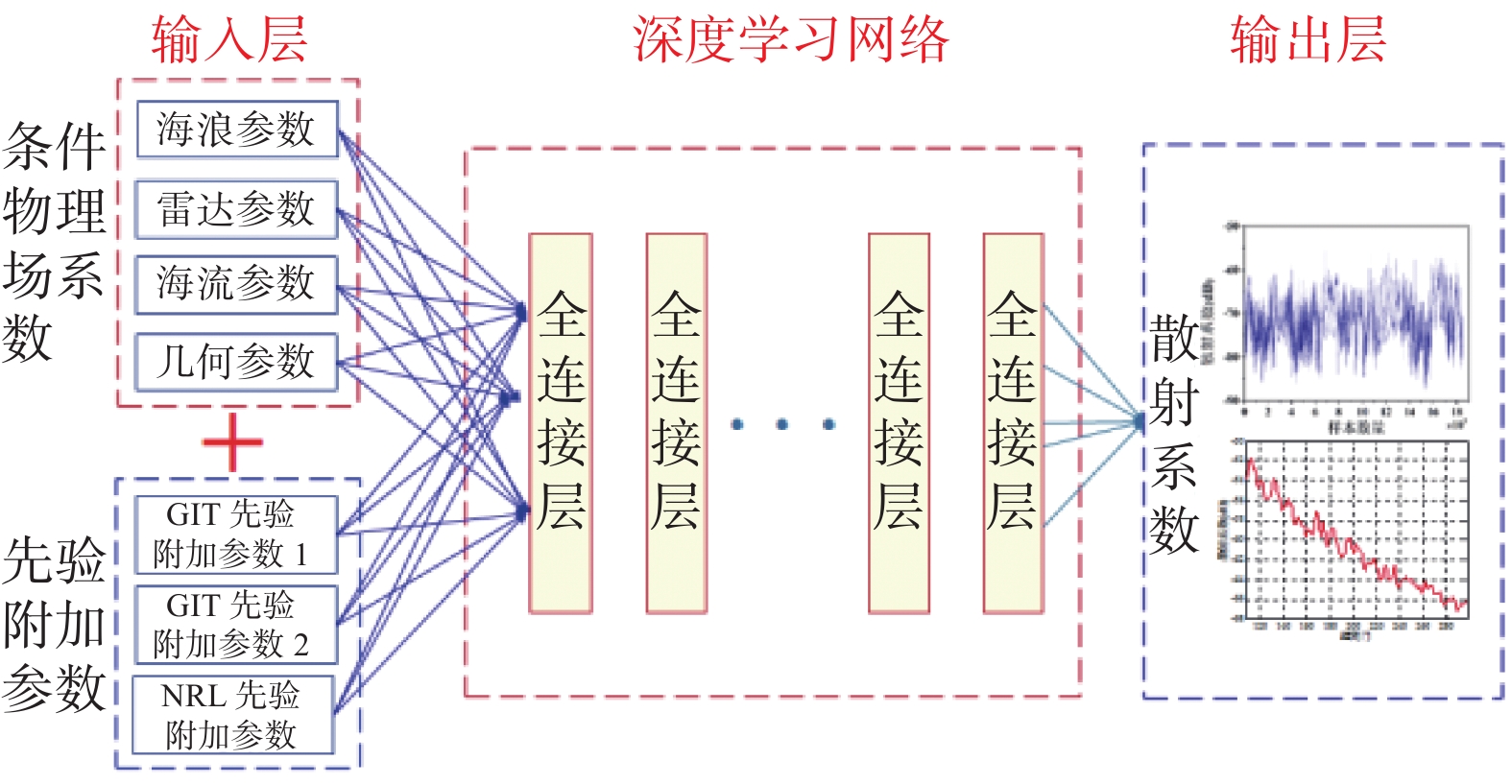
图10给出了散射系数深度学习模型架构，以影响散射系数的海洋物理场、雷达等参数作为基础输入，以经验的GIT模型和NRL模型中主要用于描述擦地角、浪高、浪向和海况影响规律的非线性函数为先验附加输入，合计14个输入参数（见表4）共同实现散射系数的训练建模. 其中GIT模型中的非线性函数采用描述擦地角和平均浪高影响规律的干涉因子（$p_{{\text{GIT1}}}^{}$），以及描述浪向角影响规律的浪向因子（$p_{{\text{GIT2}}}^{}$），具体如下：

式中：${\sigma _\phi } = (14.4\lambda + 5.5){\phi _{{\text{gr}}}}{H_{{\text{av}}}}/\lambda$；${\phi _{{\text{gr}}}}$为擦地角，单位（°）；${H_{{\text{av}}}}$为平均浪高，单位m.

式中，${\theta _{\text{w}}}$为浪向与雷达视线的夹角，单位rad.

NRL模型中的非线性函数主要采用描述海况影响规律的非线性项（$p_{{\text{NRL}}}^{}$），具体表达式为

式中，SS为道格拉斯海况.

以上这些经验模型的相关非线性函数作为深度学习网络的先验信息，可有效降低神经网络所要学习函数的非线性程度，有助于提高网络对海杂波特性预测认知的准确率.

图  10  海杂波散射系数深度学习模型架构

Fig.  10  Architecture of the deep learning model of the sea clutter scattering coefficient

下载: 全尺寸图片 幻灯片

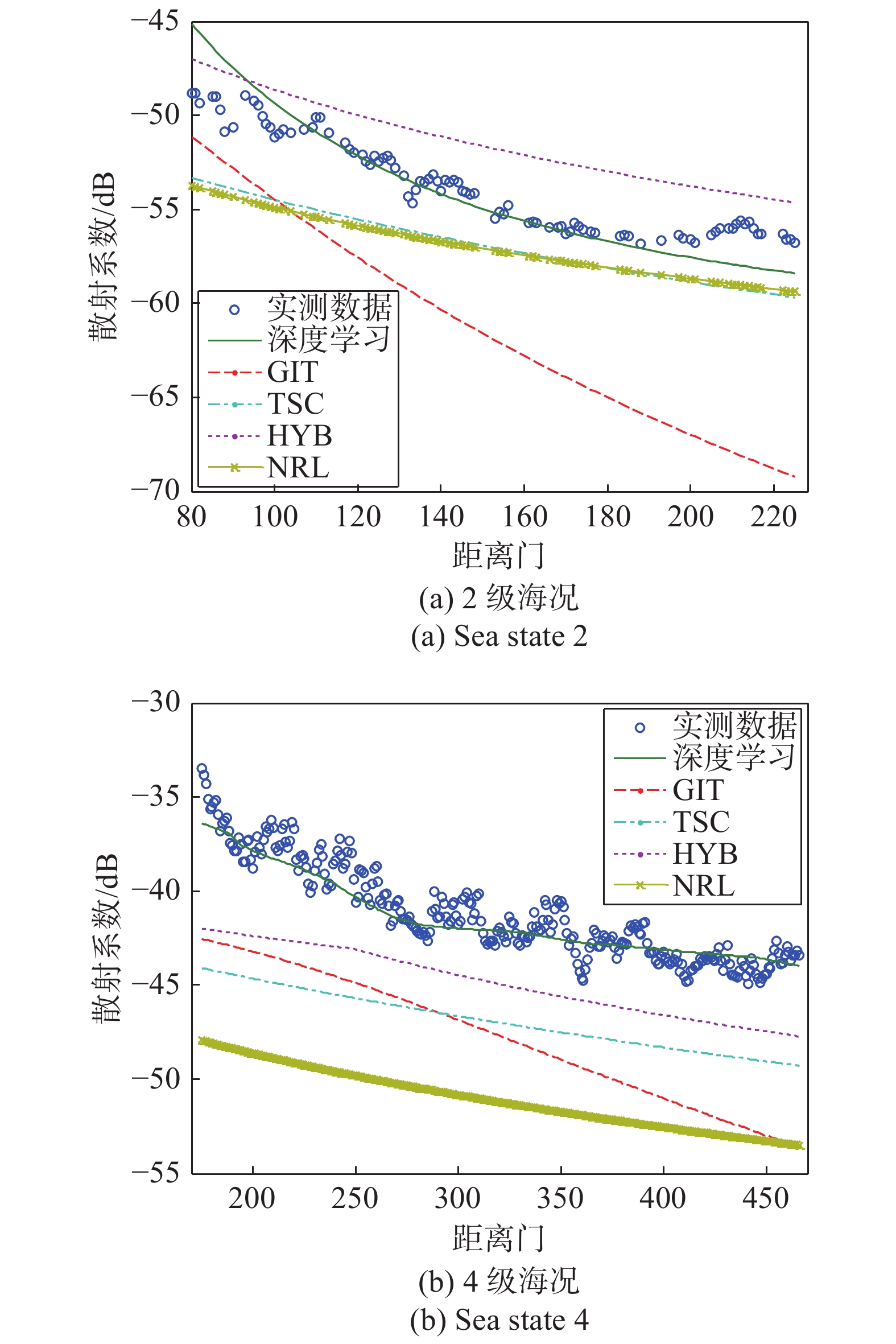
表  4  海杂波幅度均值认知模型输入参数

Tab.  4  The input parameters of the cognitive model of sea clutter mean amplitude

参数类型	序号	参数名称	符号	单位
海浪参数	1	有效浪高	${H_{{\text{sig}}}}$	m
	2	最大浪高	${H_{\max }}$	m
	3	平均浪高	${H_{{\text{av}}}}$	m
	4	浪向角	${\theta _{\rm{w}}}$	（°）
	5	浪向扩展角	$\theta _{\rm{w}}^{ {\text{spread} } }$	（°）
	6	平均浪周期	${T_{{\text{av}}}}$	s
	7	最大浪周期	${T_{\max }}$	s
海流参数	8	流速	${v_{\text{c}}}$	m/s
	9	流向角	${\theta _{\text{c}}}$	（°）
雷达和平台参数	10	距离分辨率	${d_{\text{R}}}$	m
	11	擦地角	${\phi _{{\text{gr}}}}$	（°）
经验模型先验附加参数	12	GIT先验参数1	$p_{{\text{GIT1}}}^{}$	-
	13	GIT先验参数2	$p_{{\text{GIT2}}}^{}$	-
	14	NRL先验参数	$p_{{\text{NRL}}}^{}$	-

下载: 导出CSV 

| 显示表格

经过均衡训练速度和建模精度，采用了含8个隐层的全连接神经网络，每层的神经元个数分别为512、512、256、256、128、128、64、64，学习率设置为0.001，图11给出了2组典型的散射系数建模结果. 可以看出，深度学习建模结果与实测数据吻合得最佳，均优于其他4种经验模型. 对所有208160个海杂波样本数据的建模误差定量分析，散射系数建模平均误差为1.84 dB.

图  11  海杂波散射系数建模结果对比

Fig.  11  Comparison of modeling results of sea clutter scattering coefficient

下载: 全尺寸图片 幻灯片

3.2.2   幅度分布建模

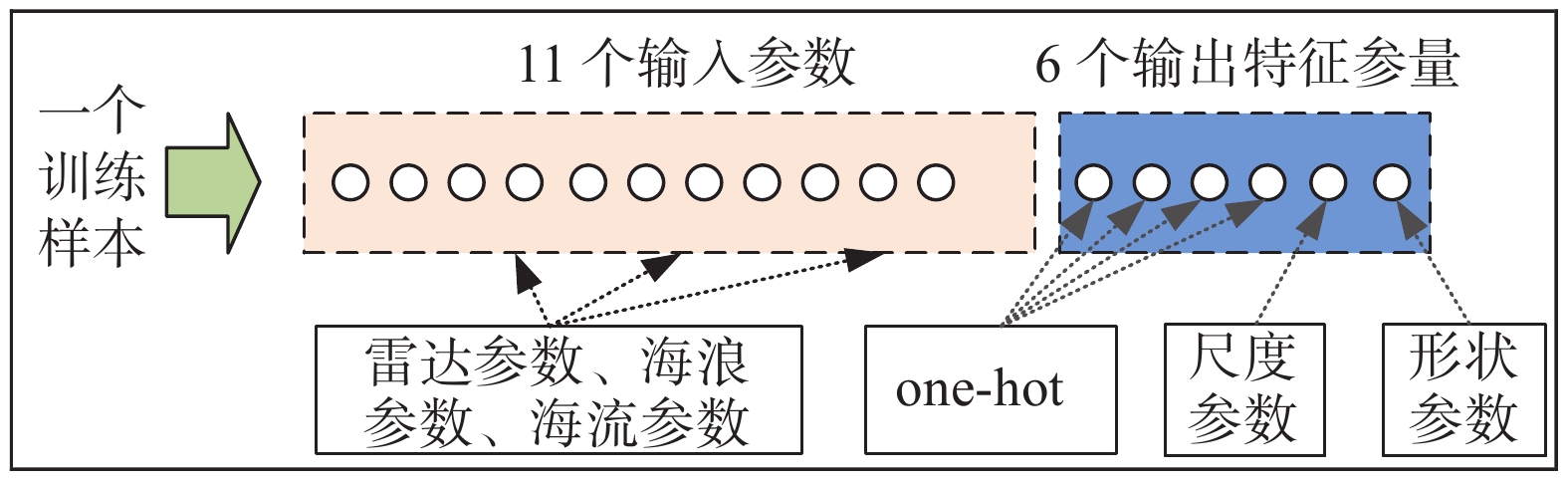
图12给出了幅度分布深度学习模型架构，以海杂波探测场景中各类物理场参数为输入，以海杂波数据的幅度分布类型和分布参数为联合输出. 输入参数包括擦地角、雷达分辨率，以及表4中前9个海洋环境参数，经标准化处理后形成共计11个输入参数. 幅度分布类型设定为Rayleigh、LogNormal、Weibull和K等4种分布，在深度学习网络输出样本中用one-hot编码来表示，即Label为一个4维的向量，只有1个值为1，其余为0. 为规范深度学习网络的输出层变量，统一用尺度参数和形状参数两个参数作为输出变量，即Rayleigh分布参数b和Lognormal分布的均值参数都命名为“尺度参数”，Lognormal分布的方差参数命名为“形状参数”. 根据这些对输入和输出样本的处理，幅度分布建模的训练样本数据结构可表示为如图13所示的形式.

图  12  海杂波幅度分布深度学习建模框架

Fig.  12  Flow chart of the deep learning modeling process of sea clutter amplitude distribution

下载: 全尺寸图片 幻灯片

图  13  训练样本数据结构

Fig.  13  Training sample data structure

下载: 全尺寸图片 幻灯片

将幅度分布类型的分类损失和分布参数的回归损失联合起来，通过超参数加权，构成统一的预测损失函数，可表示为

式中：${L_1}\left( {p|p'} \right)$为幅度分布类型的分类损失；${L_2}\left( {b|b'} \right)$和${L_3}\left( {v|v'} \right)$分别为分布尺度参数和形状参数的回归损失；${\lambda _1}$，${\lambda _2}$，${\lambda _3}$为对应各项损失的权重超参数，用于控制各项损失对总体损失函数的贡献程度.

分类损失可以用softmax交叉熵损失来计算，该损失通常用于判断模型对真实概率分布估计的准确程度，计算公式为

式中：i代表类型编号；$p'$为真实的概率分布（即Label的one-hot编码）；$p$为预测的概率分布. 尺度参数和形状参数的回归损失用最小二乘误差表示.

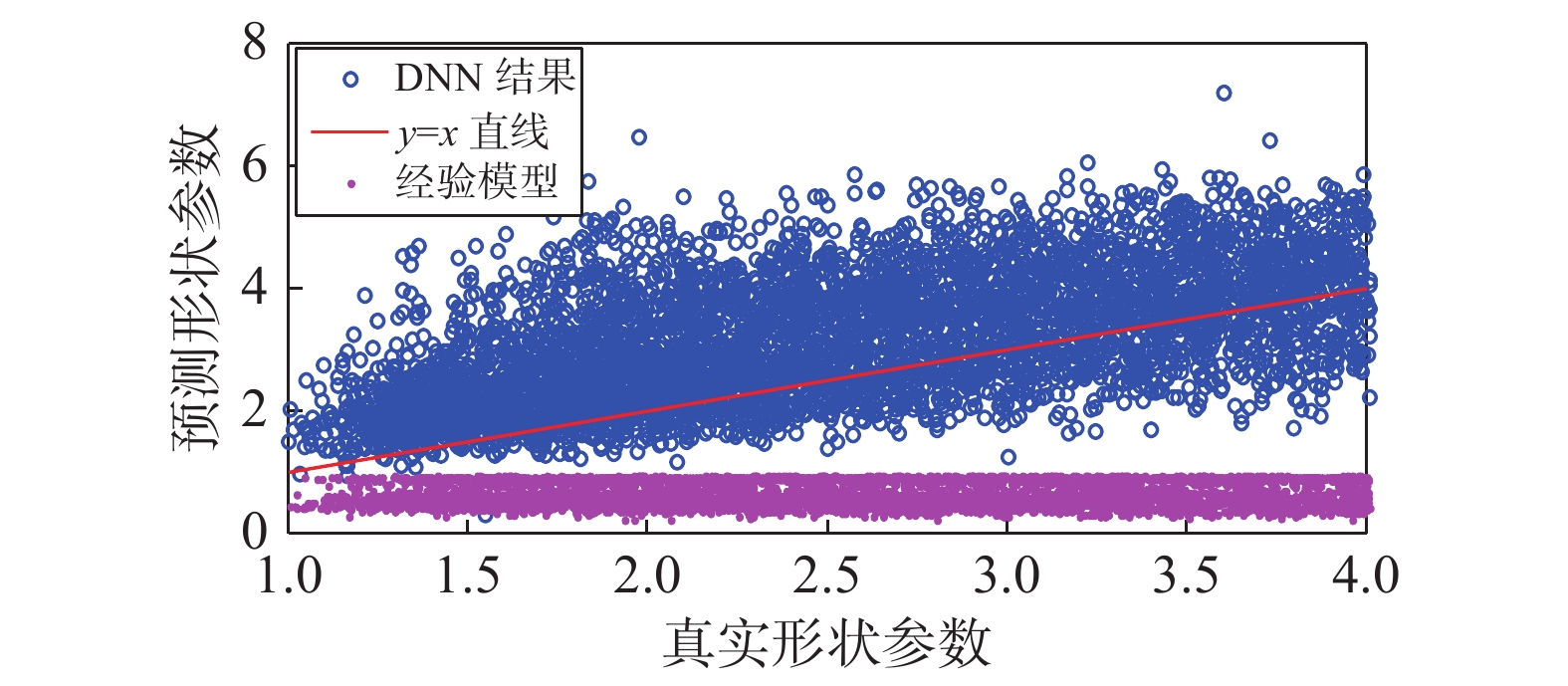
经过多次实验均衡了性能与精度之后，最终采用2个隐含层结构，且每个隐含层分别取64、32个神经元，学习率为0.001. 从训练数据集中选取8723组K分布数据，图14给出了K分布形状参数建模结果对比. 可以看出，尽管其与y=x线仍存在一定偏离度，但DNN模型预测的形状参数与真实形状参数吻合较好，而经验模型的建模结果严重偏离y=x线，说明DNN建模结果远优于经验模型.

图  14  海杂波K分布形状参数建模结果对比

Fig.  14  Comparison of modeling results of K-distribution shape parameters of sea clutter

下载: 全尺寸图片 幻灯片

3.2.3   多普勒谱建模

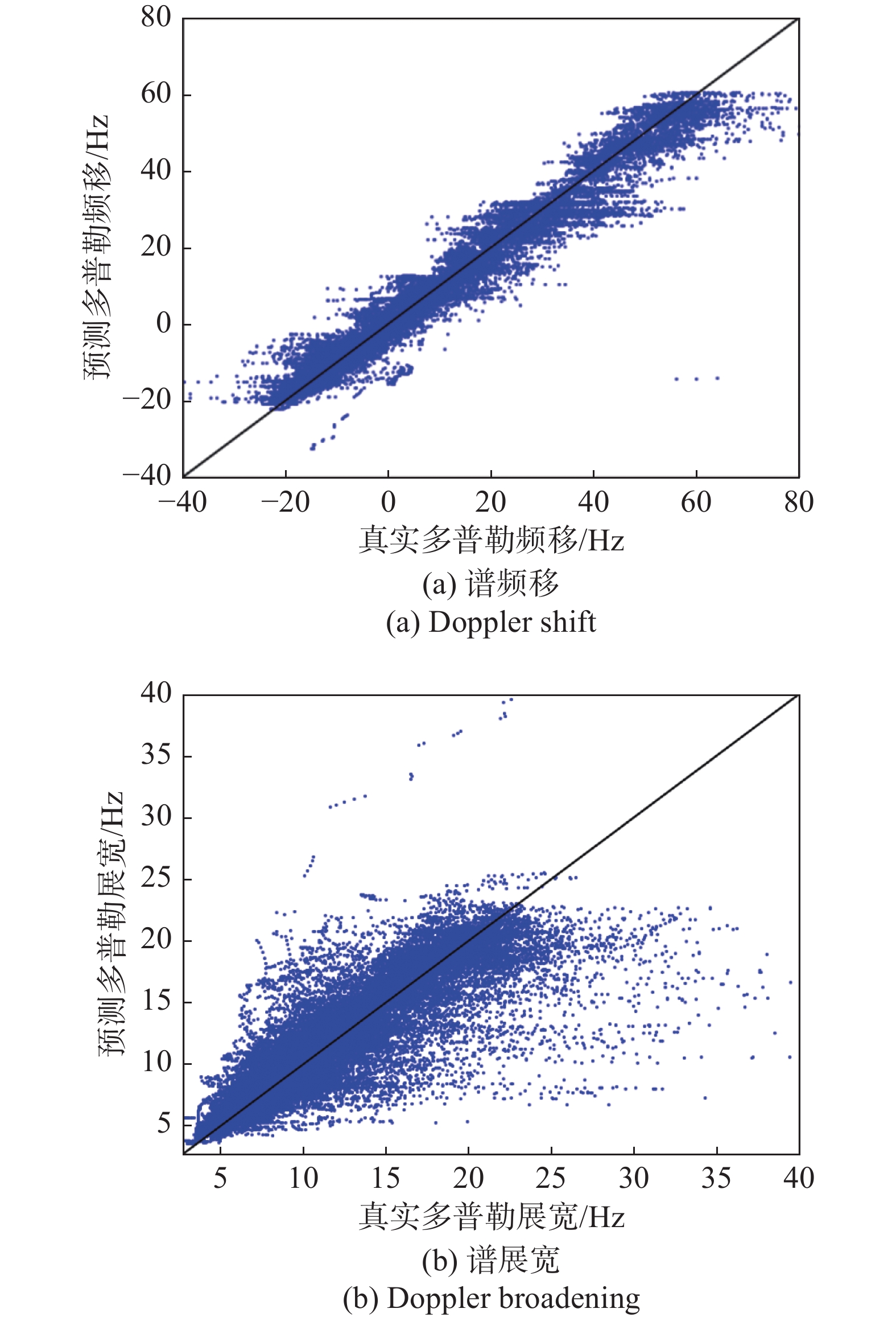
实践发现，全连接网络更适合海杂波多普勒谱建模^[59]. 表5给出了海杂波谱参数的全连接网络模型架构，模型的输入数据与幅度分布建模输入参数一致，共计11个参数. 模型的输出数据为多普勒谱频移和展宽. 使用Flatten函数，可将多维的输入数据转换成一维数据. 在全连接层的每一层操作后均添加batch_normalization和Rule激活函数，以加快神经网络的收敛和缓解过拟合. 训练过程中，设定初始学习率为0.01，每200个epoch进行一次学习率衰减，衰减为原来的0.1. 图15给出了海杂波多普勒谱建模结果. 横坐标表示实测的多普勒频移或展宽，纵坐标表示模型预测的多普勒频移或展宽，图中的样本点越接近y=x线，说明模型预测越准确，越接近真实值. 从图15可以看出，深度学习模型较为准确地实现了海杂波谱频移和展宽建模，就图中所给数据而言，频移均方根误差为4.01 Hz，谱展宽均方根误差为2.76 Hz.

表  5  海杂波谱深度神经网络模型架构

Tab.  5  Deep neural network model architecture of sea clutter doppler spectrum

网络层（Layer (type)）	输出维度Output Shape
flatten_1 (Flatten) dense_1 (Dense) batch_normalization_1 leaky_re_lu_1 (LeakyReLU) dense_2 (Dense) batch_normalization_2 leaky_re_lu_2 (LeakyReLU) dense_3 (Dense) batch_normalization_3 leaky_re_lu_3 (LeakyReLU) dense_4 (Dense) batch_normalization_4 leaky_re_lu_4 (LeakyReLU) dense_5 (Dense) batch_normalization_5 leaky_re_lu_5 (LeakyReLU) dense_6 (Dense)	(None, 15) (None, 32) (None, 32) (None, 32) (None, 64) (None, 64) (None, 64) (None, 64) (None, 64) (None, 64) (None, 32) (None, 32) (None, 32) (None, 16) (None, 16) (None, 16) (None, 2)

下载: 导出CSV 

| 显示表格

图  15  海杂波多普勒谱建模结果

Fig.  15  Doppler modeling results of sea clutter

下载: 全尺寸图片 幻灯片

4   研究展望

海杂波与海洋地质、海洋水文、海洋气象、雷达体制与参数、平台参数等多种因素密切相关，决定了对海杂波特性认知的困难性和长期性，正如《雷达手册》第3版^[60]所述“海杂波理论问题仍悬而未决. 最通用的模型实际上是一些以偶然的事实为基础的假设组合，并且模型为什么能用尚无明确的理由.” 还需关注的是，在第2版到第3版之间的近20年间，海杂波理论研究未见显著进展.

海杂波测量是实现海杂波特性认知的重要手段. 当前，海杂波测量主要侧重于雷达主动和单站测量，双站（多站）和被动测量较少，难以满足多基地雷达、组网雷达和被动雷达发展需求. 因此，双站和被动测量必将成为今后海杂波测量技术的发展重点.

正如文中所述，深度学习为海杂波特性精确建模带来了新的途径. 但是，不管是基于参数化的经验建模或是非参数化的深度学习建模，所需要的输入参数多且不统一，对雷达应用造成困难. 如何使输入参数少而精且实际中易获取，是今后海杂波特性建模方法研究努力的方向.

就雷达应用场景而言，海杂波测量与建模还有未涉猎或须深化研究的方面，如陆海交界区域的海杂波特性、海面有污染物时的海杂波特性、海上反常传播（如大气波导）条件下的海杂波特性等. 目前，这些方面不但缺乏实测数据，理论研究也较少.

基于电磁散射理论的海杂波理论研究，虽然与实际应用存在较大差距，但仍对海杂波形成机理和某些现象的解释起到至关重要的作用^[61-62]. 在及时吸收海洋界对海谱模型研究进展的同时，今后在动态多尺度、大场景的海杂波电磁散射模拟计算方法方面需要有新的突破，为逐步逼近真实海杂波特性奠定方法基础.