0   引　言

电离层电场和等离子体漂移对研究电离层形态有着重要的作用^[1-2]，对它们的研究是揭示众多重要电离层现象物理成因的关键问题的手段之一^[3]。近些年来众多学者^[4-12]对电离层等离子体漂移测量技术和运动特性进行了大量的研究，国外B.W Reinisch等^[4-5]提出利用干涉仪技术对等离子体进行漂移测量，给出了利用数字测高仪漂移分析（digisonde drift analysis, DDA）计算漂移速度的方法；Kouba D等^[8-10]利用加拿大数字探测仪（Canadian Advanced Digital Ionosonde, CADI）和数字测高仪DPS-4D对中纬地区等离子体回波信号进行漂移测量，分别针对F层和E层从高度范围、多普勒频率限制和天顶角约束等三方面分析了等离子体回波点的选取原则。国内万卫星等^[11]利用数字测高仪中的漂移测量研究小尺度的电离层扰动，有效提取了大尺度电离层扰动的传播参量；鲁转侠等^[12]验证了时间内插技术在电离层探测频率增加的同时能够有效缩短探测时间；蔚娜等^[13]构建了运动着的电离层不均匀体的理论模型，估计了电离层不均匀体的运动速度；宋磊等^[14]利用单台电离层测高仪测量电离层不均匀体水平尺度，理论推导了电离层不均匀体水平尺度的基本方法，并利用国外观测站的数据进行了验证；王霄^[15]利用海南电离层观测站安装的DPS-4D电离层测高仪数据给出了海南地区电离层漂移的日变化、季节变化及其可能的年变化等特征。

DPS-4D电离层测高仪采用干涉仪测向体制实现等离子体漂移测量，其利用回波中较强峰值点在各阵元之间的幅度/相位差异特征信息，通过与预先计算好的方向-特征信息表做对比得到回波的方向信息。此方法优点是计算量小，且由于其仅需要通过查表即可获取回波点方向信息，系统配置发生变更时，查表运算部分无需改变，仅升级方向-特征信息表即可实现系统更新。但在实际系统部署过程中，通常会受到现场条件的约束，例如周边植被、高程落差、天馈性能不一致等多种因素，均会对到达回波的阵列接收产生一定影响，而常规的查表技术路线对这些影响因素不具有提升的能力。同时由于常规干涉仪方法仅利用了回波峰值点附带的方向信息，相当于在信号能量域进行了预选，损失了一部分非峰值且附带强空间信息的回波能量，再加上同时用干涉仪测向存在相位模糊问题^[16]，从而降低了测向精度。

本文改进了电离层等离子体回波的测量方法，通过采用时间内插技术提升定频探测频率个数缩短探测时间、采用干扰避让技术去除受干扰影响的回波散射源、采用波束合成方法对回波散射源进行测向，有效提升了回波散射源方向测量的稳健性和等离子体运动速度的稳定性，并与海南富克站部署的DPS-4D电离层测高仪测量结果比较，验证了本文所述方法的先进性。

1   电离层等离子体漂移测量方法

1.1   电离层等离子体回波测向

电离层测高仪垂直向上发射高频电磁波脉冲信号，由于发射天线具有一定的波束宽度，发射脉冲会“照亮”一大块区域的电离层等离子体（通常直径有几百千米，与发射天线的波束宽度以及等离子体的高度有关），当入射电磁波频率达到电离层各个反射平面的截止频率时就会在等离子体密度等值面的各点发生反射，当反射面正对地面接收点时，其回波就能被地面接收系统接收。利用四副有源正交环组成的天线阵（边长为60 m的正三角形阵列）接收电离层等离子体回波信号，对回波的多普勒信息进行检测，提取有效回波散射源，通过对回波散射源进行测向获取等离子体在空间的位置。

采用数字波束合成(digital beam-forming，DBF)技术实现波达方向(direction of arrival，DOA)估计。对阵列各单元信号加权求和，即用导向矢量$\boldsymbol{W}$与阵列信号$\boldsymbol{X}\left(t\right)$作内积，则波束合成后的信号表达式为

用导向矢量$\boldsymbol{W}$的相位对阵列信号各分量进行相位补偿，使得在期望信号方向上各个分量同相相加，以形成天线方向图的主瓣。而在其他方向上，非同相相加形成天线方向图的副瓣。天线的方位角范围为$-18{0}{\text{°}}\sim 18{0}{\text{°}}$，天顶角范围为$0\sim 9{0}{\text{°}}$，对方位角和天顶角分别以1°为步进进行波束合成，对所有波束合成信号在方位角和天顶角范围内进行二维峰值搜索，最大峰值信号对应的方位角和天顶角即为信号实际来波方向，该测向方法准确率高，有效避免了干涉仪测向法存在的相位模糊问题。

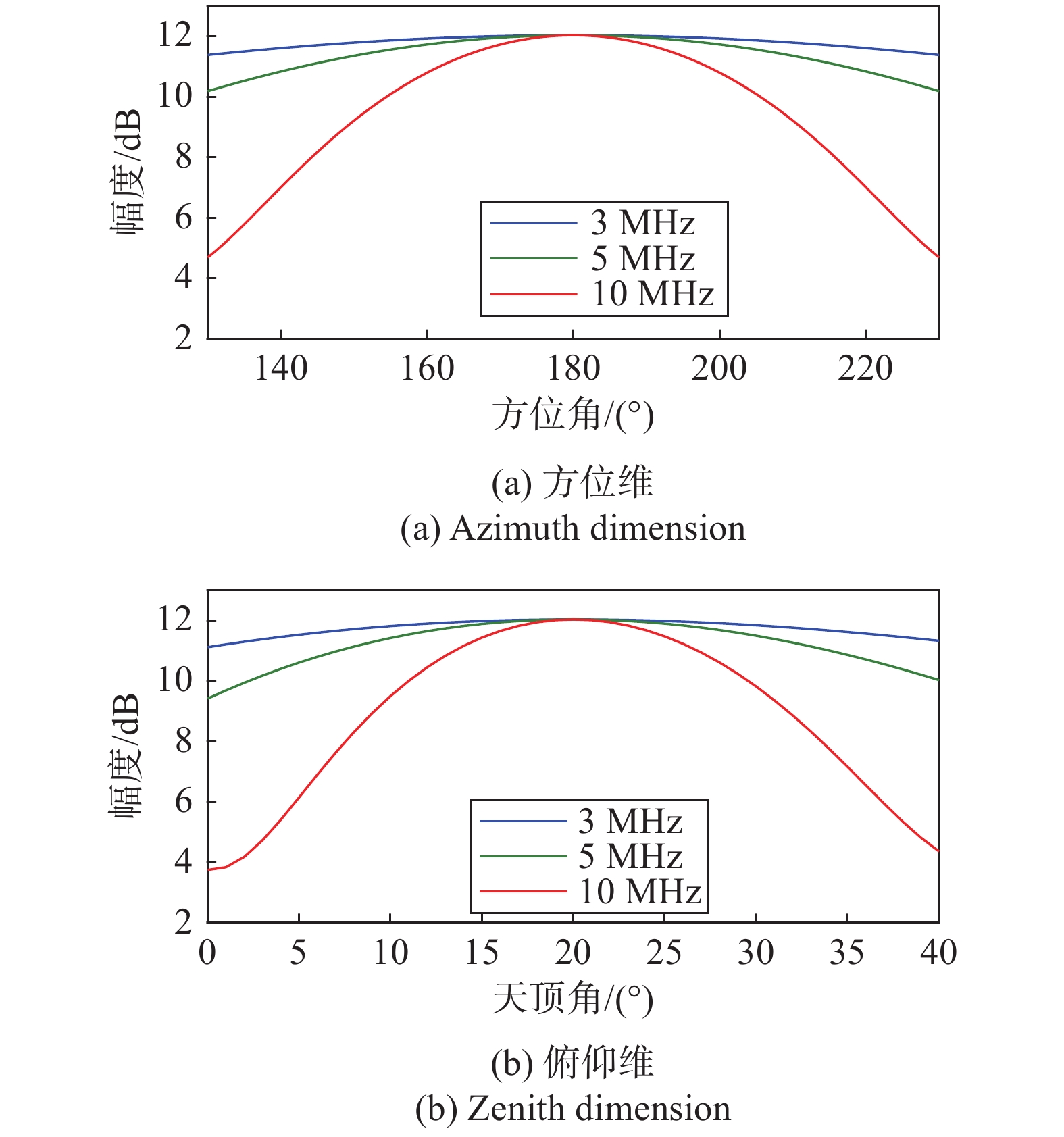
由于本系统的关注范围为顶空区域（顶空角约40°以内），结合三顶点一中心的布阵方式，阵列孔径在顶空区域变化梯度较为平缓，也降低了波束方向图的各向异性，因此在波束合成方向图上能够保持较好的对称分布特性。图1给出了指向方位角180°、天顶角20°的三个典型频率（3 MHz、5 MHz、10 MHz）条件下的阵列波束合成方向图。

图  1  波束合成方向图(方位角180°、天顶角20°)

Fig.  1  Beamforming pattern (azimuth 180°, zenith 20°)

下载: 全尺寸图片 幻灯片

1.2   工作参数确定

根据电离层实时状态选取漂移测量探测频率，该频率应保证电离层等离子体回波来自于指定的电离层。以F层为例，首先扫频探测形成垂测电离图，然后利用垂测电离图判读算法^[17]得到F₂层最小可用频率${f}_{\mathrm{m}\mathrm{i}\mathrm{n}}{\mathrm{F}}_{2}$和${\mathrm{F}}_{2}$层临界频率${f}_{\mathrm{o}}{\mathrm{F}}_{2}$，最后根据公式（2）确定漂移测量的起始频率${f}_{\mathrm{s}}$：

探测频率通常在400 kHz频段内选择，本文方法以20 kHz为步进选取20个频率，相比DPS-4D采用50 kHz步进共计8个频率的方法，频率数增加了1.5倍，可以有效改善等离子体回波点数。

为了解决频率数增多带来的探测时间变长的问题，采用时间内插方式缩短系统探测时间，如图2所示。

所谓时间内插是指在每个频率的脉冲重复周期间插入多个频率进行探测，图2中20个探测频率为一次循环，20个频率探测完成后进行下一次循环探测，脉冲重复周期为6.4 ms，每个频点周期为128 ms，对应多普勒范围为−3.9~3.9 Hz，每个频点发射128个脉冲，积累时间为16.384 s，多普勒分辨率为0.061 Hz，可有效提升多普勒分辨率的同时缩短探测时间。

图  2  时间内插示意图

Fig.  2  Time interpolation diagram

下载: 全尺寸图片 幻灯片

1.3   有效回波信号确定

1.3.1   干扰避让

等离子体回波信号不可避免地会受到外部短波信号的干扰，影响测向结果的准确性。本文采用干扰避让技术，即对多普勒谱图进行干扰检测，如果检测到多普勒谱图中存在干扰，则该频点的等离子体回波信号不参与测向运算。

多普勒谱图中主要存在两种形式的干扰：一种是同频干扰，特点是占据所有的高度单元，该干扰通过设置门限值来检测，若所有高度单元上的回波能量均大于该门限值，则判定为同频干扰；另一种是“条状”干扰，特点是在多普勒域与高度域上等间隔出现. 针对条状干扰的判别准则如下：

1)在多普勒域上进行峰值检测，计算峰值点的 多普勒频率，判断其是否均匀分布；

2)在高度域上设定一个门限值，计算高于门限值的信号占据的高度单元数，判断其是否均匀分布。

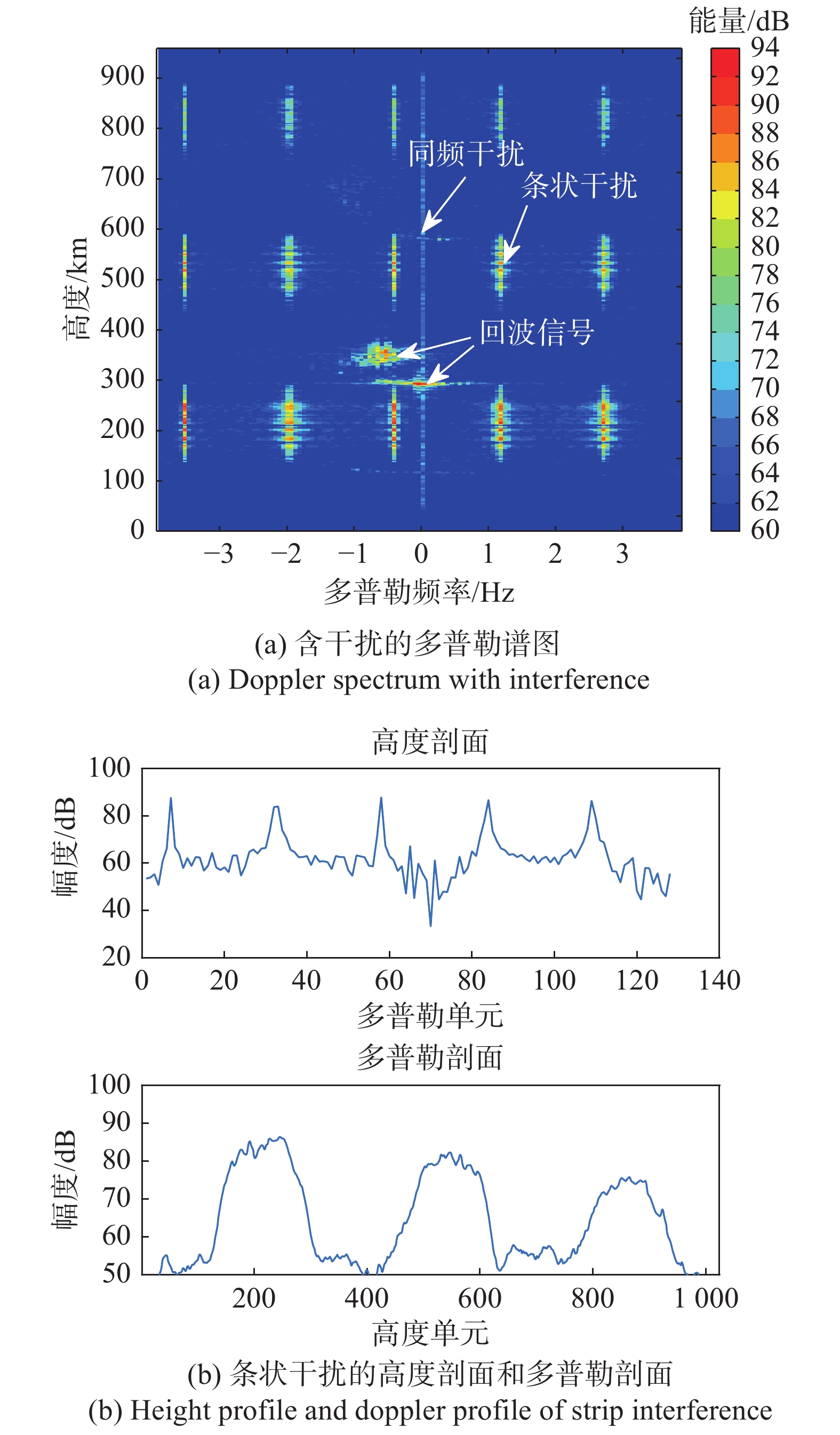
图3(a)给出了掺杂干扰的回波信号多普勒谱图，图3(b)给出了条状干扰的高度剖面（第256个高度单元处，对应高度240 km）和多普勒剖面（第6个多普勒单元处，对应多普勒频率−3.54 Hz）。图3(b)高度剖面中，峰值点处的多普勒单元序号依次为6、32、58、84、110，在多普勒域中呈均匀分布；在多普勒剖面中，3个高度包络中心点分别位于第210、530、850高度单元处，每个包络约占据180个高度单元，在高度域中呈均匀分布。该干扰符合条状干扰的判别准则，将不进行后续的散射源测向处理。

图  3  带干扰的多普勒谱图及条状干扰剖面

Fig.  3  Doppler spectrogram with interference and its section

下载: 全尺寸图片 幻灯片

1.3.2   有效信号的确定原则

准确确定电离层等离子体回波信号所在的反射虚高，是漂移速度计算的基础。本文通过多普勒域能量曲线来确定高度范围，多普勒域能量曲线即多普勒域回波信号能量${{A_{{f_{{\text{d}}i}}}}}$向高度轴的投影，按公式(3)计算：

式中：${A_{\text{h}}}$为高度单元h对应的多普勒域信号幅度累加值；N为多普勒单元数.

根据电离层不同层所在高度范围来约束信号的检测区间，如E层的高度范围为80~120 km、F层的高度范围为200~600 km；在高度区间内滑窗处理得到能量最大点，取最大能量点左右各10 km，即20 km作为有效回波的高度范围。

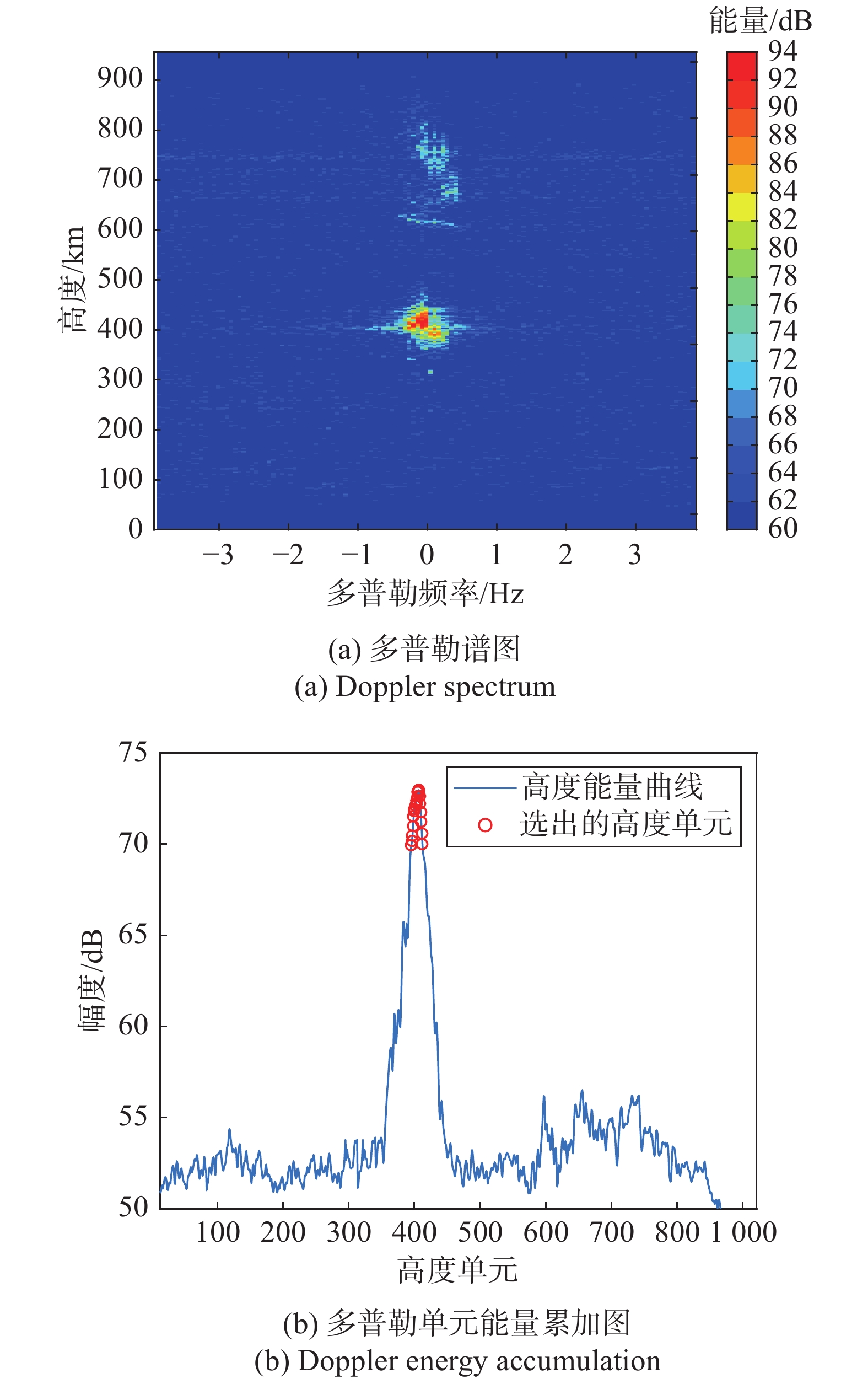
图4(a)给出了某频率的多普勒谱图，图4(b)给出了相应的多普勒域能量曲线及选取的回波高度单元。本文数据采样率为160 kHz，考虑双程传播，其高度单元间隔为0.9375 km，选取21个高度单元，相较于DPS-4D选取8个高度单元，其高度单元间隔为2.5 km的处理，可以增加检测单元的数量，进而增加等离子体回波的有效点数。

图  4  回波信号的多普勒谱图及能量累加图

Fig.  4  Doppler spectrum and energy accumulation diagram

下载: 全尺寸图片 幻灯片

1.4   漂移参数计算

假设电离层测高仪上空的等离子体团作为一个整体进行运动，则每一个散射源的速度矢量均相同^[5]。以电离层测高仪所在位置为坐标原点，以南北方向为$x$轴方向，以东西方向为$y$轴方向，以垂直方向为z轴方向建立坐标系，将等离子体团的运动速度矢量${\boldsymbol{v}}$分解为南北方向矢量${{\boldsymbol{v}}_x}$、东西方向矢量${{\boldsymbol{v}}_y}$、垂直方向矢量${{\boldsymbol{v}}_{\textit{z}}}$，则第i个散射源相对于电离层测高仪所在位置的径向运动速度为${{\boldsymbol{v}}_{\text{R}}}$，可表示为

式中：${\theta _i}$和${\varphi _i}$分别为第i个散射回波的仰角（天顶角的余角）和方位角，其值通过对每个散射源进行波束合成测向得到；c为电波在真空中的传播速度；${f}_{0}$为发射信号载频中心频率；${f_{{\text{d}}i}}$为每个回波信号的多普勒频率；$N$为散射源个数.

根据每个散射源回波的方位角、天顶角、径向速度，采用最小二乘拟合解算等离子体的漂移运动速度矢量，获得南北向、水平向和垂直向速度分量。

2   漂移测量技术验证试验

2.1   试验概述

为了验证本文所提电离层漂移测量技术，于2020年9月在子午工程海南富克站开展了验证试验。其中试验设备为基于该技术自研的电离层测高仪TYC-2；发射天线为正交delta天线，架高32 m、水平跨度60 m；接收天线为四副有源正交环天线，组成边长为60 m的正三角形阵列，与DPS-4D设备的发射天线部署方式一致。两套系统发射天线相距100 m，电离层状态认为是相同的。其他主要工作参数如表1所示.

表  1  试验主要工作参数

Tab.  1  Main working parameters

测高仪	频率步进/ kHz	频率个数	起测时间	积累时间/s
TYC-2	20	20	4分0秒	16.384
DPS-4D	50	8	4分19秒	20.480

下载: 导出CSV 

| 显示表格

从表1可以看出，TYC-2在工作周期的04分0秒开始工作，DPS-4D于04分19秒开始工作，两个系统之间无互相干扰，工作周期为15 min。为了便于整体对比两个系统的性能，约定不同时段的探测频率如下：20点至第二日8点为2 700~3 100 kHz；8点至12点为5 700~6 100 kHz；12点至20点为7 500~7 900 kHz。

2.2   试验结果对比

2.2.1   漂移天空图对比

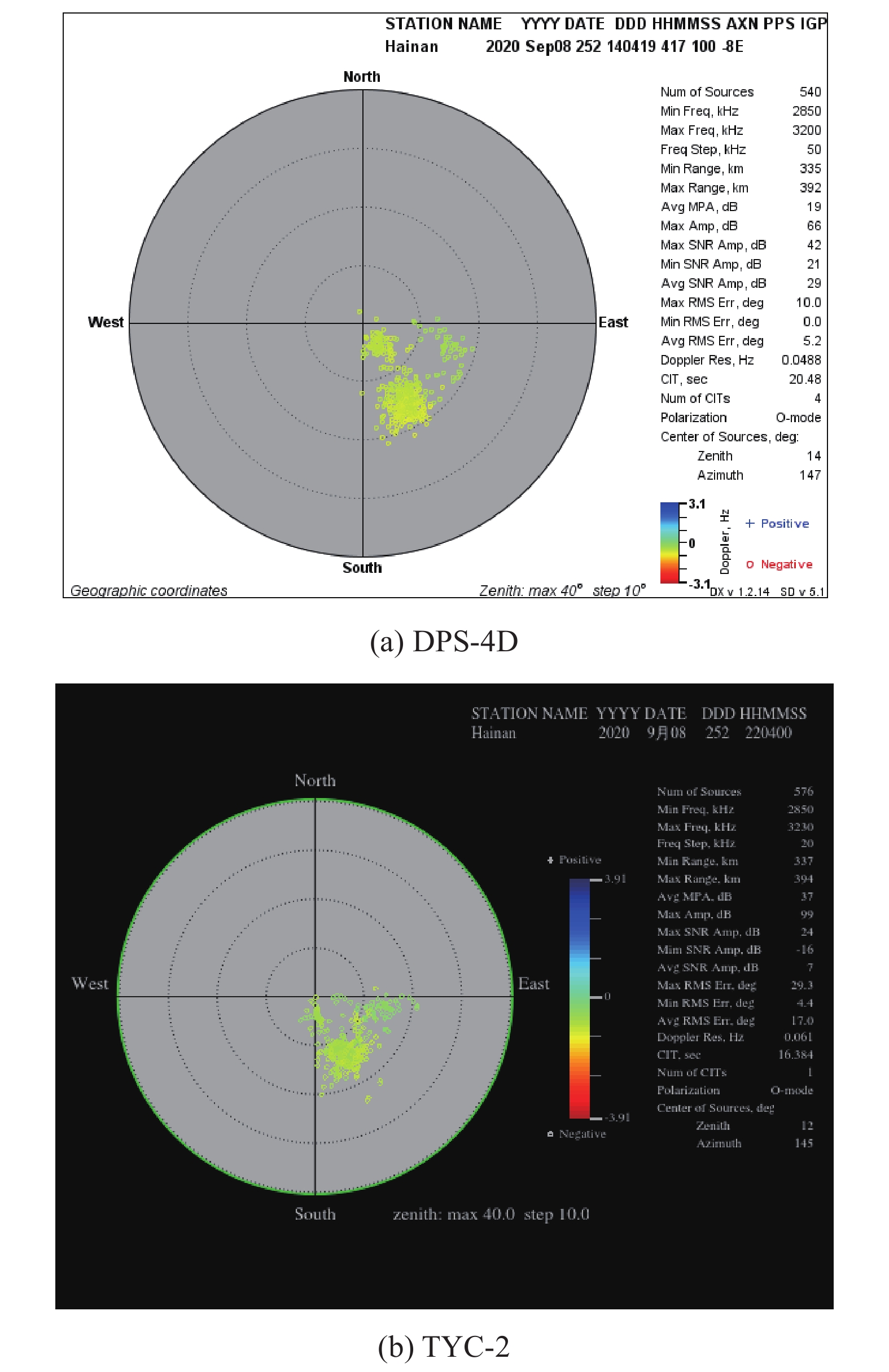
图5给出了两个系统在2020年9月8日典型时刻漂移天空图的结果，其中，图5(a)为DPS-4D测量的天空图（UT），图5 (b)为TYC-2测量的天空图（LT），且两图为同时刻数据。可以看出，等离子体回波信号均来自东南方向，两个系统散射点在空间的分布趋势相一致。

图  5  2020年9月8日两系统的天空图结果对比

Fig.  5  Comparison of sky map results of two systems on Sep. 8, 2020

下载: 全尺寸图片 幻灯片

2.2.2   反射高度对比

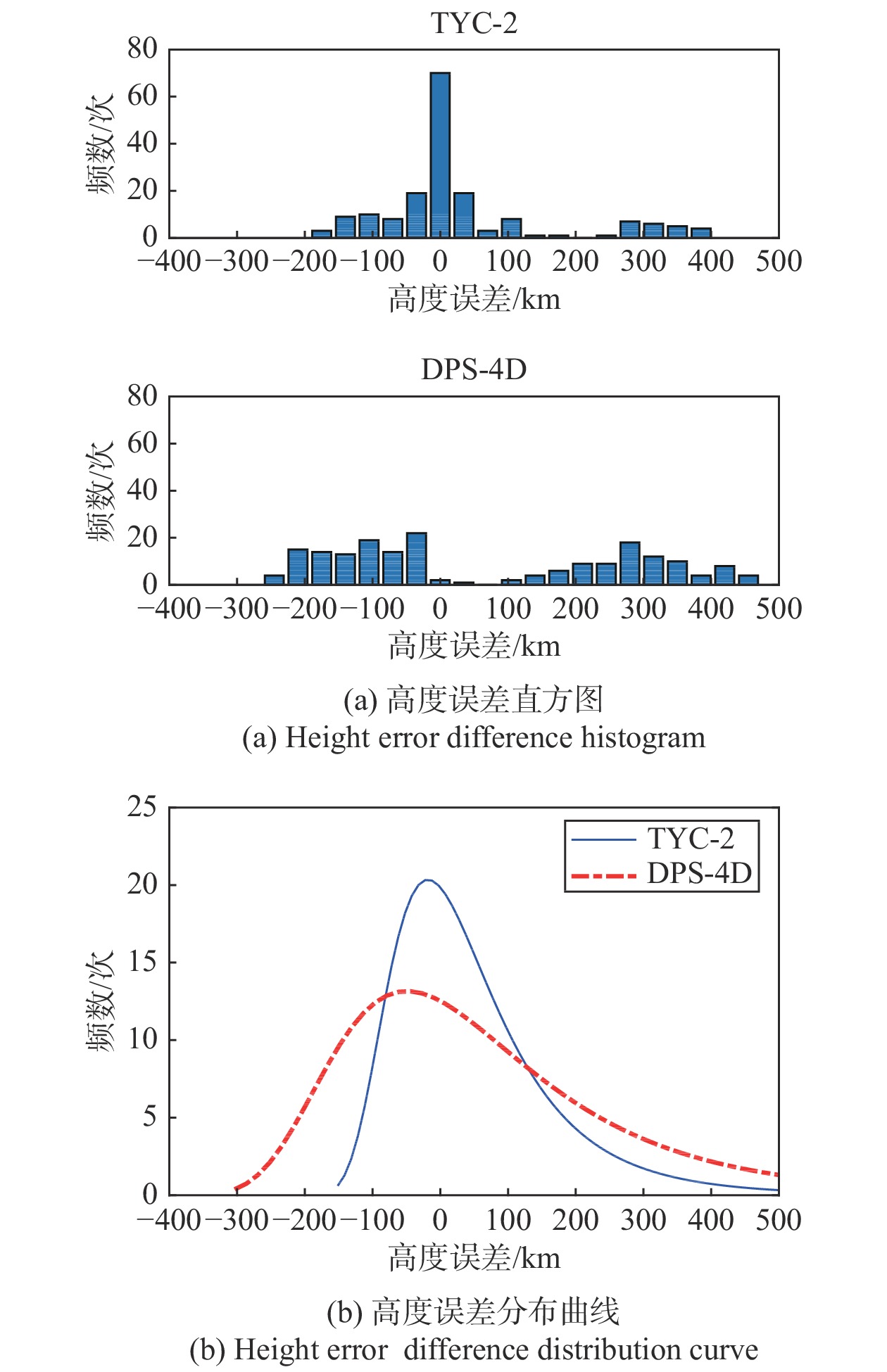
等离子体回波源所在高度确定得越准确，其测量的天空图和漂移速度估计越可靠。为了说明两个系统漂移测量中自动确定的“回波源”所在高度的差异，根据频高图人工确定F模式指定频率的高度范围，并与天空图中回波源的高度范围进行比较，高度差越小，表明高度范围选择得越准确。图6给出了两个系统2020年9月8日的高度误差直方图和分布曲线，可以看出，本文方法的高度误差主要集中在0 km附近，这是因为在确定“回波源”所在高度的算法中，有针对性地去掉了受条状干扰、同频干扰等影响的某些高度单元，进一步确保了用于漂移参数计算所采用的回波源信号是有效的。

图  6  2020年9月8日两系统的等离子体回波源高度误差对比

Fig.  6  Comparison of the height error of plasma return wave source of two systems on Sep. 8, 2020

下载: 全尺寸图片 幻灯片

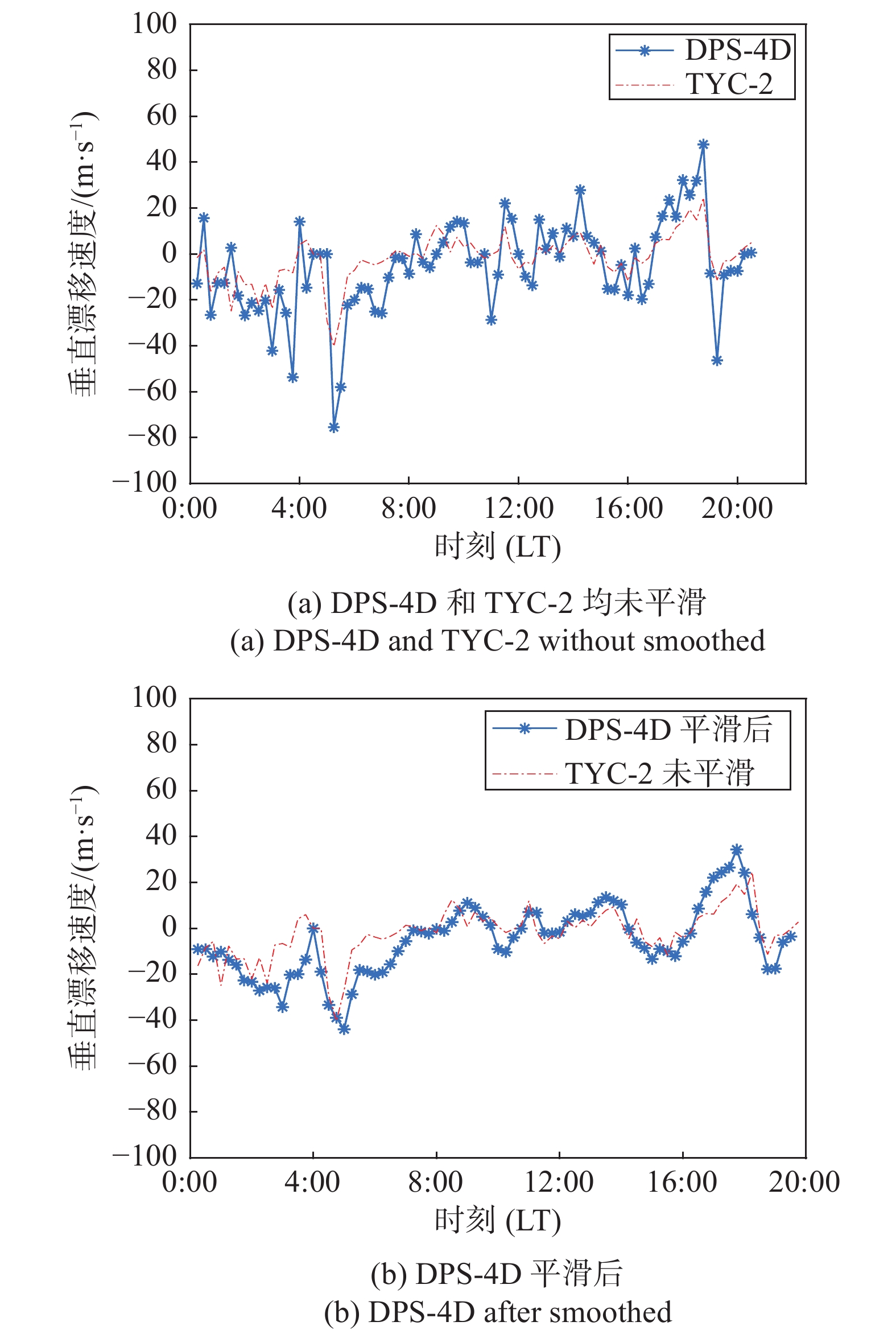
2.2.3   不均匀体漂移速度对比

图7给出了2020年9月8日（LT）同时刻测量的垂直漂移速度对比结果。图7(a)均没有做平滑处理，图7(b)中对DPS-4D数据进行了平滑处理，可以看出，自研电离层测高仪TYC-2测量结果比较平稳，且测量结果符合漂移速度的基本特性^[18]。

图  7  2020年9月8日两系统的等离子体垂直漂移速度对比

Fig.  7  Comparison of ionospheric drift velocity of two systems on Sep. 8, 2020

下载: 全尺寸图片 幻灯片

3   结　论

针对已有等离子体漂移测量技术中干涉仪测向存在相位模糊、短波干扰导致测向误差等问题，改进了基于相控阵垂直探测的电离层漂移测量技术，通过采用波束合成测向技术、干扰避让技术、时间内插技术等方法，提升系统测向的准确性和稳健性。并与海南DPS-4D电离层测高仪对天空图、反射高度、不均匀体漂移速度进行了对比，结果表明，本文所提方法的天空图等离子体空间分布趋势与DPS-4D相一致，反射高度误差更集中，垂直漂移速度更加平稳，进一步表明本文所提方法的有效性。

致谢：感谢试验期间子午工程海南富克站提供的帮助.