引　言

在形成电磁干扰的三要素(电磁骚扰源、耦合途径和敏感设备)中，电磁骚扰源是产生电磁干扰的源头，对其开展监测、定位与研究有助于科学分析电磁干扰的成因，可为解决电磁兼容与电磁防护问题提供技术支撑^[1]。局部放电源是一种常见的电磁骚扰源，高压变电站和输电线路中的高压局部放电、发动机的电点火系统、人体静电放电以及电气开关动作等均会产生瞬态电磁辐射^[2-4]，且其电磁辐射信号在时域上具有典型的脉冲特性，在频域上占有较宽的频谱范围，所引发的电磁干扰问题尤为突出。此外，利用局部放电源所蕴含的特征信息，还可以实现对电气设备故障的早期预警与识别定位等。因此，国内外学者围绕局部放电源的探测定位均开展了大量研究工作。比如，美国贝尔实验室的Don L. Lin等人^[5]基于到达时间差(time difference of arrival，TDOA) 定位原理，利用四元接收天线阵列在生产厂房内实现了对静电放电源的准确定位；英国Bath大学的P. J. Moore等人^[6-7]相继开发了便携式、车载移动式等变电站局部放电监测系统，可在一定区域范围内实现对局部放电源的准确定位。国内的重庆大学、上海交通大学、华北电力大学等单位在该领域也开展了相关研究^[8-10]，并取得了丰硕成果。

上述基于接收天线阵列等开展的局部放电源探测定位研究，计算得到的通常是局部放电源的空间三维坐标值，现场测试人员难以直接、快速将其与产生局部放电电磁辐射的实体物理模型相关联，还需要借助其他测试手段在实际应用场景中进行测量，以实现对局部放电源所对应实际发生位置的匹配，整个过程耗时费力且容易引入其他测量误差，不利于实现电磁干扰源的快速排查与定位。

针对上述问题，本文结合实际工程应用需求，通过引入计算机视觉^[11]，研究提出了一种基于P3P (pespective-3-point)相机位姿估计^[12-14]的局部放电源可视化标注方法。该方法在获取局部放电源空间三维坐标的基础上，通过融合视觉场景信息，可以实现对其所对应实体物理模型的可视化标注，有利于直观、快速开展局部放电源的排查与定位，为科学分析电磁干扰成因等提供参考依据。

1   局部放电源可视化标注原理

1.1   相机投影模型

为实现局部放电源的可视化标注，需要构建真实世界中三维空间点到二维图像中像素点的相机投影模型，以确定三维空间中电磁辐射源在二维图像上的准确位置。

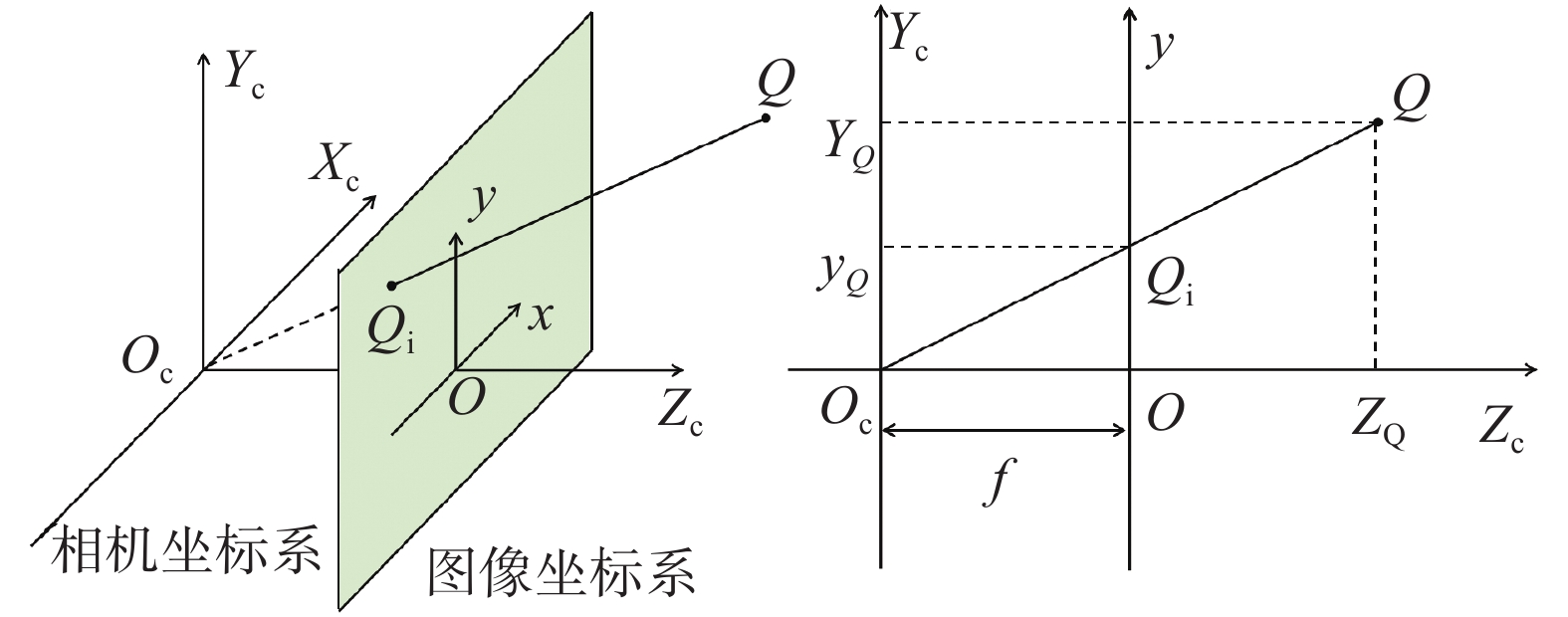
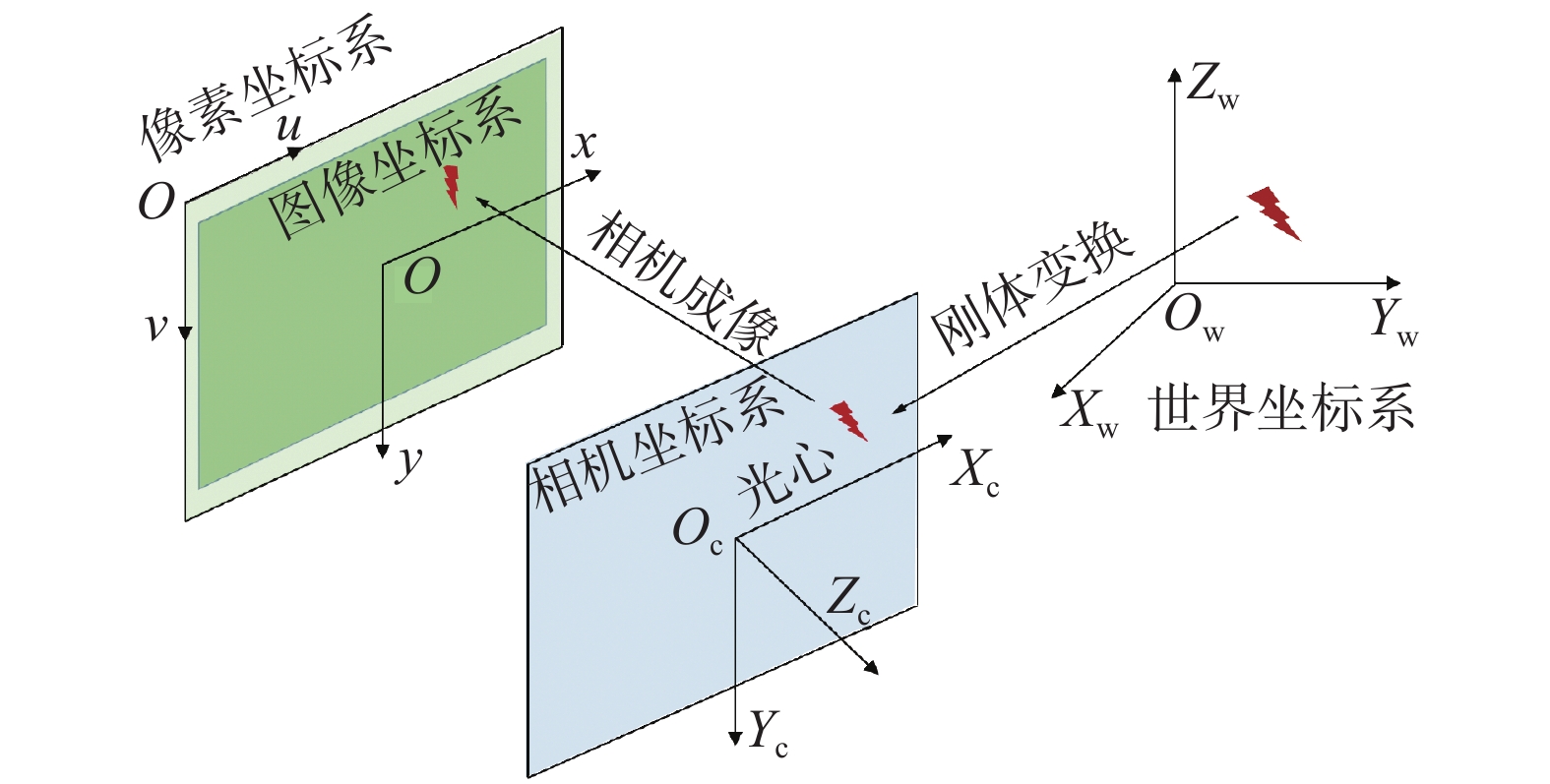
相机投影模型主要由刚体变换模型和相机成像模型两部分构成，并涉及到世界坐标系、相机坐标系、图像坐标系和像素坐标系等4个坐标系之间的相互转换^[15]。上述4个坐标系之间的关系示意图如图1所示。图1中，O_wX_wY_wZ_w为世界坐标系；O_cX_cY_cZ_c为相机坐标系，原点位于相机镜头的光心；xOy为图像坐标系；uOv为像素坐标系。其中，世界坐标系中的点可通过刚体变换模型转换到相机坐标系，刚体变换参数在相机投影模型中称为相机的外部参数，也称为相机位姿参数，以下统称后者；相机坐标系中的点可通过相机成像模型投影到像平面坐标系，本文采用的是线性成像模型，即基于小孔成像原理的针孔相机成像模型，其原理图如图2所示。

图  1  相机投影模型空间坐标系示意图

Fig.  1  Schematic of the spatial coordinate system of the camera projection mode

下载: 全尺寸图片 幻灯片

图  2  针孔相机成像原理图

Fig.  2  Schematic of the pinhole camera imaging

下载: 全尺寸图片 幻灯片

图2中点Q位于相机坐标系中，点Q_i为其在图像坐标系的投影点，f为相机焦距。利用相机焦距构建相似三角形，可以根据Q点的坐标求解出Q_i点在图像坐标系中的坐标，实现三维空间点到二维空间点的转换。在此基础上，通过平移转换以及长度单位与像素单位的转换，可以将图像坐标系中的点转换到像素坐标系中。其中，相机焦距、平移转换参数和单位转换参数等称为相机内参，相机内参可以通过相机标定获取^[16]。

综上，构建完成的相机投影模型见式(1)：

式中：s为深度因子；[u, v, 1]为局部放电源在二维图像中的齐次像素坐标；K为相机内参矩阵；R为相机位姿参数矩阵中的旋转矩阵；t为相机位姿参数矩阵中的平移矩阵；R，t也被合称为相机位姿参数；[X_w,Y_w,Z_w,1]为局部放电源在世界坐标系中的齐次坐标；P为相机的投影矩阵。

1.2   相机位姿参数求解方法

根据式(1)，为实现对三维空间中局部放电源的可视化标注，需要获取局部放电源的三维空间坐标和相机的内参矩阵K、相机位姿参数R，t。其中，局部放电源的三维空间坐标可以通过构建多元接收天线阵列和基于TDOA的目标定位方法计算得到^[17]，相机内参矩阵K可以通过相机标定计算得到^[18]，本文不再赘述。下面主要介绍基于P3P的相机位姿参数R和t的求解方法。

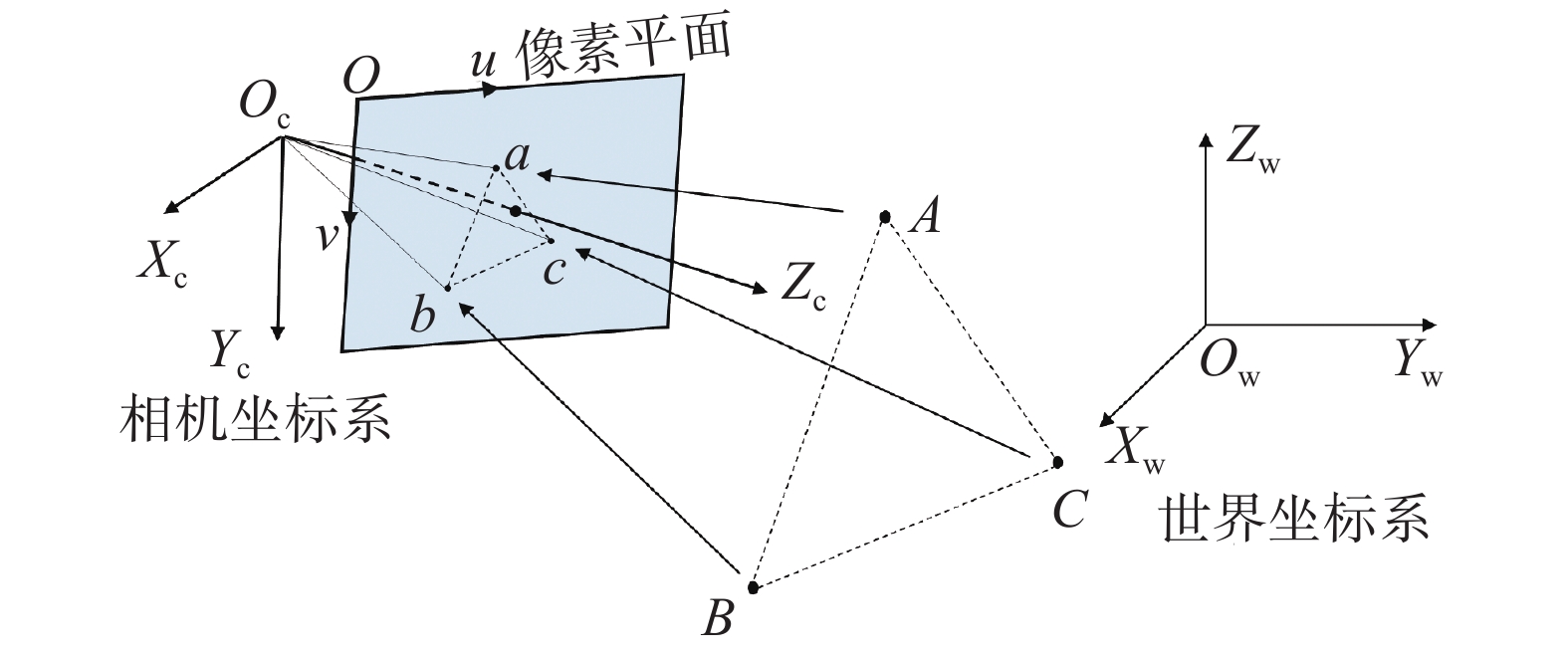
基于P3P技术求解相机位姿参数的基本原理如图3所示。

图  3  相机位姿参数求解示意图

Fig.  3  Schematic of solving camera pose parameters

下载: 全尺寸图片 幻灯片

图3中，假设在世界坐标系中存在3个不共线的控制点A, B, C，其在像素平面坐标系中的投影点分别记为a，b，c，由此可以构成3组3D-2D点对。根据余弦定理，这3组点对在相机坐标系中的关系见式(2)：

记：

将式(2)两边同除以||O_cC||²，有

根据式(3)，通过代入至少3组3D-2D点对坐标，即可求解得到式中的未知参数x，y。该方程最多能得到4个解，但可以用验证点来计算最可能的解，所以在实际应用中通常选取4组点对来确定唯一解。求解得到x和y值后，根据式(4)可计算出A点在相机坐标系中的三维坐标。

通过式(4)可以确定$\left\| {O_{\rm{c}}C} \right\|$，最后利用向量公式$OC = O_{\rm{c}}c \cdot \left\| {O_{\rm{c}}C} \right\|$，可以求得C点在相机坐标系下的坐标。同理可求得A点和B点在相机坐标系下的坐标。

由A，B，C在世界坐标系中的三维坐标已知，根据这3点在相机坐标系和世界坐标系中的关系，可以根据式(5)构建最小二乘问题来求解得到相机位姿参数R和t。

式中：h_i为选择的控制点在相机坐标下的坐标；${{\boldsymbol{h}}_i^\prime }$为选择的控制点在世界坐标系下的坐标；i的取值为从1到3，对应A，B，C三个世界坐标点。在此基础上，通过额外添加具有真实世界坐标的验证点，可以验证本算法所获取相机位姿参数的准确性。

综上所述，在三维空间中选择至少3个不共线的控制点，再添加一个验证点，基于P3P技术就可以求解得到相机位姿参数R和t。

为实现对控制点坐标的快速、准确计算，本文采用可被计算机自动识别的ArUco标识^[19]，如图4所示，并利用ArUco标识的角点作为控制点。相机通过拍摄含有ArUco标识的场景图像，可由计算机自动识别出ArUco标识角点在图像中的像素坐标。结合ArUco标识角点在世界坐标系中的三维坐标，利用式(5)可求解出相机的R，t参数值，从而得到相机投影模型中的相机位姿参数。为提高R和t的求解精度，本文使用4个不共线的控制点，并在相机位姿参数求解之前对图像进行畸变矫正^[20]。

图  4  典型的ArUco标识

Fig.  4  Typical ArUco logo

下载: 全尺寸图片 幻灯片

1.3   局部放电源可视化标注步骤

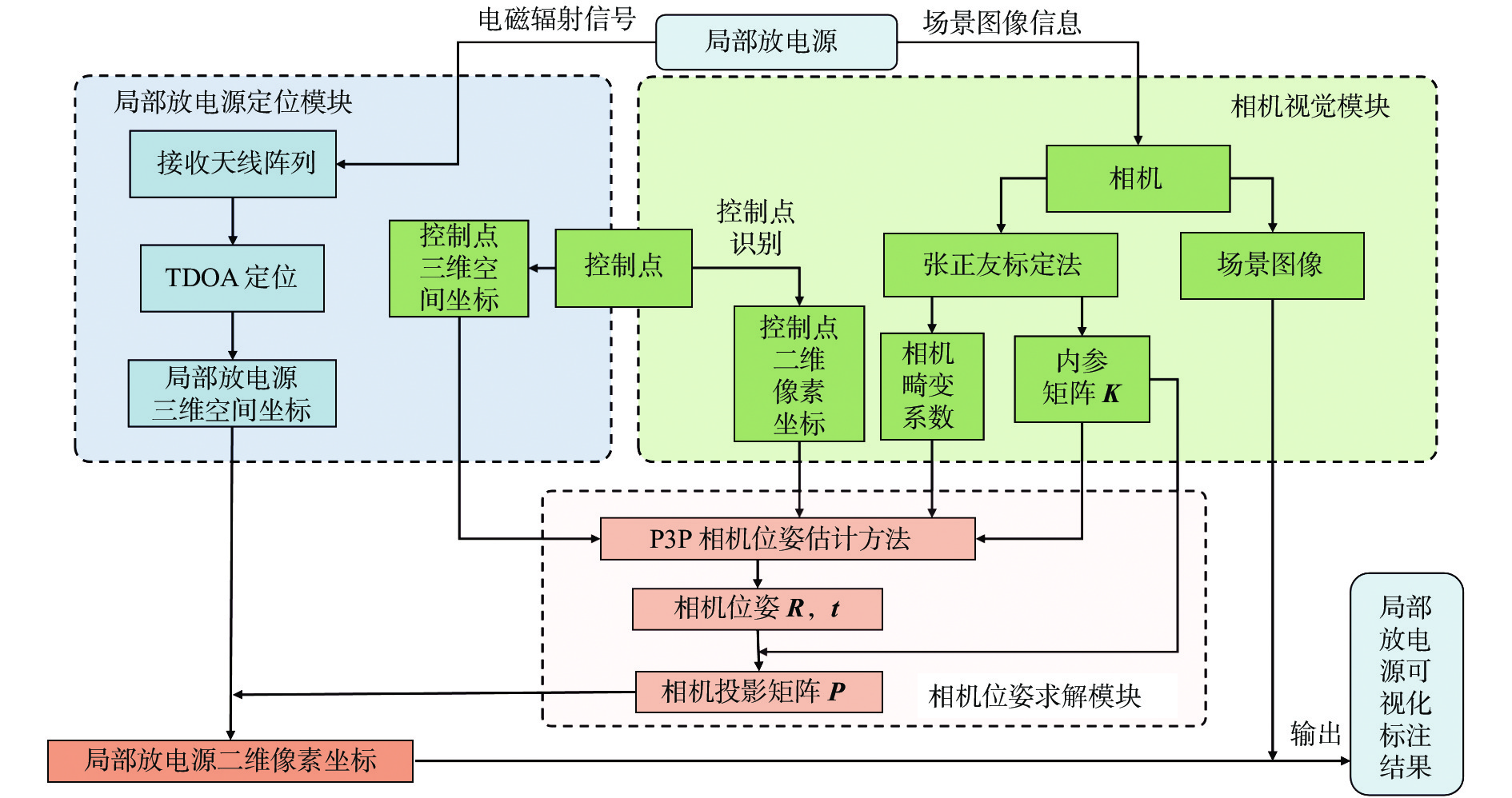
本文提出的局部放电源可视化标注方法主要由局部放电源定位模块、相机视觉模块和相机位姿求解模块3部分组成，如图5所示。局部放电源的可视化标注步骤如下：

图  5  局部放电源可视化标注原理框图

Fig.  5  Block diagram of visual labeling of partial discharge radiation source

下载: 全尺寸图片 幻灯片

1）在待检测区域内，布设用于响应局部放电电磁辐射信号的多元接收天线阵列，并基于TDOA等定位算法求解出局部放电源在天线阵列所组成世界坐标系中的三维坐标；

2）对拍摄场景信息的相机进行标定，获取相机的内参矩阵K和畸变系数；

3）在世界坐标系中放置ArUco标识，记录其中4个不共线角点(控制点)的三维空间坐标，并使用相机拍摄包含控制点的场景图像，自动计算控制点在图像中的二维像素坐标；

4）根据式(5)求解相机位姿参数R，t；

5）利用K，R，t等参数构建相机投影矩阵P，并根据式(1)和局部放电源的三维坐标，计算出局部放电源对应的像素坐标完成目标标注。

2   可视化标注模拟测试与误差分析

根据前面描述的局部放电源可视化标注方法基本原理及其实施步骤可见，影响局部放电源可视化标注准确性的因素主要来自两个方面：一是局部放电源定位的准确性，即其空间三维坐标求解的准确性；二是相机投影模型的准确性，即相机内参、位姿参数等参数求解的准确性。因此，本节将通过构建模拟测试场景，分析局部放电源空间定位误差，以及相机内参、位姿参数等参数求解误差对局部放电源可视化标注准确性的影响。

2.1   模拟测试场景设置

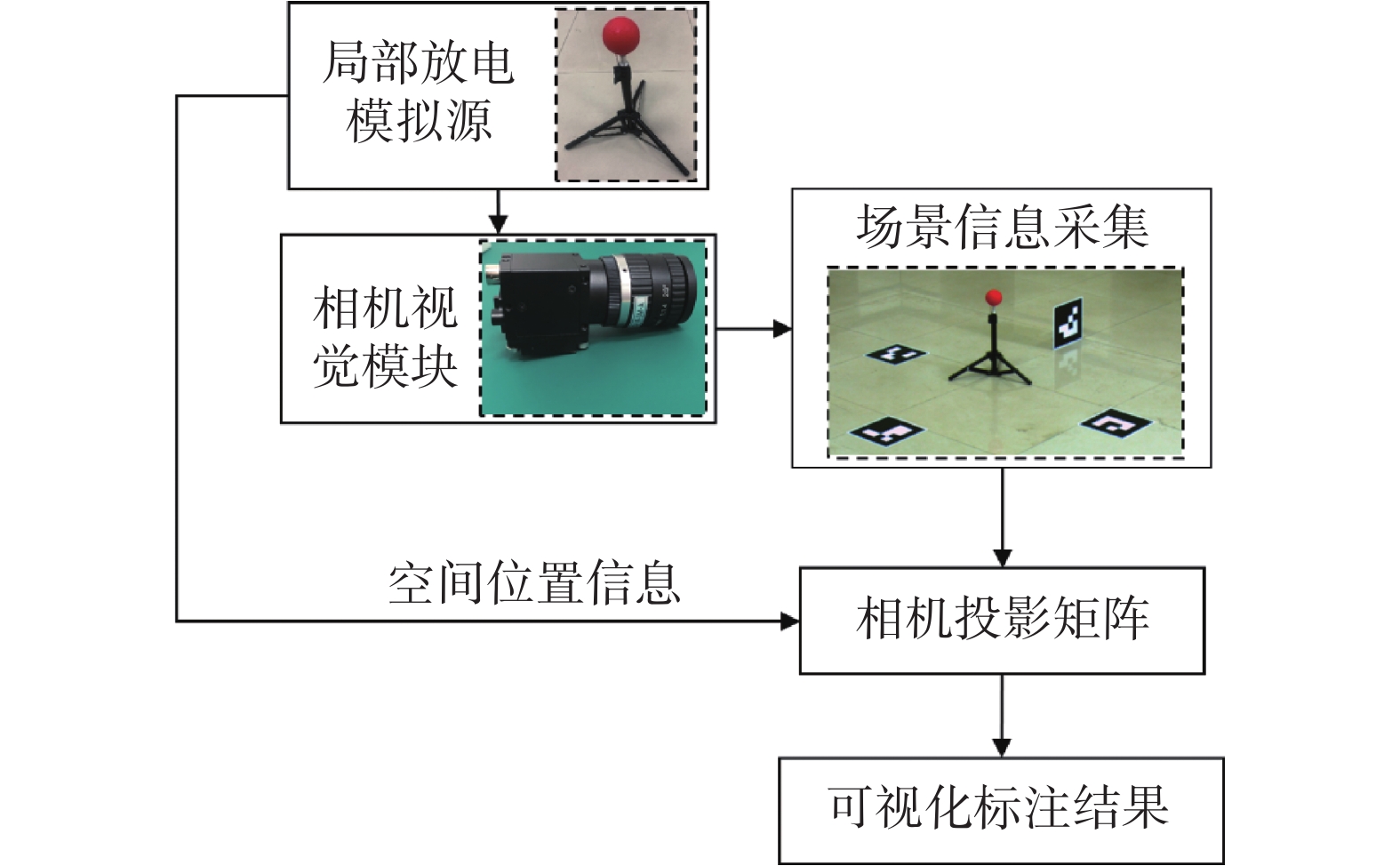
搭建的模拟测试场景框图如图6所示。为便于对标注结果开展定量分析，在图6中利用1个直径为7 cm的红色圆球模拟表征待标注的局部放电源(以下简称模拟源)，其中心点的三维坐标表示该模拟源的中心位置。进行场景拍摄的工业相机具有500万有效像素，镜头采用焦距为6 mm的定焦镜头。

图  6  模拟测试场景框图

Fig.  6  Block diagram of simulation test scenario

下载: 全尺寸图片 幻灯片

根据1.3节中给出的可视化标注步骤，模拟源的三维坐标从图6中红色圆球的中心点处获取。对图6中所使用的相机进行标定，计算得到的相机内参矩阵K和畸变系数见表1，此时相机的重投影误差为0.34 px。

表  1  相机内参矩阵K及畸变系数

Tab.  1  Camera internal parameter matrix K and distortion coefficient

内参矩阵K	$\left[ {\begin{array}{*{20}{c}} {2.55 \times {{10}^3}}&0&{{\text{1}}{\text{.01}} \times {{10}^3}} \\ {0{\text{ }}}&{{\text{2}}{\text{.55}} \times {{10}^3}}&{8.03 \times {{10}^2}} \\ 0&0&1 \end{array}} \right]$
畸变系数	(−0.14，0.86，0.00，0.00，−2.60)

下载: 导出CSV 

| 显示表格

在世界坐标系中放置ArUco标识，记录其中4个不共线角点(控制点)的三维空间坐标，并计算得到控制点在图像中的二维像素坐标，见表2。

表  2  ArUco标识控制点坐标

Tab.  2  ArUco identification control point coordinates

控制点序号	空间坐标/m	角点像素坐标/px
1	(0，0.60，0.20)	(1162.45，985.08)
2	(0.60，0，0.00)	(1233.03，1166.14)
3	(0，−0.60，0)	(696.81，1185.43)
4	(−0.60，0，0.00)	(716.54，1002.72)

下载: 导出CSV 

| 显示表格

根据表1、表2数据和式(5)，求解得到相机位姿参数R，t，见式(6)：

利用K，R，t等参数构建相机投影矩阵，输入模拟源空间坐标，实现对其可视化标注，结果如图7所示。其中，标注框采用圆形标注框，标注框直径为7 cm。本文引入交叠率^[21]，即标注框和目标交集(相交面积)与并集(总面积)的比值，作为评价标注结果是否准确地量化指标。交叠率越接近于1，标注的准确性越高；通常认为交叠率≥0.5就是较好的标注结果。根据图7所示的标注结果，计算得到的交叠率为0.94.

图  7  模拟源可视化标注结果

Fig.  7  Visualized labeling result of simulated source

下载: 全尺寸图片 幻灯片

在完成上述相机位姿估计的基础上，改变模拟源所处位置，利用其三维坐标和相机投影矩阵计算得到的可视化标注结果如图8所示。根据图8计算得到的交叠率为0.96，说明本文提出的可视化标注方法是准确可行的。

图  8  模拟源位置改变后的可视化标注结果

Fig.  8  Visualized labeling result of the simulated source after position has changed

下载: 全尺寸图片 幻灯片

2.2   影响标注准确性的因素分析

根据本文提出的可视化标注原理，影响局部放电源可视化标注准确性的影响因素主要来自以下3个方面：局部放电源空间坐标的定位误差、相机位姿参数误差、相机内参重投影误差。

2.2.1   局部放电源空间坐标定位误差的影响

这里依然利用直径为7 cm的红色圆球模拟表征待标注的局部放电源(以下简称模拟源)，并选取一个交叠率达到0.99的标注结果所对应的圆形标注框作为参考基准。

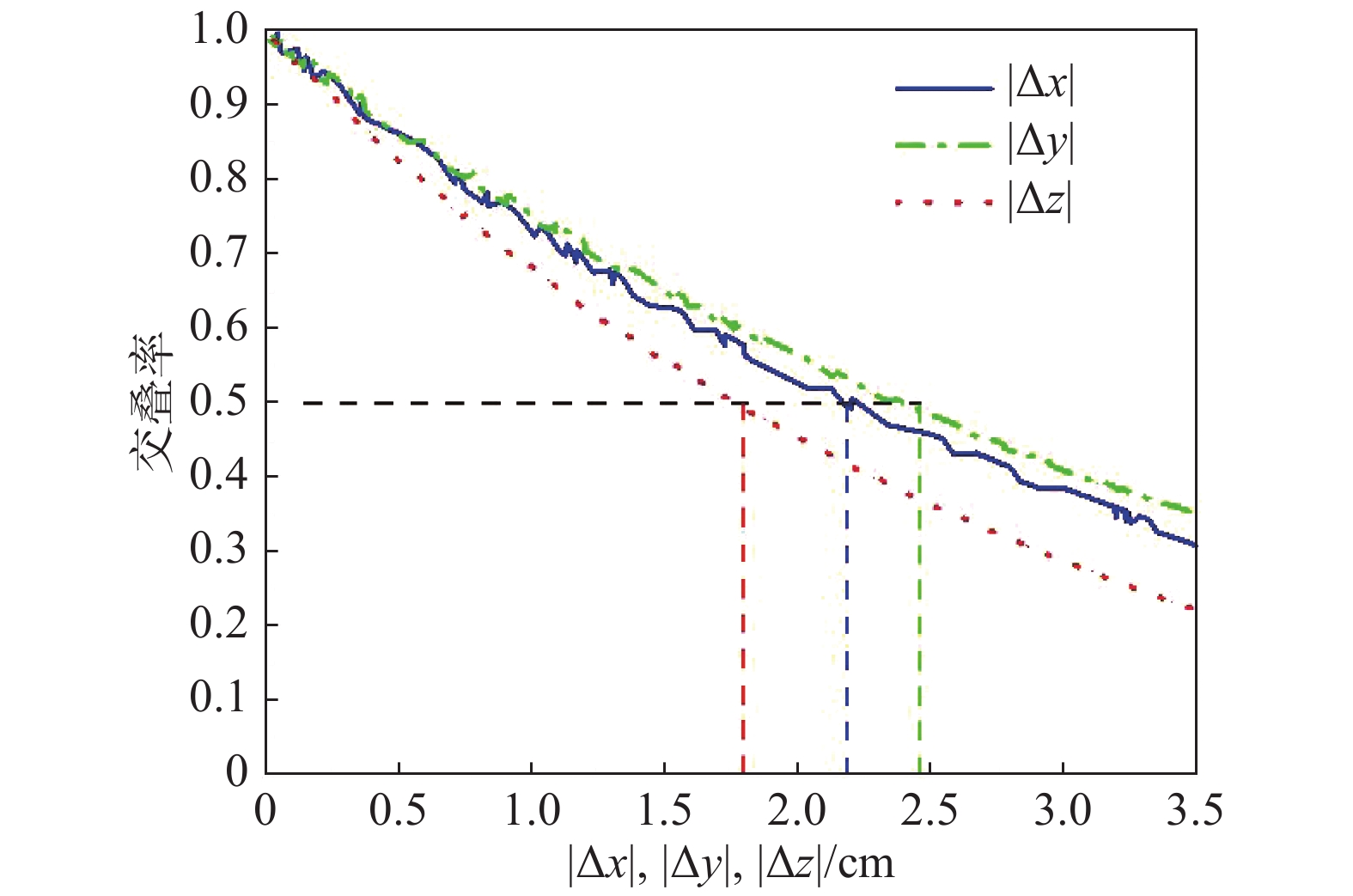
为评估模拟源空间坐标定位误差对标注结果的影响，分别在模拟源空间坐标的3个方向上(x方向、y方向和z方向)添加误差$\Delta x$，$\Delta y$和$\Delta {\textit{z}}$，误差绝对值的最大值设置为1/2圆球直径，即在[0, 3.5] cm范围内随机取值，通过100次模拟，计算每次定位结果所对应标注结果的交叠率，结果如图9所示。

图  9  |∆$x$|，|∆$y$|和|∆${\textit{z}}$|对标注交叠率的影响

Fig.  9  Influence of |∆x|, |∆y| and |∆z| on labeling overlap rate

下载: 全尺寸图片 幻灯片

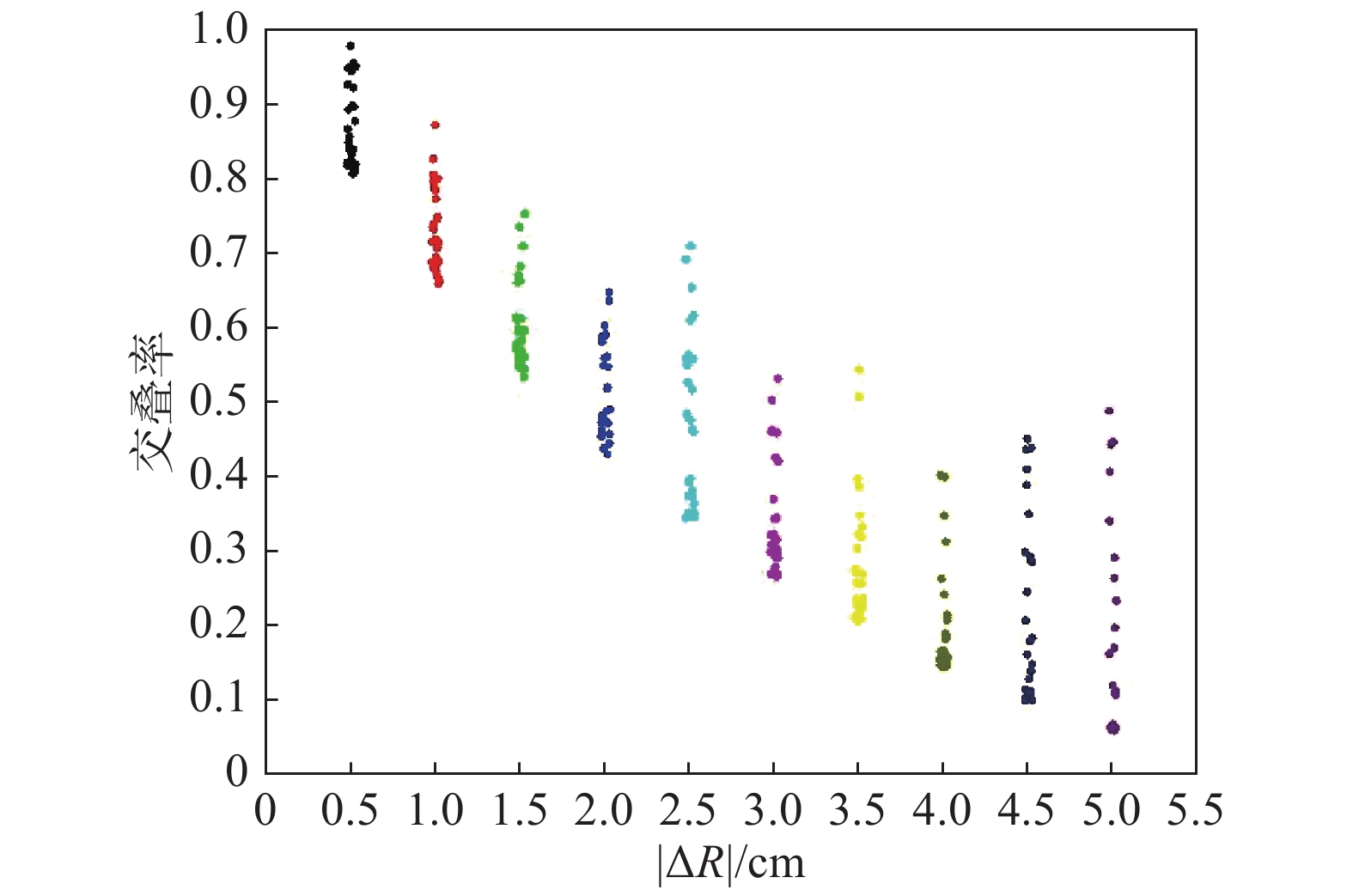
从图9可以看出，在不同方向上，随着模拟源定位误差的增大，标注结果对应的交叠率均随之降低。在x，y，z方向上，当定位误差绝对值分别达到2.20 cm，2.34 cm，1.75 cm时，交叠率下降至0.5，但在不同方向上交叠率随定位误差增大而下降的速率不同，这与相机的视角有关。在此基础上，在3个方向上随机给模拟源的定位坐标添加误差，使其产生定位距离误差$\Delta R$，且$\Delta R = \sqrt {{{(\Delta x{\text{)}}}^{\text{2}}} + {{(\Delta y{\text{)}}}^{\text{2}}} + {{(\Delta {\textit{z}}{\text{)}}}^{\text{2}}}}$，得到$\Delta R$对标注交叠率的影响如图10所示，其中，每个$\Delta R$对应取值随机模拟30次。

图  10  |∆R|对标注交叠率的影响

Fig.  10  Effect of |∆R| on labeling overlap rate

下载: 全尺寸图片 幻灯片

从图10可以看到，随着$\Delta R$的增加，交叠率有整体下降的趋势。但对应于每个$\Delta R$值，30次随机模拟得到的交叠率有高有低，即在$\Delta R$增大的情况下，交叠率并不是单调降低，也有可能不变甚至增加。这主要是因为受相机视角影响，在x，y，z不同方向上随机选取误差偏移量的时候，会有部分误差的空间偏移方向出现在相机光心与模拟源之间的连线上或其周围区域，导致空间位置上虽然存在偏差，但从三维空间转换成二维图像时的偏差反而不明显，从而使得交叠率并不单调降低。

2.2.2   相机位姿参数R，t误差的影响

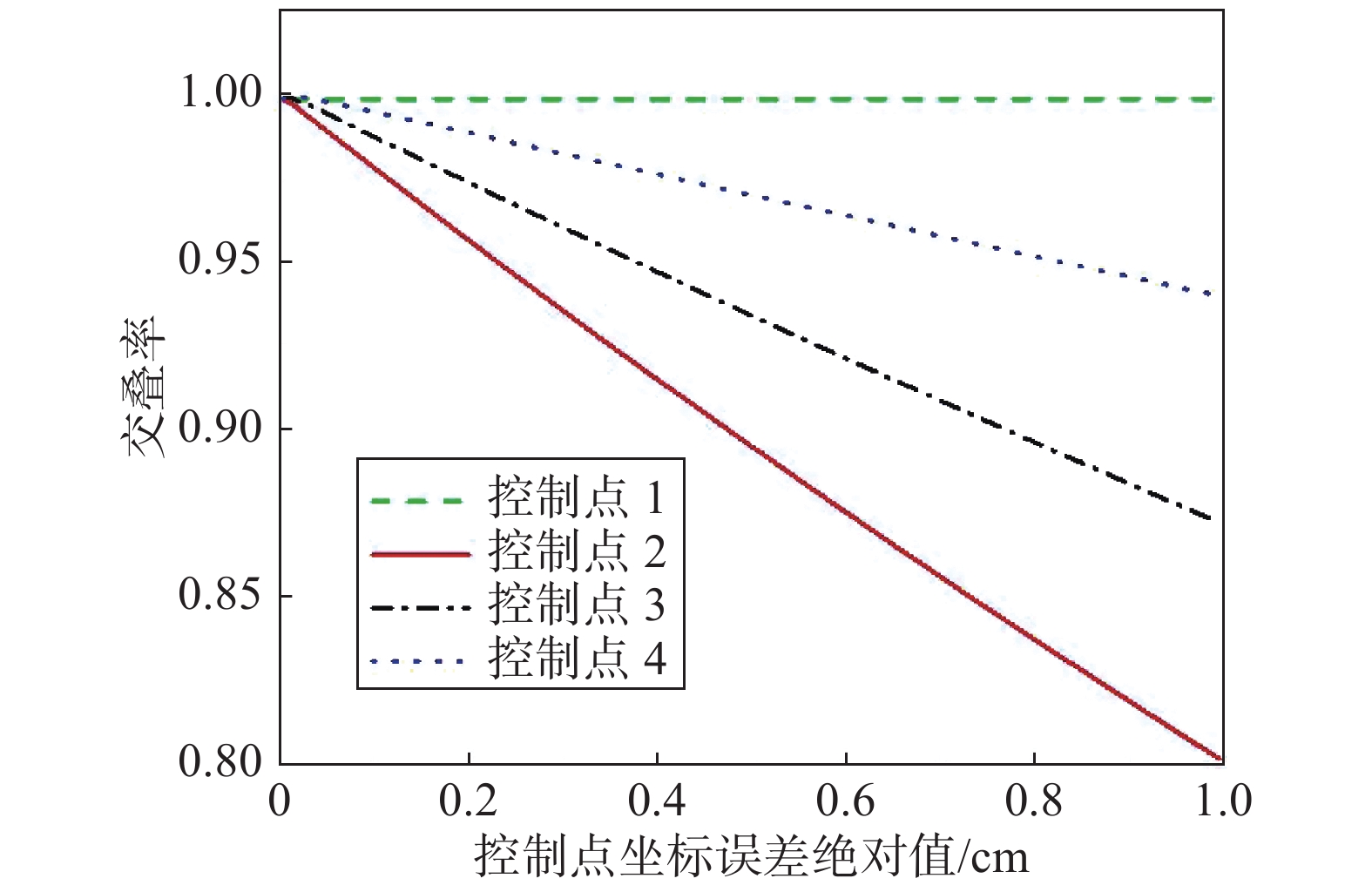
根据控制点坐标和式(5)，可以计算得到相机位姿参数R，t。因此，相机位姿参数R，t对标注结果的影响主要来自控制点坐标误差的影响。在相机内参矩阵不变的情况下，分别对4个控制点添加范围在[0, 1] cm的随机距离误差，进行4组模拟测试，每组通过100次模拟，得到的交叠率如图11所示。

图  11  控制点坐标误差对标注交叠率的影响

Fig.  11  Influence of control point coordinate error on labeling overlap rate

下载: 全尺寸图片 幻灯片

从图11可以看出，随着控制点坐标误差的增大，标注交叠率有所降低，但总体都在0.8以上。其中，控制点1距离相机最远，其坐标误差对标注交叠率的影响最小；控制点4距离相机最近，其坐标误差对标注交叠率的影响最大。由此可见，所选择的控制点距离相机的位置越近，其坐标误差对模拟源标注准确性的影响越大。在实际应用中，控制点的选择可以人工操作，其坐标误差可以控制在较小的范围内，由此计算得到的相机位姿参数R，t对标注结果的影响相对较小。此外，为进一步提升电磁辐射源的标注精度，也可以使用双目相机进行标定，此时控制点误差(相机位姿参数R，t)对标注结果的影响基本可以忽略^[22]。

2.2.3   相机内参重投影误差的影响

相机内参的重投影误差是在相机标定过程中计算得到的。在相机摆放位置不变的情况下，通过多次相机标定可以得到具有不同重投影误差的相机内参矩阵，并计算得到对应的标注交叠率，结果见表3。从表3可以看出，随着重投影误差的增大，标注交叠率有降低的趋势，但总体均大于0.8，可以满足局部放电源的标注需要。根据相机标定要求，重投影误差通常应控制在≤0.50 px，而满足该条件的标注交叠率≥0.9。因此，相机内参的重投影误差对局部放电源标注准确性的影响较小。

表  3  重投影误差对交叠率的影响

Tab.  3  Effect of reprojection error on overlap rate

重投影误差/px	交叠率
0.34	0.99
0.47	0.91
0.54	0.89
0.58	0.82

下载: 导出CSV 

| 显示表格

2.3   模拟测试结果分析

通过开展局部放电源可视化标注模拟测试，并对影响标注结果准确性的因素进行对比分析，可以看出：1)给定模拟局部放电源三维坐标的基础上，计算得到的标注交叠率为0.94，验证了可视化标注方法的准确性；2)局部放电源空间定位坐标误差的增大会导致标注交叠率降低至0.5以下，这也是影响整个可视化标注系统标注结果准确性的主要因素；3)相机内参、外参等相机投影模型参数误差对标注结果也有影响，但总体标注交叠率均在0.5以上，对标注结果准确性的影响相对较小。

3   局部放电源可视化标注试验验证

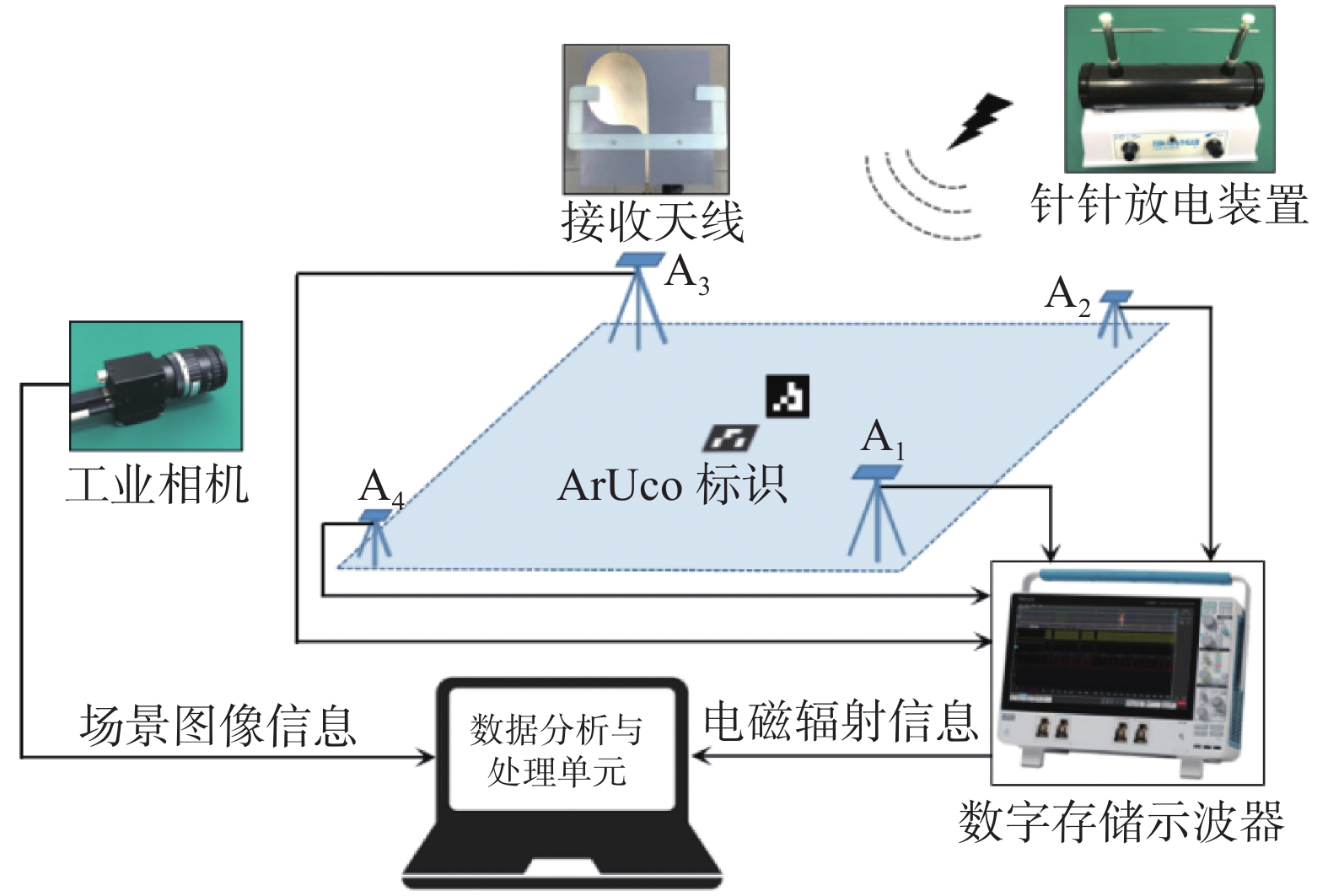
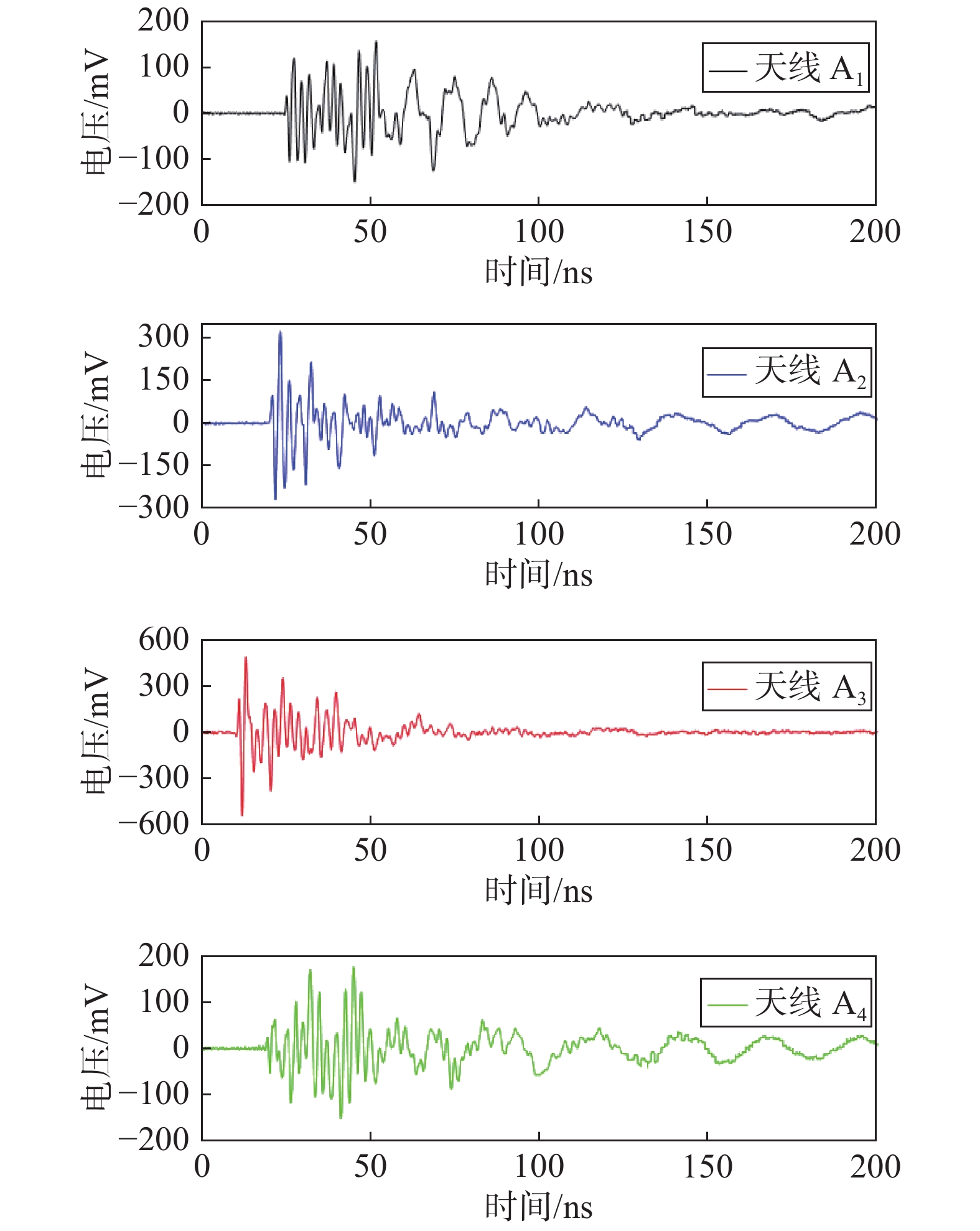
试验整体配置框图如图12所示，其主要由直流高压发生器、四阵元接收天线、工业相机、高速数字存储示波器、数据分析与处理单元等构成。其中，利用直流高压发生器构建针针放电装置，模拟产生一个局部放电源；接收天线采用自研的Vivaldi天线（输出端接20 MHz~1 GHz带通滤波器以提高接收信号信噪比），组成一个高低四元接收天线阵列，接收天线之间的间距设置为3 m，A₁，A₃天线的离地高度为1.34 m，A₂，A₄天线的离地高度为0.63 m，配合四通道高速数字存储示波器（模拟带宽4 GHz，最高采样率20 GS/s），完成局部放电电磁辐射信号的接收、数据采集与存储；工业相机负责完成试验场景的实时监测与图像采集，其靶面尺寸为宽8.8 mm、高6.6 mm、对角线11 mm，具有500万有效像素和定焦8 mm镜头，该相机放置在距离针针放电装置6.23 m的位置，离地高度为1.50 m；数据分析与处理单元主要利用课题组开发的数据处理算法和计算机上位机，开展相机标定，建立相机投影模型，并基于TDOA定位原理和布谷鸟优化搜索算法，计算得到局部放电源的空间坐标，实现对局部放电源的可视化标注。

图  12  试验验证场景框图

Fig.  12  Block diagram of experiment scenario

下载: 全尺寸图片 幻灯片

根据1.3节的可视化标注步骤，在待检测区域内布设一个高低四元阵，并利用高速数字存储示波器获取高压放电电磁辐射信号的时域波形(采样频率设置为10 GHz)，结果如图13所示。基于TDOA定位原理和布谷鸟优化算法，计算得到高压放电源在世界坐标系中的三维坐标为(5.73, −5.14, −0.41) m。

图  13  实测高压放电电磁辐射信号

Fig.  13  Measured electromagnetic radiation signal of high voltage discharge

下载: 全尺寸图片 幻灯片

开展相机标定，并利用试验场景中放置的ArUco标识，选取4个不共线控制点，分别计算得到K，R，t等参数（结果见式(7)和式(8)），完成相机投影模型的构建。

结合本次试验所用针针放电装置的整体尺寸，将标注框设置为半径等于10 cm的圆形框，基本可以涵盖放电装置所在的区域。根据高压放电源的三维坐标和相机投影模型，计算得到该放电源在场景图像中的像素坐标为(1169.79，595.34) px，利用圆形标注框对其进行可视化标注，结果如图14所示(图中红色圆圈为实测的标注框)。从图14可以看出，标注框所在的区域基本覆盖了针针放电所产生的区域，对高压放电电磁辐射源的指向性好，实现了对放电源的可视化标注。以图14中针针放电的中心位置为圆心，绘制半径为10 cm的圆形框作为标注结果对照的基准框，计算得到标注框与基准框的交叠率为0.67.

图  14  高压放电源标注结果I（蓝色圆圈为基准框，红色圆圈为标注框）

Fig.  14  Labling result I of high voltage discharge source (the blue circle is the reference frame, and the red circle is the labeling frame)

下载: 全尺寸图片 幻灯片

为进一步验证标注方法的可行性和准确性，通过改变高压放电源位置等参数，对放电源再次进行可视化标注试验，结果如图15所示。根据图15计算得到标注框与基准框的交叠率为0.72。

图  15  高压放电源标注结果II（蓝色圆圈为基准框，红色圆圈为标注框）

Fig.  15  Labling result II of high voltage discharge source (the blue circle is the reference frame, and the red circle is the labeling frame)

下载: 全尺寸图片 幻灯片

上述试验测试结果表明，本文方法通过融合场景图像信息与电磁辐射信息，在对局部放电源实现空间定位的基础上，可以对其进行可视化标注，使局部放电源定位结果显现更加直观，有利于对其开展快速排查与定位。

4   结　论

本文通过协同监测场景图像信息与电磁辐射信息，研究提出了一种基于相机位姿估计的局部放电源可视化标注方法，给出了该方法的实施流程，并对其可行性与准确性进行了模拟测试和试验验证，研究结果表明：

1）通过求解相机内参矩阵与位姿参数，构建相机投影模型，可以将局部放电源的三维空间定位结果转换为场景图像中的像素坐标，从而实现对局部放电源的可视化标注。该方法中接收天线和相机所处位置相对独立，可根据实际需求灵活放置，有利于进一步拓展其应用场景。

2）局部放电源空间定位误差、相机投影模型参数误差等均会直接影响局部放电源可视化标注结果的准确性。通过模拟测试并引入交叠率计算可以看出：利用交叠率可以定量评价标注结果的准确性；相机内参、外参等相机投影模型参数误差对标注结果的影响较小；局部放电空间定位误差是影响标注结果准确性的主要因素。

3）利用直流高压发生器和针针放电装置模拟产生局部放电源，基于高低四元接收天线阵列和TDOA算法计算得到该局部放电源的空间三维坐标，并通过本文方法构建相机投影模型，实现了对该局部放电源的可视化标注。标注结果表明，半径为10 cm的圆形标注框所在的区域基本覆盖了局部放电所产生的区域，两次试验测试计算得到的交叠率分别为0.67和0.72，验证了标注方法的可行性以及标注结果的准确性。